手算BP神经网络
现在很多人都说,做it门槛很低,脑子灵活点,愿意去熬的,培训个几个月就可以,无非是调调函数而已。
确实,现在一些程序员的工作,调调函数掌握得好的话,也是能够胜任的。但是,想要更进一步,还得不断提升自己,努力理解各种算法结构。
(类)神经网络算法在深度学习等领域应用十分广泛。
而负反馈BP神经网络其中应用最多的一种,很多神经网络的算法都是在BP神经网络上进行优化的。所以,理解一下BP神经网络是很有必要的。
关于神经网络的知识请自行谷歌。
神经网络结构主要包括:输入层、隐藏层和输出层
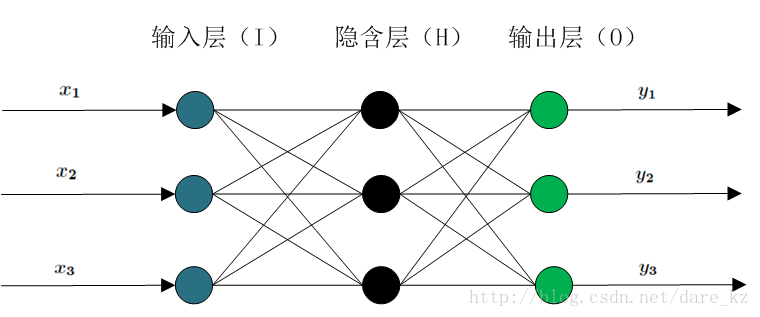
BP(Back Propagation)神经网络分为两个过程
(1)工作信号正向传递过程
(2)误差信号反向传递过程
工作信号正向传递过程(前向传播):
四个步骤:
1、输入层的每个节点,都要与的隐藏层每个节点做点对点的计算,计算的方法是加权求和+激活
2、利用隐藏层计算出的每个值,再用相同的方法,和输出层进行计算。
3、隐藏层用都是用Sigmoid作激活函数,而输出层用的是Purelin。这是因为Purelin可以保持之前任意范围的数值缩放,便于和样本值作比较,而Sigmoid的数值范围只能在0~1之间。
4、起初输入层的数值通过网络计算分别传播到隐藏层,再以相同的方式传播到输出层,最终的输出值和样本值作比较,计算出误差,这个过程叫前向传播(Forward Propagation)。
误差信号反向传递过程
两个步骤
BP算法是一种计算偏导数的有效方法,它的基本原理是:
5、利用前向传播最后输出的结果来计算误差的偏导数(前向传播后求偏导),
6、再用这个偏导数和前面的隐藏层进行加权求和
7、如此一层一层的向后传下去(隐藏层间偏导加权求和)
8、直到输入层(不计算输入层)(也就是第一隐藏层到输入层的偏导加权求和)
9、最后利用每个节点求出的偏导数来更新权重。
为了便于理解,后面一律用“残差(error term)”这个词来表示误差的偏导数。
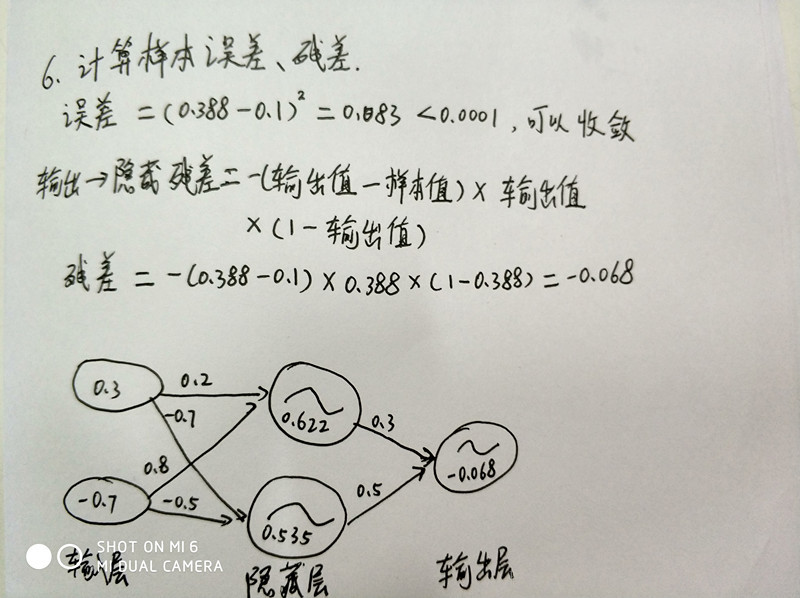
输出层→隐藏层:残差 = -(输出值-样本值) * 激活函数的导数
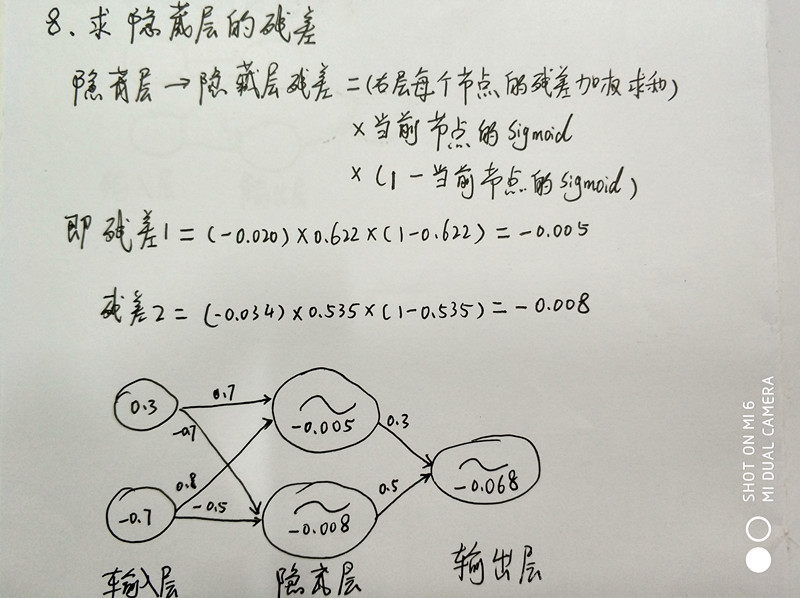
隐藏层→隐藏层:残差 = (右层每个节点的残差加权求和)* 激活函数的导数
如果用Sigmoid(logsig)作激活函数,那么:Sigmoid导数 = Sigmoid*(1-Sigmoid)
输出层→隐藏层:残差 = -(Sigmoid输出值-样本值) * Sigmoid*(1-Sigmoid) = -(输出值-样本值)输出值(1-输出值)
隐藏层→隐藏层:残差 = (右层每个节点的残差加权求和)* 当前节点的Sigmoid*(1-当前节点的Sigmoid)
残差全部计算好后,就可以更新权重了:
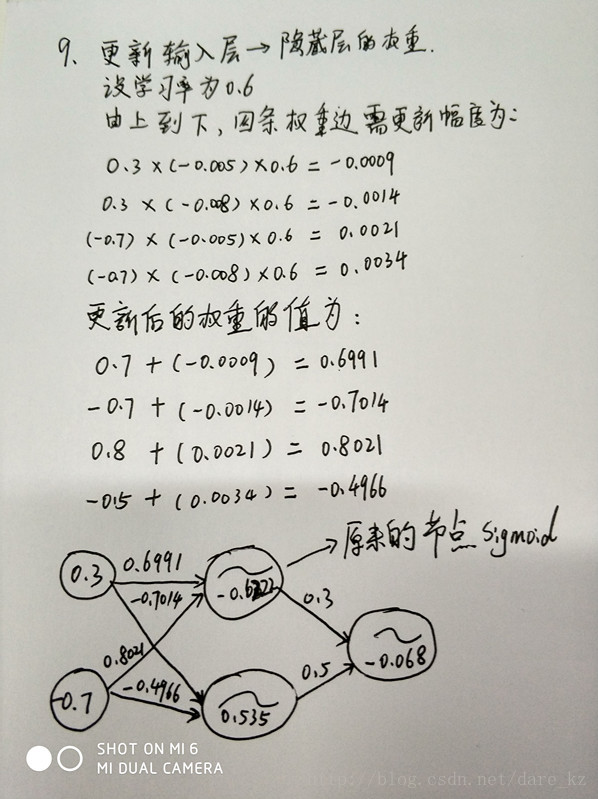
输入层:权重增加 = 输入值 * 右层对应节点的残差 * 学习率
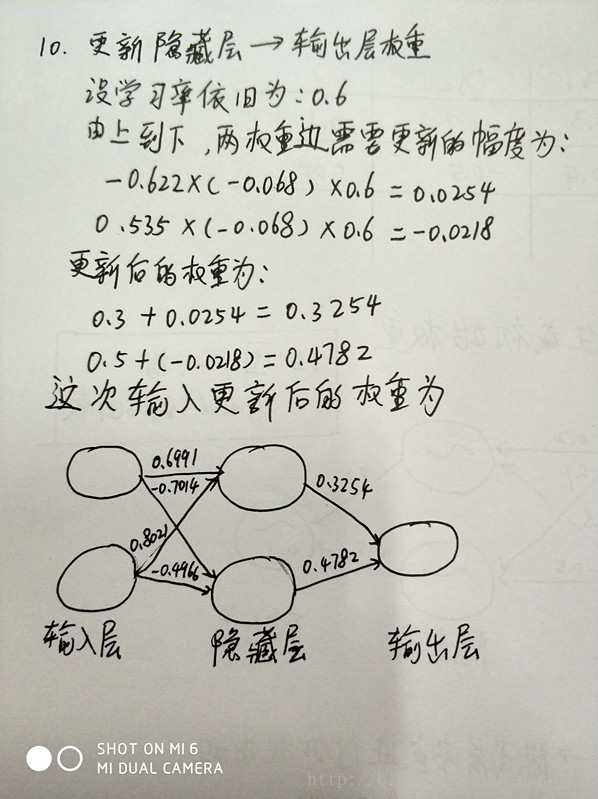
隐藏层:权重增加 = 当前节点的Sigmoid * 右层对应节点的残差 * 学习率
偏移值的权重增加 = 右层对应节点的残差 * 学习率
学习率是一个预先设置好的参数,用于控制每次更新的幅度。
此后,对全部数据都反复进行这样的计算,直到输出的误差达到一个很小的值为止。
以上介绍的是目前最常见的神经网络类型,称为前馈神经网络(FeedForward Neural Network),由于它一般是要向后传递误差的,所以也叫BP神经网络(Back Propagation Neural Network)。
文字的公式看上去有点绕,下面是一个详细的计算过程(非机器封包直接计算):
1、问题描述+随机生成初始权重
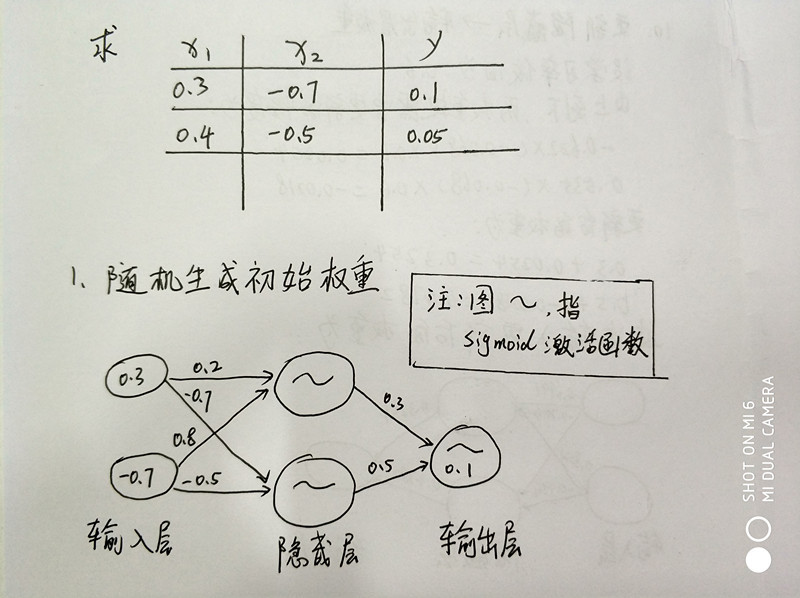
问题描述中,x1、x2 是神经网络的两个输入值,而y就是实际输出值
初始权重(层与层之间边的值),是一个(-1,1) 的随机数
可以通过Python 的random库获取
import random
print random.random()
print random.random()
print random.random()
print random.random()
print random.random()
print random.random()#结果
0.543717672492
0.0976781735159
0.373970033901
0.596229996543
0.741053525016
0.0915456485905
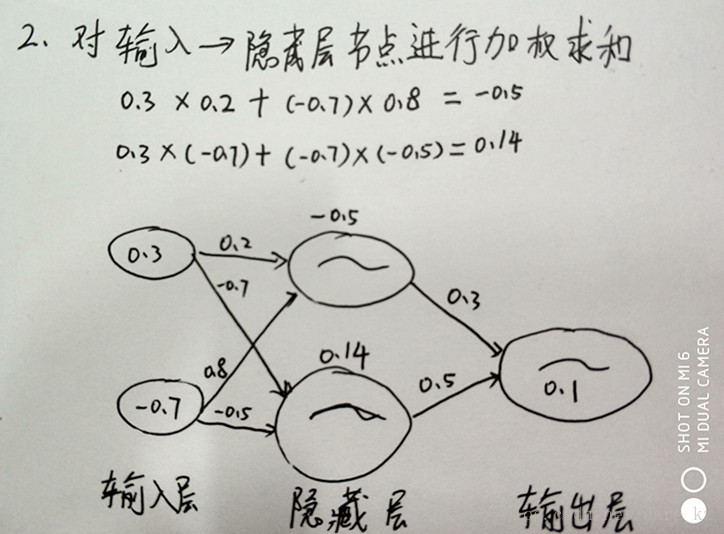
[Finished in 0.2s]2、对输入层 ->隐藏层节点进行加权求和
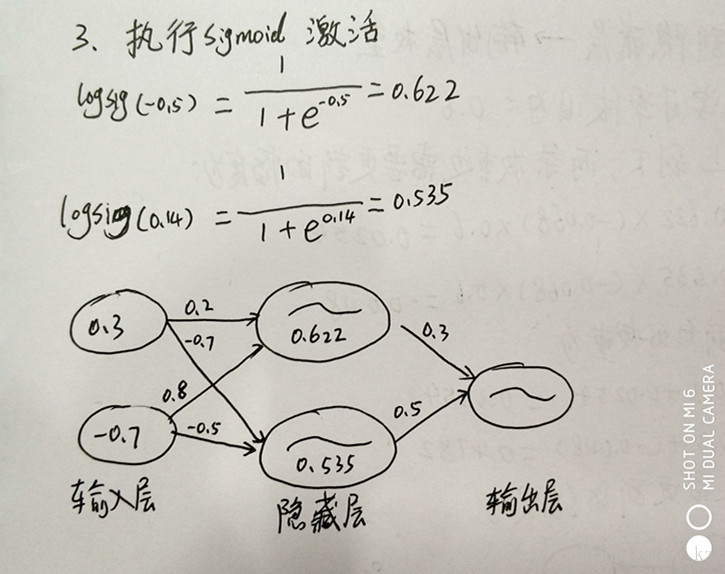
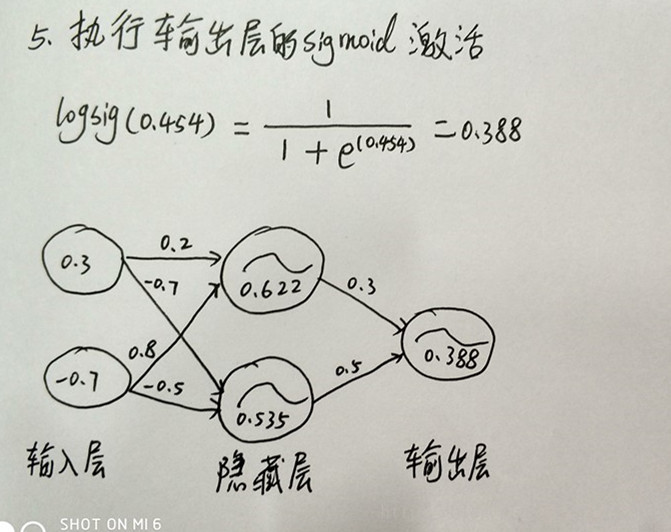
3、执行sigmoid激活
#这里的计算还是借助工具比较好
import math
print 1.0/(1+math.e**(-0.5))
print 1.0/(1+math.e**(-0.14))#结果
0.622459331202
0.534942945158
[Finished in 0.2s]4、对隐藏->输出层节点进行加权求和
5、执行输出层的sigmoid激活
6、计算样本的误差、残差
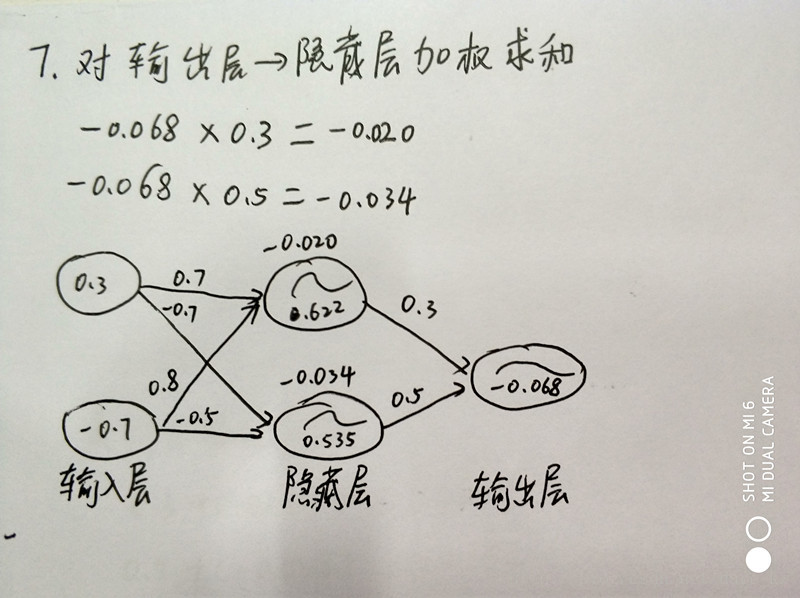
7、开始反向传播,对输出层-> 隐藏层加权求和
8、求隐藏层的残差
9、更新输入层 ->隐藏层的权重
10、更新 隐藏层->输出层的权重
至此,完成了一次的“学习”(也就是梯度下降)
后续就是一次次 往这个神经网络放进输入值和输出值,不断更新权重。
足够的学习次数之后,就是最终的结果。
有兴趣可以动手试试。

























 4879
4879

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








