三、特征值分布--盖尔圆、幂迭代

三、特征值分布–盖尔圆、幂迭代

1. 盖尔圆

列盖尔圆: A与AT的特征值相同，于是由A 的全体特征值都在 AT 的 n 个盖尔圆构成的并集中，同时称 AT 的盖尔圆为 A 的
连通盖尔圆： 相交的盖尔圆连通构成的区域，区域内有几个盖尔圆就有几个特征值

（1）盖尔圆特征值隔离—结合列盖尔圆

（2）盖尔圆特征值隔离—结合相似矩阵，特征值不变特性

选取对角阵：D = diag(d1, d2, · · · , dn)，其中di > 0 (i = 1, 2, · · · , n)，则A与B = D^-1AD相似且有相同特征值， 再隔离矩阵B特征值

• **如何选取对角阵D：**适当选取 D 的元素值，可以使 B 的某个圆盘半径相对减少。若要使 B 的第 i 个盖尔圆半径缩小，其余盖尔圆适量放大，可取di > 1，其他元素值取 1。增大孤立圆的半径，减小相交圆半径

特别注意复数矩阵盖尔圆表示：

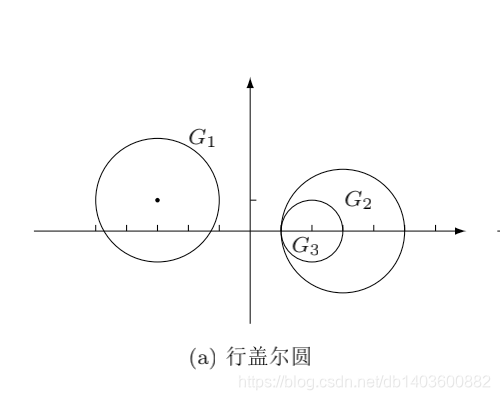
2. 幂迭代

五次或五次以上的多项式方程一般是没有公式求解的。所以对于阶数较大的矩阵，其特征值的计算是非常困难的，因而就要研究特征值的各种近似求法。仅要求得到矩阵的按模最大的特征值（或称为矩阵的主特征值）和相应的特征向量，如线幂迭代法（或简称幂法）就是解决此类问题的一种有效方法。