F1是合适的指标吗?那么F2 F3…F_beta呢?

使用F1分数进行二元分类的度量是很常见的。这就是所谓的调和均值。然而，更通用的F_beta评分标准可能更好地评估模型性能。那么F2 F3和F_beta呢?在这篇文章中，我们将回顾F指标。

介绍

根据许多数据科学家的说法，最可靠的模型性能度量是准确率。但是确定的模型指标不只有一个，还有很多其他指标。 例如，准确率可能很高，但是假阴性也很高。 另一个关键度量是当今机器学习中常见的F指标，用于评估模型性能。 它按比例结合了精度和召回率。 在这篇文章中，我们探讨了建议两者不平衡的不同方法。

混淆矩阵，精度和召回

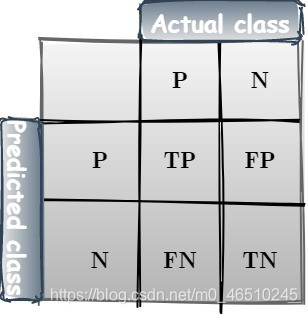
混淆矩阵总结了ML中有监督学习算法的性能。它比一般的精度度量提供了更详细的分析，因此更有益。在混淆矩阵中，每一行表示预测类中的实例，每一列表示实际类中的实例。简化后的混淆矩阵包含两行两列，如前所述，其中:

我们定义两个重要的度量:精度:TP样本的数量除以所有P样本(真和假)，召回:TP样本的数量除以(TP+FN)。

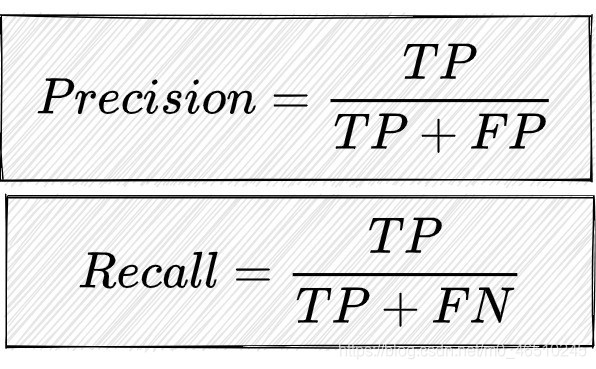
由于这两项措施都具有高度的重要性，因此需要一项措施将两者结合起来。因此，提出了精度和召回的调和均值，也称为F1分数。

F1分数

计算方式如下:

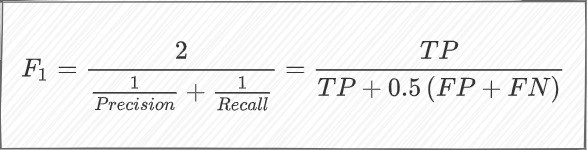
F1分数的主要优点(同时也是缺点)是召回和精度同样重要。在许多应用程序中，情况并非如此，应该使用一些权重来打破这种平衡假设。这种平衡假设可能适用于数据分布不均匀的情况，如大量正负数据。

F2和F3分数

使用加权平均值，我们可以很容易地得到F2分数:

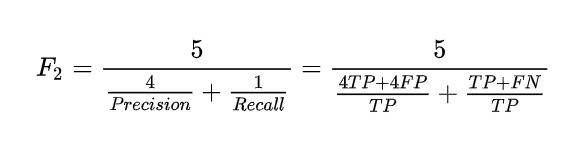
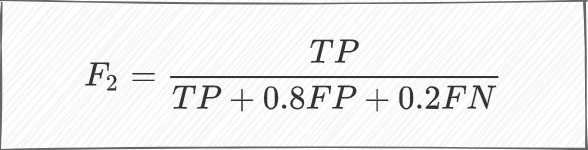
同样，F3得分为:

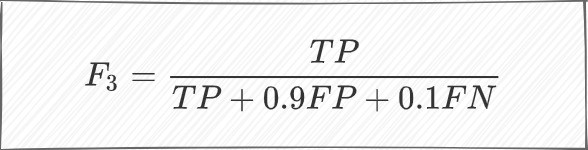
F_beta分数

推广加权平均法得到的F beta测度，由:

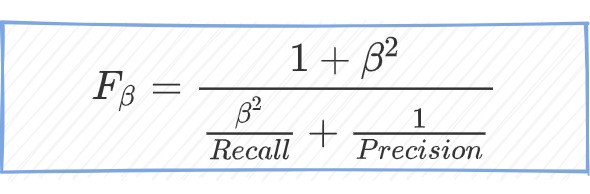
这种方法允许我们定义召回比精度重要多少。在sklearn中使用F beta度量非常简单，请查看以下例子:

>>> from sklearn.metrics import fbeta_score
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.23...
>>> fbeta_score(y_true, y_pred, average='micro', beta=0.5)
0.33...
>>> fbeta_score(y_true, y_pred, average='weighted', beta=0.5)
0.23...
>>> fbeta_score(y_true, y_pred, average=None, beta=0.5)
array([0.71..., 0.        , 0.        ])

总结

在这篇文章中，我回顾了F指标。我希望所提供的数据能够帮助那些处理分类任务的人，并帮助他们在使用准确性的同时使用F分数。

以下是·sklearn的文档，有兴趣的可以详细进行阅读：https://scikit-learn.org/stable/modules/generated/sklearn.metrics.fbeta_score.html?highlight=f%20beta#sklearn.metrics.fbeta_score

作者：Barak Or

deephub翻译组