1. 神经网络介绍
神经网络的原理根本在于对人类大脑行为的神经生物学模拟,这样看的话克隆技术也能算一种了吧。大脑可以看做一台精密、稳定、计算能力超强的计算机,其中的信息处理单元就是神经元(Neuron)。神经元是大脑处理信息的最小单元,它的结构如下图(再次使用了这个图):
Figure 1. 神经元结构
这个图抽象一下,由三部分组成:细胞体(Cell Body)、树突(Dendrite)、轴突(Axon)。名字都很形象,树突像一棵树那样伸展开来,这就是(这不就是赵老师说的:是你的末梢神经坏死,把上边给憋大了)。轴突长而细,我隐约记得某篇文章里好像曾说道轴突有2mm那么长,对于一个看不见的细胞体带着这样长的轴突,还是相对较长的。神经元之间就是通过这些树突和轴突连接进行信息交互。分工各不相同,树突的庞大组织作为神经元的输入,轴突则作为输出。一个神经元通过其庞大的树突结构从多个神经元处接受输入信号。同时它的轴突也会伸展向不同神经元输出信号。那神经元A的树突和另一个神经元B的轴突之间是如何实现信号传递的呢?这就引出下一个概念:突触(Synapse)。
Figure 2. 突触结构图
轴突/树突上的信号以电信号形式传输,突触在信号传递的过程中会把电信号转变成化学信号,然后通过突触间隙传递到下一个神经元的树突,再次转换成电信号,从而经历电信号-化学信号-电信号的转变过程。
介绍完输入输出,下面就是神经元的细胞体了。细胞体接收输入信号后,合成为一个输出,它的具体作用过程是我所不知的,但是后面在人工神经网络中可以看到用Sigmoid function来模拟它的处理过程。
这仅仅是一个信息处理单元,据估计大脑皮层拥有大约100亿神经细胞和60万亿的突触连接,这样的网络结构结果就是造就了大脑这样的高效组织。大脑的能效大约是
2. 人工神经网络(Artificial Neural Network)
2.1 神经元模型
现在用计算技术来模拟这样的网络,首先就是要实现一个神经元那样的处理单元。来看一下人造的神经元:
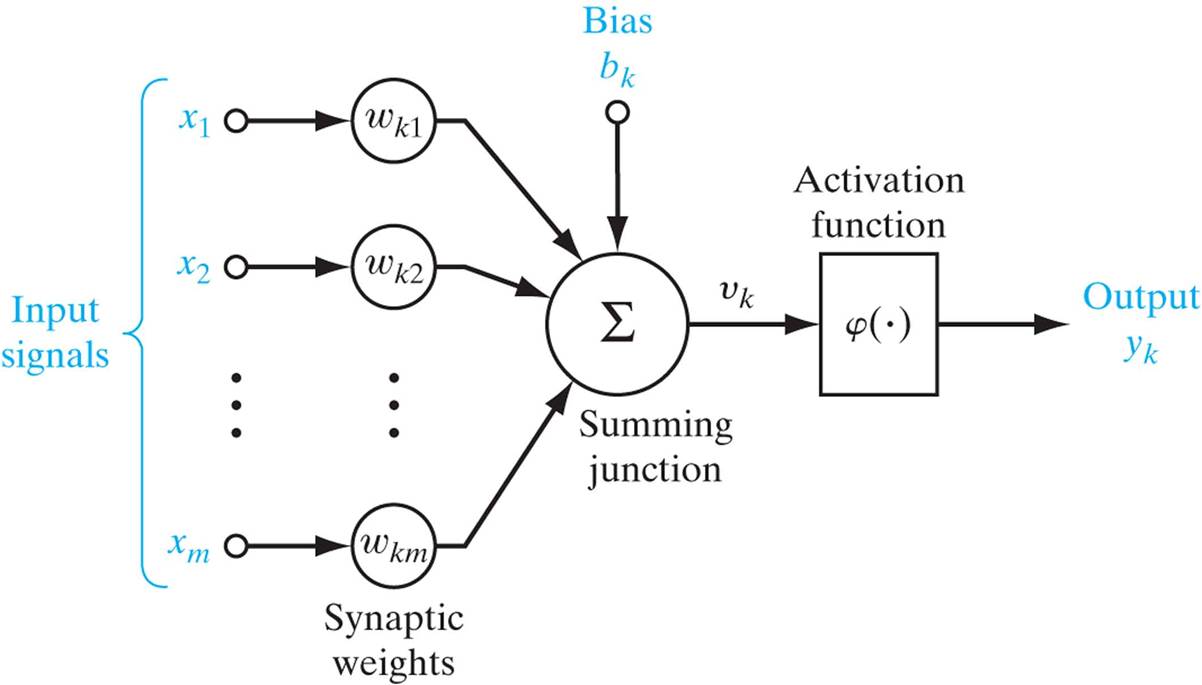
Figure 3.神经元模型
看过了前面的神经元,这个模型就不难理解是如何模拟的。同样,它也有多个(m)输入,突触以及树突上信号传递的过程被简化为加权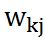
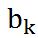
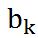
加法器的输出就是后面激活函数(Activation function)的输入范围,通过激活函数得到神经元的最终输出。激活函数有多种类型,最常见的就是Threshold函数和Sigmoid函数(前面提到过)。
Figure 4. (a) Threshold function; (b) Sigmoid function
形式分别为:Threshold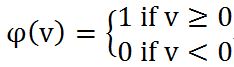
Sigmoid 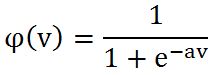
激活函数的作用是把输出压扁(squash)到一定范围内。以Sigmoid函数为例,输入从负无穷到正无穷,经过sigmoid函数映射到(0,1)范围,与Threshold函数不同的是它的连续性使得它的输出可以看做是结果等于1的概率。当v>0时输出为1;v<0时输出为0。这对应的是神经网络中神经元的两种状态:激活状态和未激活状态。
最后总结起来,神经元模型是一个对输入做Affine变换后经过激活函数的数学模型。
2.2 网络模型
人工神经网络是以层(layer)形式组织起来,包含一个输入层、一个输出层和一个或多个隐含层。每一层(除去输入层)中包含多个神经元,或者叫计算单元。输入层只是接收输入信号,并没有做计算。层与层之间通过神经连接(synaptic link)连接起来,如果神经元与前一层的每一个神经元之间都有连接(下图所示),这样的网络叫做全连接网络(completely-linked network),否则叫做部分连接网络(partially-linked network)。
Figure 5. 神经网络模型
这样的网络包含一个4个神经元的隐含层,一个2个神经元的输出层,一个包含10个输入节点的输入层。输入节点因为没有计算因为用方块表示,神经元用深色圆形表示。
2.3 模拟的能力
首先考虑一个神经元里的输出y与x之间的关系。激活函数的曲线在上面图4b中已经画出来,当输入由x变为ax时,曲线的平滑度将会随之变化:a越大函数曲线越陡,当a趋于正无穷时sigmoid函数逼近到Threshold函数。而如果输入由x变为x+b时,对曲线做平移。因而单个神经元是对输入的非线性映射。如图5中的网络模型,如果只有一个输入x,这个只包含一个隐含层的网络结构可以逼近x任意的非线性函数(隐含层神经元数目未必为4)。因而一个大型的全连接网络的模拟能力是可以想见的。
2.4 计算的能力
利用网络模型计算时,由输入层开始,每一个节点接收来自前一层中节点的输出,然后将计算结果传递到后面一层直到最后的输出层,叫做前向传播过程。
2.5 训练---BP
网络的训练目的就是要找到网络中各个突触连接的权重和偏置项。作为有监督学习的一种,它的训练过程是通过不断反馈当前网络计算结果与训练数据的label之间的误差来修正网络权重。当满足某个条件时退出训练。
首先取一个训练样例,输入经过初始化后的网络得到输出,然后计算输出与样例的desired output的误差,然后计算该误差对输出层输入的导数,再根据对输入层导数计算误差函数对隐含层-输出层权重的导数,根据此导数修正隐含层-输出层权重。继续这样的过程,计算误差函数对输入层-隐含层权重的导数,并修正输入层-隐含层权重……直到满足退出条件(误差精度或无调整),训练过程结束。
3. OpenCV中的神经网络
OpenCV中封装了类CvANN_MLP,因而神经网络利用很方便。
首先构建一个网络模型:
CvANN_MLP ann;
Mat structure(1,3,CV_32SC1);
structure.at<uchar>(0) = 10;
structure.at<uchar>(0) = 4;
structure.at<uchar>(0) = 2; // structure中表示每一层中神经元数目
ann.create(structure,CvANN_MLP::SIGMOID_SYM,1,1); // 很明显第二个参数选择的是激活函数的类型
然后需要对训练数据放在两个Mat结构中。第一个是存储训练数据的Mat train,第二个是存储类别的Mat label。其中,train的每一行代表一个训练样例,label的对应的一行是训练样例的类别。比如有25个属于7个类别的训练样例,每个样例为16维向量。则train结构为25*16,label结构为25*7。需要解释的是类别数据,label中一行表示样例所处类别,如果属于第一类则为(1,0,0,0,0,0,0),第二类为(0,1,0,0,0,0,0)...
接下来需要给ann提供一个样例的权重向量Mat weight,它标记的是训练样例的权重,这里都初始化为1:
Mat weight;
weight.ones(1,25,CV_32FC1);
接下来可以做训练了:
ann.train(train,label,weight);
训练结束后用ann来做分类,输入为Mat testSample,testSample为1*16的向量,输出为Mat output,output为1*7向量:
ann.predict(testSample,output);
最后找到output中的最大值就知道所属类别maxPos了:
int maxPos;
double maxVal;
minMaxLoc(output,0,&maxVal,0,&maxPos);
4. Game Over
THANK YOU !











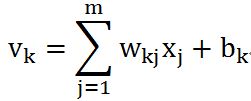















 2123
2123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








