用Opencascade生成和CATIA一样的B样条曲线

最新推荐文章于 2025-03-26 22:09:35 发布
最新推荐文章于 2025-03-26 22:09:35 发布
阅读量1.6k 收藏 10
点赞数
原文链接：http://www.cnblogs.com/apango/p/3440238.html
版权
本文详细解析了如何利用OCC实现与CATIA一致的B样条曲线，包括分析IGES格式、曲线参数，及OCC插值API的使用，确保了在造型设计中两者的精准对接。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目前采用OCC来实现造型，需要保证成形的结果和CATIA的结果一致。因此，首先要分析CATIA中形成的曲线具有什么样的参数，才能用OCC来做出一样的参数曲线来。这一次先用B样条来测试。

       

1. 首先分析IGES的格式，查阅IGES的标准规范。

  中国国家标准有对应的原始英文IGES标准的翻译版本：《GBT 14213-2008初始图形交换规范》或者英文好的直接看原版《Initial Graphics Exchange Specification, IGES 5.3》

IGES格式中，K+1代表控制点的个数，M代表基函数的阶数。按照NURBS的定义，设节点向量的个数为A+1，则有A=K+M+1。

在OCC中，定义L代表控制点个数，Degree代表基函数的阶数，控制点为FlatKnots。按照NURBS定义，有FlatKnots = L+Dgree+1。

二者本质是相同的，其中，FlatKnots=A+1，L=K+1。

下面是IGES参数数据段中，对应B样条线(126)的格式定义。

       

2. 分析CATIA保存的IGES的B样条曲线的参数。

     

下面以一个B样条曲线为例，来看看CATIA导出的IGES文件的具体内容。

设三个点坐标为A(1.0,0.0,0.0) B(0.0,0.0,0.0) C(0.0,1.0,1.0) ，按照A，B，C顺序插值获取一个样条线。

首先用CATIA生成该插值B样条曲线，两端的切矢分别为V1=(-0.959683,-0.198757,-0.198757), V2=(0.346512,0.663298,0.663298)。

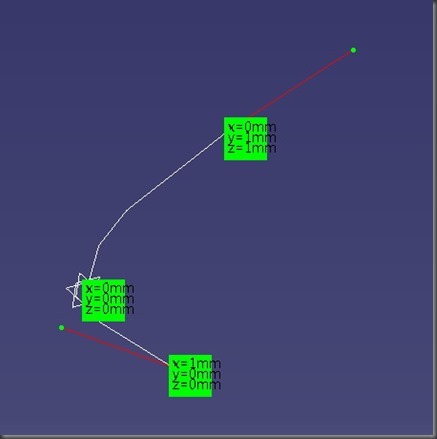
保存为IGES文件作为文本打开，其中样条的参数数据段如下，即7P对应的行。其中红色标记为B样条曲线的类型标记126，K=8，M=5。绿色为节点向量，紫色为权重，蓝色为控制点的坐标，三个一组。课件节点向量1.0对应的重度是3。如果直接插值为3次B样条（2阶连续曲线），该点的重度应该为1。

     

126,8,5,0,0,1,0,0.0,0.0,0.0,0.0,0.0,0.0,1.0,1.0,1.0,2.414213562,       7P      4
2.414213562,2.414213562,2.414213562,2.414213562,2.414213562,1.0,       7P      5
1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,0.0,0.0,0.7171572875,              7P      6
-0.05857864376,-0.05857864376,0.4757359313,-0.08786796564,             7P      7
-0.08786796564,0.2757359313,-0.08786796564,-0.08786796564,             7P      8
-0.1071067812,-0.01715728753,-0.01715728753,-0.2485281374,             7P      9
0.2242640687,0.2242640687,-0.2485281374,0.4242640687,                  7P     10
0.4242640687,-0.1656854249,0.6828427125,0.6828427125,                  7P     11
-6.898041511E-016,1.0,1.0,8.523144705E-018,2.414213562,0.0,0.0,        7P     12
0.0,0,0;                                                               7P     13

     

 转换为IGES标准中的定义表格形式：

索引

名称

数据

说明

1

K

8

K+1为控制点个数

2

M

5

阶数

3

PROP1

0

是否平面曲线

4

PROP2

0

是否闭曲线

5

PROP3

1

是否多项式

6

PROP4

0

是否周期

7

T(-M)

0.0

节点向量第一个

…

…

…

  

7+A

T(N+M)

2.414213562

节点向量最后一个

8+A

W(0)

1.0

权重第一个

…

…

…

  

8+A+K

W(K)

1.0

权重最后一个

9+A+K

X(0)

1.0

控制点第一个X

10+A+K

Y(0)

0.0

控制点第一个Y

11+A+K

Z(0)

0.0

控制点第一个Z

…

…

…

  

9+A+4*K

X(K)

-6.90E-16

控制点最后一个X

10+A+4*K

Y(K)

1.0

控制点最后一个Y

11+A+4*K

Z(K)

1.0

控制点最后一个Z

12+A+4*K

V(0)

8.52E-18

始参数值

13+A+4*K

V(1)

2.414213562

终参数值

14+A+4*K

XNORM

0.0

平面曲线的法向

15+A+4*K

YNORM

0.0

  

16+A+4*K

ZNORM

0.0

  

那么这样可以看出CATIA采用n=3个点插值出来的B样条曲线默认采用M=5阶的基函数，控制点的个数为3*n。那么n=3个点产生9个控制点。相应的节点向量数量为15。于是对应导出的IGES文件中K=8，M=5，A=14。

这个与NURBS BOOK中的插值算法有所不同，主要是参数u的初始化方法有所区别。NURBS BOOK中设置初始的u可以采用的主要有三种：

     

    a. 等间距equally space: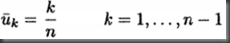

    b. 弦长chord length: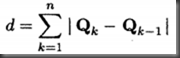然后

    c.  向心centripetal method: 然后

     

再仔细的观察，发现CATIA导出的曲线本质上是采用了第二种弦长法，其方法是在每一个控制点处重度提高到3（重度提高1阶，则连续性降低一阶），并升阶到5阶B样条。结合整体5阶的基函数，其实本质上相当于等效是采用3阶基函数B样条曲线（2阶连续）。将基函数从3阶升到5阶，从而曲线从2阶连续提高到4阶连续。然后各个控制点重度从1增加到3，使控制点处阶数降低2，曲线还是2阶连续。但是为什么CATIA需要这种方式来保存CAD数据，还有待思考。

       

3. 采用OCC实现相同参数的曲线并保存为IGES。

OCC可以采用GeomAPI提供的插值API：GeomAPI_Interpolate。也可以用BSplCLib提供的B样条底层算法来实现。建议使用API，会简单许多。 OCC中的GeomAPI_Interpolate插值出来的NURBS曲线为3阶，也就是2阶连续曲线，本质上和CATIA是相同的，只是CATIA升阶了。 GeomAPI插值的流程如下，每一步都不能跳过。

      a. 确定插值点，确定切矢约束

      b. GeomAPI_Interpolate()

      c. 用Load()添加约束

      d. 用Perform()进行插值

      e. 用IsDone()检查计算是否完成

      f. 用Curve()获得样条曲线对象

另外GeomAPI_Interpolate函数的参数中有两个要注意的地方：

一是插值点数组TColgp_HArray1OfPnt是一个可以自定义下标范围的类型，而在GeomAPI_Interpolate中要求这个参数的下标从1开始，而不是从0开始。（这个问题找的我吐血，看完插值源代码才明白）

二是Load()函数要求用两种方式给出切矢约束：每个点的切矢及其标致或者两端点的切矢。如果不需要切矢约束，可以采用前者，随意设置每一个点的切矢，之后设置所有点的标志为false。注意不能跨过Load()函数直接进行Perform()。

这样直接生成的B样条曲线为3阶（2阶连续），控制点5个。生成的IGES文件参数数据段如下：

     

126,4,3,1,0,1,0,0.E+000,0.E+000,0.E+000,0.E+000,1.,2.414213562,  0000001P0000001
2.414213562,2.414213562,2.414213562,1.,1.,1.,1.,1.,1.,0.E+000,   0000001P0000002
0.E+000,0.528595479,-9.763107294E-002,-9.763107294E-002,         0000001P0000003
-0.276142375,-9.763107294E-002,-9.763107294E-002,-0.276142375,   0000001P0000004
0.471404521,0.471404521,0.E+000,1.,1.,0.E+000,2.414213562,       0000001P0000005
-0.E+000,-0.707106781,0.707106781;                               0000001P0000006
S      1G      4D      2P      6                                        T0000001

     

颜色标记与之前的相同，红色标记为B样条曲线的类型标记126，K=4，M=3。绿色为节点向量，紫色为权重，蓝色为控制点的坐标。

此处发现了一个有趣的地方，这三个点插值获得曲线应该是平面曲线，但是CATIA没有将其标记为平面曲线（见IGES格式参数数据段索引编号为3的数据标记），并且最后一个控制的坐标没有精确为0.0，而是-6.898041511E-016。

为了进一步检验二者是否一致，将OCC生成的IGES导入CATIA，用CATIA的精确测量检查二者最大距离，最大距离结果当然是精确为0。

     

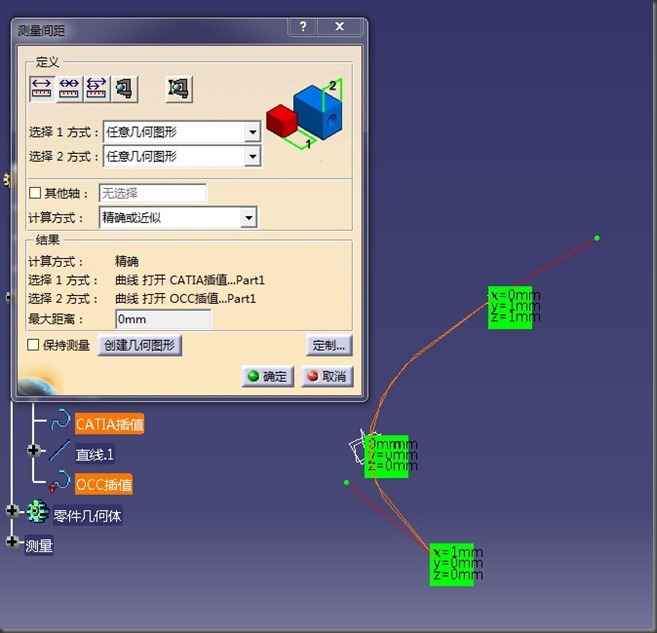
这样一来，就可以保证在曲线上，用OCC获取的曲线和CATIA获取的曲线精确一致了。但是等等，觉得还是不够？需要导出的阶数也完全一样？好吧，那么只需要进行升阶操作即可，以后再研究。

代码如下：

 

Handle(Geom_Curve) curve_test1()
{
    Handle(TColgp_HArray1OfPnt) pts = new TColgp_HArray1OfPnt(1,3);
    pts->SetValue(1,gp_Pnt(1.0,0.0,0.0));
    pts->SetValue(2,gp_Pnt(0.0,0.0,0.0));
    pts->SetValue(3,gp_Pnt(0.0,1.0,1.0));
    //define points to be interpolated
    GeomAPI_Interpolate interp(pts,Standard_False,1e-6);
    gp_Vec v(0.0,0.0,0.0);
    TColgp_Array1OfVec vtan(v,1,3);
    Handle(TColStd_HArray1OfBoolean) flags = new TColStd_HArray1OfBoolean(1,3,false);
    // define tangents and flags for every pole, any data is ok, not used.
    interp.Load(vtan,flags,Standard_False);
    interp.Perform();
    if ( interp.IsDone() )
    {
    // return curve with default degree
    // if you want to increase degree to 5, use this
    // (interp.Curve())->IncreaseDegree(5);
    return interp.Curve();
    }
    else                    
        return NULL;
}
     
void iges_write_test()
{
    IGESControl_Controller::Init();
    IGESControl_Writer ICW ("MM", 0);
    //creates a writer object for writing in Face mode with millimeters
    //Handle(Geom_Surface) surf = surface_test();
    Handle(Geom_Curve) curve = curve_test1();
    ICW.AddGeom (curve);
    //adds shape sh to IGES model
    ICW.ComputeModel();
    Standard_Boolean OK = ICW.Write ("MyCurveFile.igs");
    //writes a model to the file MyFile.igs                
}

 

 

 

这样导出来以后获得的IGES文件内容就和CATIA导出的一模一样了

     

126,8,5,1,0,1,0,0.E+000,0.E+000,0.E+000,0.E+000,0.E+000,0.E+000, 0000001P0000001
1.,1.,1.,2.414213562,2.414213562,2.414213562,2.414213562,        0000001P0000002
2.414213562,2.414213562,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,0.E+000,   0000001P0000003
0.E+000,0.717157288,-5.857864376E-002,-5.857864376E-002,         0000001P0000004
0.475735931,-8.786796564E-002,-8.786796564E-002,0.275735931,     0000001P0000005
-8.786796564E-002,-8.786796564E-002,-0.107106781,                0000001P0000006
-1.715728753E-002,-1.715728753E-002,-0.248528137,0.224264069,    0000001P0000007
0.224264069,-0.248528137,0.424264069,0.424264069,-0.165685425,   0000001P0000008
0.682842712,0.682842712,0.E+000,1.,1.,0.E+000,2.414213562,       0000001P0000009
-0.E+000,-0.707106781,0.707106781;                               0000001P0000010
S      1G      4D      2P     10                                        T0000001

     

和CATIA导出的IGES文件数据一样，绿色为节点向量，紫色为权重，蓝色为控制点的坐标，三个一组，节点向量1.0对应的重度是3。K=8，M=5，A=14。

转载于:https://www.cnblogs.com/apango/p/3440238.html

dengtan7279
关注
OpenCASCADE开发指南：专栏内容介绍及目录
欧特GO
03-15 5077
OpenCASCADE开发指南：专栏内容介绍及目录
OpenCASCADE绘制测试线束：几何命令之曲线创建
希望我的博客，能帮上你解决学习中工作中所遇到的问题
08-11 922
OpenCASCADE绘制测试线束：几何命令之曲线创建几何命令之曲线创建pointlinecircleellipsehyperbolaparabolabeziercurve, 2dbeziercurvebsplinecurve, 2dbsplinecurve, pbsplinecurve, 2dpbsplinecurveuiso, visoto3d, to2dproject 几何命令之曲线创建 本节涉及点和曲线。曲线类型有： 分析曲线，例如直线、圆、椭圆、抛物线和双曲线。 极坐标曲线，例如贝塞尔曲线和 bs
OpenCasCade与NURBS——B样条曲线
简单记录
08-04 8440
NURBS是非均匀有理B样条的简称，NURBS是现在通用CAD软件中比较高级的建模方法，B样条在创建曲线或曲面时有很高的灵活性，会用并善用基本上能获得想要的任意“自然”、光滑的曲线。 OpenCasCade是国外一款开源的CAD建模引擎，功能比较完备、强大。现在OpenCasCade母公司也以提供基于OpenCasCade的定制化CAD软件和服务为主要业务。 B样条曲线的分类 B样条曲线是B...
opencascade 线形成曲面 平移变换 opencascade 绘制样条曲线 gp_Ax1 opencascade 等数离散 等弦高离散
汤圆
04-23 344
opencascade 线形成曲面。
Open CASCADE学习|小球沿样条曲线运动
最新发布
T20151470的博客
03-26 384
动画的核心是通过不断更新球体的位置来实现的。我们通过一个循环逐步改变球体在样条曲线上的位置。在OpenCASCADE中，样条曲线（B样条曲线）是通过控制点来定义的。将样条曲线和球体添加到视图中进行显示。类来根据给定的控制点生成B样条曲线。按钮点击事件触发动画函数。
OpenCasCade(六) 曲线曲面
小胖七少爷的博客
09-05 3181
1.1B样条曲线 (1)GeomAPI_Interpolate：插值法生成BSpline曲线 例1：用插值法生成B样条曲线 OCGeomAPI_Interpolate PtB = new OCGeomAPI_Interpolate(HArray, false, OCPrecision.Approximation()); PtB.Perform(); OCGeom_BS...
opencascade绘制B样条插值曲线
ha0ha0xuexi的博客
06-03 2016
opencascade绘制B样条插值曲线 opencascade提供了B样条曲线曲面的绘制方法，涉及的类有 下面以绘制B样条插值曲线为例： QVector<gp_Pnt> points; points.push_back(gp_Pnt(0,0,1)); points.push_back(gp_Pnt(0,1,1)); points.push_back(gp_Pnt(1,2,1)); points.push_back(gp_Pnt(1,3,1)); int
均匀三次b样条曲线_opencascade 曲线入门
weixin_39748445的博客
11-27 802
转载，大佬的教程在这里OpenCASCADE几何曲线​mp.weixin.qq.comOCC曲线的基本用法#include<iostream> #include<Geom_Line.hxx> #include<Geom_Circle.hxx> #include<Geom_Ellipse.hxx> #include<Geom_Parabola....
SnappyHexMesh参数调优全解析：网格生成优化法
![SnappyHexMesh 网格生成教程](https://damogranlabs.com/wp-content/uploads/2018/05/mesh-impeller-1024x588.png) 参考资源链接：[Openfoam ...SnappyHexMesh是一个用于生成高质量六面体和四面体网格的程
开源CAD/CAE工具（FreeCAD）
weixin_43156294的博客
12-10 1915
FreeCAD是一个基于OpenCASCADE的开源CAD/CAE工具，可运行于Windows、Linux以及macOS系统环境下。它是一种通用的3D CAD建模软件，采用GPL和LGPL许可证开源。FreeCAD配备了现代化的3D CAD建模功能和许多2D元件，可用于绘制2D形状、提取三维模型的设计细节以创建2D生产图纸等，适用于机械工程、建筑及其他工程专业等广泛领域，并且具有类似CATIA、SolidWorks或Solid Edge的工具，能够提供CAX（CAD、CAM、CAE）、PLM等功能。
多年收集的一些稀有软件1
热门推荐
weixin_34080951的博客
10-06 1万+
QQ:365543212 PTC系列产品： PTC Creo 5.0.1.0+ HelpCenter Full Multilanguage Win64 2DVD PTC Creo 4.0.M050& HelpCenter Full Multilanguage Win64-ISO 2DVD PTC Creo 4.0.M020& HelpCenter Full Multi...
OpenGL - 连续绘制三次B样条曲线
wyg1997
10-19 9975
计算公式： 使用说明：鼠标在窗口点击绘制B样条曲线，鼠标右键移动控制点。退格键（←）删除鼠标所在的点。运行效果： 代码如下：#include<gl/glut.h> #include<math.h> #include<windows.h> #include<vector> #include<algorithm> using namespace std; bool mouseRightIsDown
Catia中如何取出曲线和曲面上点的坐标值
03-05
附图片和说明，非常详细。从Catia数据模中批量提升点的坐标值（曲面和曲线都试过，绝对可以用）！！！！
OpenCasCad (OCCT)几何数据：ModelingData
极客BIM工作室
11-20 1353
前言 从个人经验出发，对 OCCT 的几何表达和拓扑结构作了一下整理，不一定准确。 ModelingData 从 官方文档 中可以知道，ModelingData 这个模块包含四个部分： TKG2d：Toolkit Geometry 2D，即二维几何表达 TKG3d：Toolkit Geometry 3D，即三维几何表达 TKGeomBase：Toolkit Geometry Base，即几何基础 TKBRep：Toolkit Bourndary Representation TKG2d 二维几何表达
CATIA Automation 编程绘制样条曲线
独木专栏
04-02 5606
之前用 VC 编写了画圆的简单例子，今天试了一下绘制样条曲线的功能。 还是按照 Automation 的基本流程： 1 录制宏命令 Language="VBSCRIPT" Sub CATMain() Set partDocument1 = CATIA.ActiveDocument Set part1 = partDocument1.Part Set bod
第二章：Pythonocc官方demo 案例38（几何b样条曲线）
loujiand的博客
11-24 435
pythonocc 几何b样条曲线的建立。
B-样条曲线：开曲线
tuqu的专栏
03-13 1万+
B-样条曲线：开曲线B-spline Curves: Open Curves                                                                                                                    上一页定义               回目录                 
B-样条曲线教程（B-spline Curves Notes）目录
狼牙
03-22 7063
转载自：http://blog.csdn.net/tuqu/article/details/4749586   B-样条曲线教程 B-spline Curves Notes      本教程是关于B-样条曲线（B-spline Curves）的教程。B-样条曲线在计算机视觉(computer vision )，计算机图形学（Computer Graphics ），计算机辅助设计（Compu
Mesh Data Structure in OpenCascade
weixin_33938733的博客
04-08 870
Mesh Data Structure in OpenCascade eryar@163.com 摘要Abstract：本文对网格数据结构作简要介绍，并结合使用OpenCascade中的数据结构，将网格数据在OpenSceneGraph中可视化。 关键字KeyWords：OpenCascade、OpenSceneGraph、Triangulation、Mesh Data Structure...
opencascade曲线和曲面
02-18
### OpenCASCADE中曲线和曲面的基础知识 在OpenCASCADE技术中，曲线和曲面构成了几何建模的核心组件。曲线用于描述二维或三维空间内的路径，而曲面则由一系列曲线构成，在更复杂的空间内形成图形[^1]。 #### 创建基本曲线实例 对于创建简单的圆弧曲线，可以通过`Geom_Circle`类实现： ```cpp gp_Ax2 axis(gp_Pnt(0., 0., 0.), gp_Dir(0., 0., 1.)); Handle(Geom_Circle) circle = new Geom_Circle(axis, radius); ``` 上述代码片段展示了如何基于给定半径和轴向位置初始化一个圆形对象。 #### 构造与显示简单曲面 当涉及到构建较为复杂的形状时，则需要用到诸如贝塞尔曲面(`Geom_BezierSurface`)或是BSpline曲面(`Geom_BSplineSurface`)这样的高级结构。下面是一个利用四个控制点建立平面四边形的例子： ```cpp TColgp_Array2OfPnt poles(1, 2, 1, 2); // 定义角点坐标 poles.SetValue(1, 1, gp_Pnt(-width / 2, -height / 2, 0)); poles.SetValue(1, 2, gp_Pnt(width / 2, -height / 2, 0)); poles.SetValue(2, 1, gp_Pnt(-width / 2, height / 2, 0)); poles.SetValue(2, 2, gp_Pnt(width / 2, height / 2, 0)); Handle(Geom_BezierSurface) surface = new Geom_BezierSurface(poles); ``` 此段程序说明了怎样通过指定顶点来生成一片平坦的矩形区域。 #### 用户交互下的选择机制 为了支持用户界面中的互动操作——比如选取特定的对象（即点、线、面），需配置适当的选择模式，并借助AIS模块提供的接口完成实际的功能逻辑[^2]: ```cpp Handle(AIS_InteractiveContext) context; context->SetSelectedShape(shape); // shape代表要选中的实体 context->UpdateCurrentViewer(); ``` 这段脚本体现了设置选定状态以及刷新视图的过程。 #### 几何约束处理 针对二维环境里的边界条件设定，OpenCASCADE允许开发者定义内部/外部关系，这有助于解决某些类型的拓扑连接问题[^3]。 #### 曲线分割技巧 如果目标是对现有曲线实施切割动作，那么可以考虑采用参数化方式定位切分的位置，进而获取新的端点数据[^4]。 ```cpp Standard_Real uFirst, uLast; // 参数范围限定了待分割区间 curve->D0(uSplitPoint, P); // 获取对应u值处的点位信息 ``` 这里演示的是依据预设参数取得某一点坐标的办法。 #### 放样体构造法 最后提及到的一种常见造型手段叫做“放样”，它能够根据一组轮廓线生成连续变化形态的立体模型。具体来说就是沿着引导轨迹堆叠多个不同尺寸大小的截断片断，最终合成所需的物体外形[^5]。 ```cpp TopoDS_Shape result; BRepOffsetAPI_ThruSections builder(Standard_True /*isSolid*/, Standard_False /*isRuled*/); for (auto& section : sections) { TopoDS_Wire wire = BRepBuilderAPI_MakeWire(section).Wire(); builder.AddWire(wire); } result = builder.Shape(); ``` 以上示例解释了如何组合多条闭合路径以形成完整的实心体或壳状物。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值