矩阵三角分解法（LU分解）

        矩阵分解法是高斯消元法的变形，它的复杂度和高斯消元法一样都是O(n^3)，但是矩阵分解法在处理线性方程组系（具有相同的系数矩阵，但是右端项不同的方程组）时，运算比较方便。

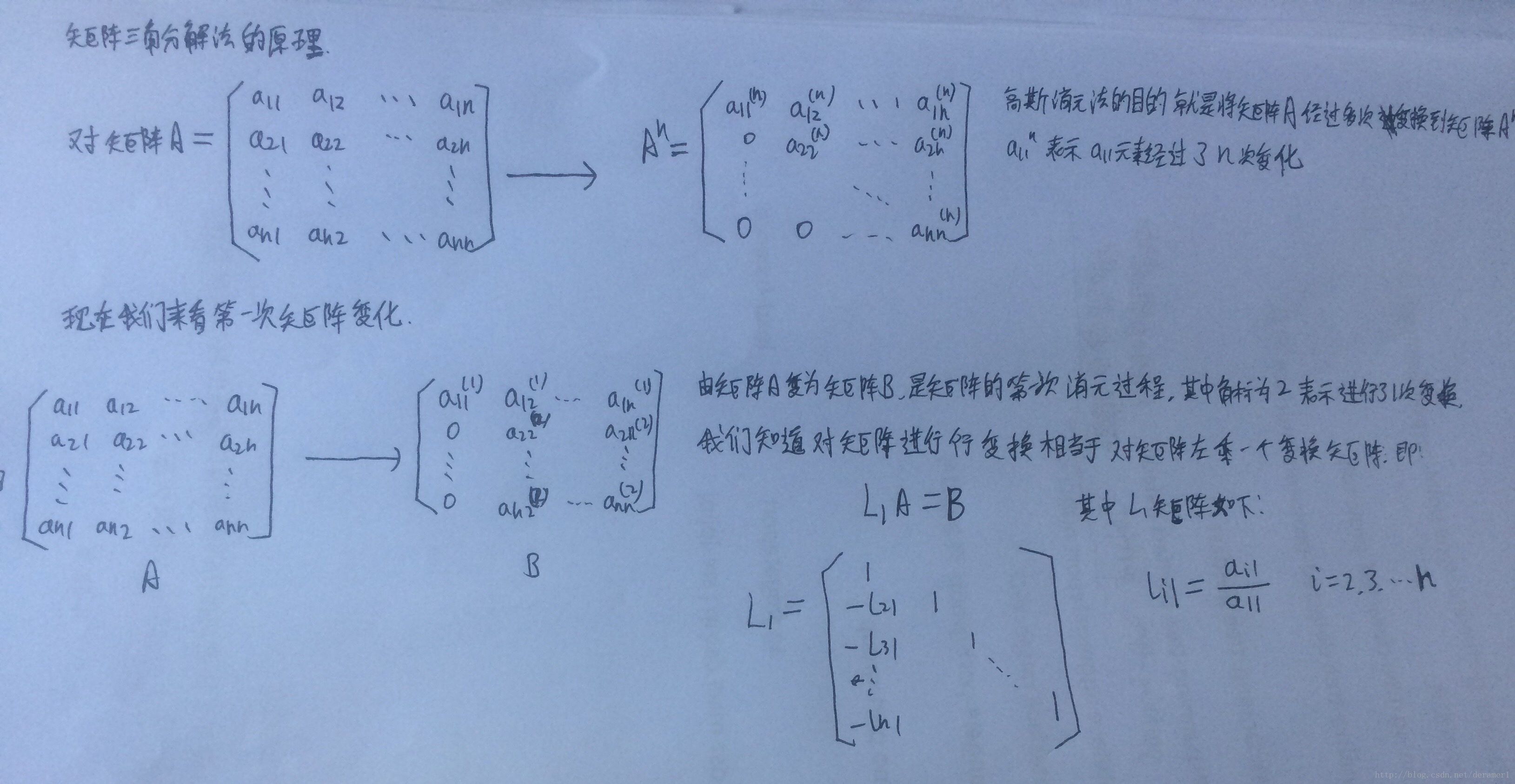
        下面是矩阵分解原理的原理：

   

    

   

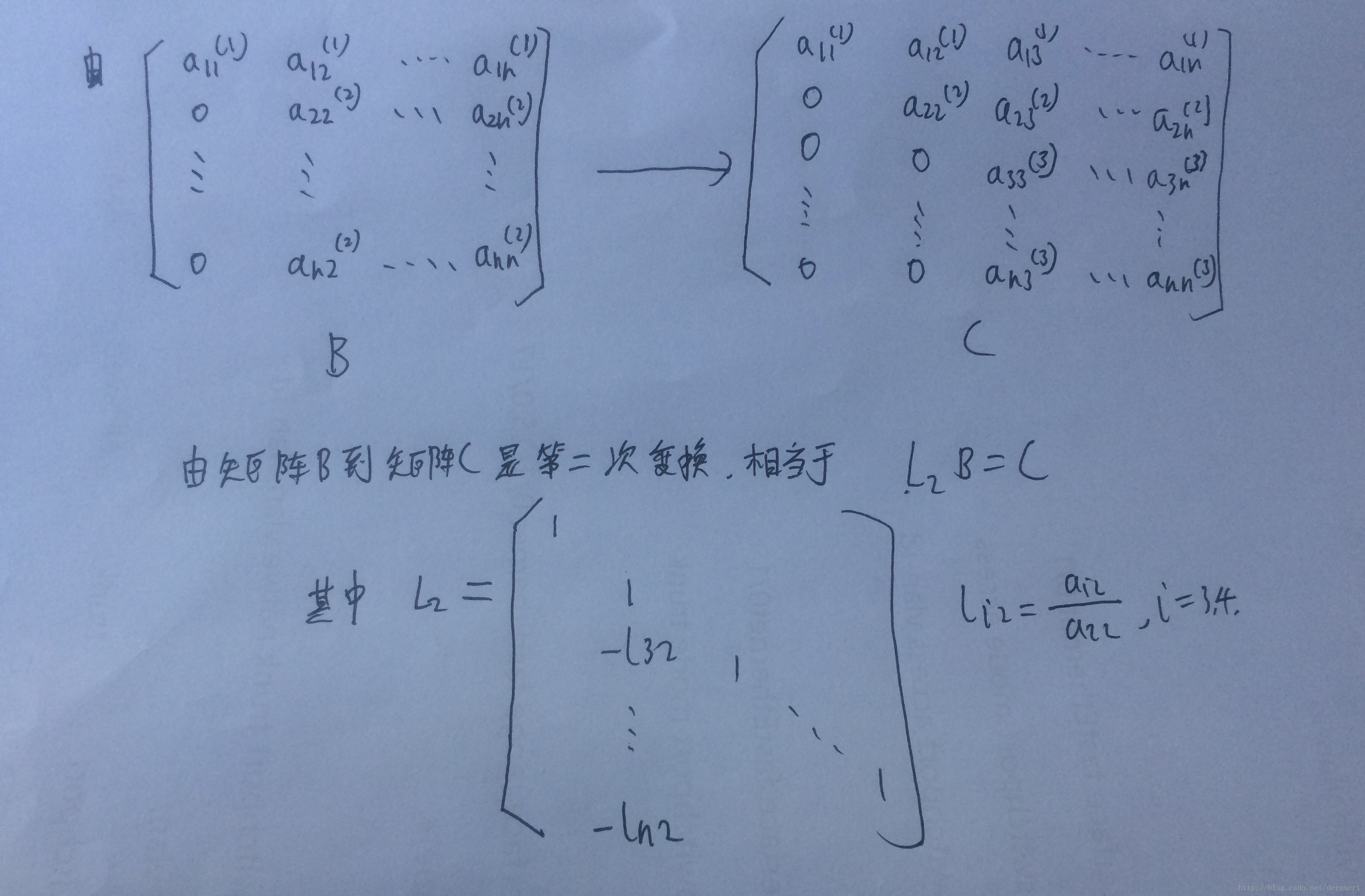
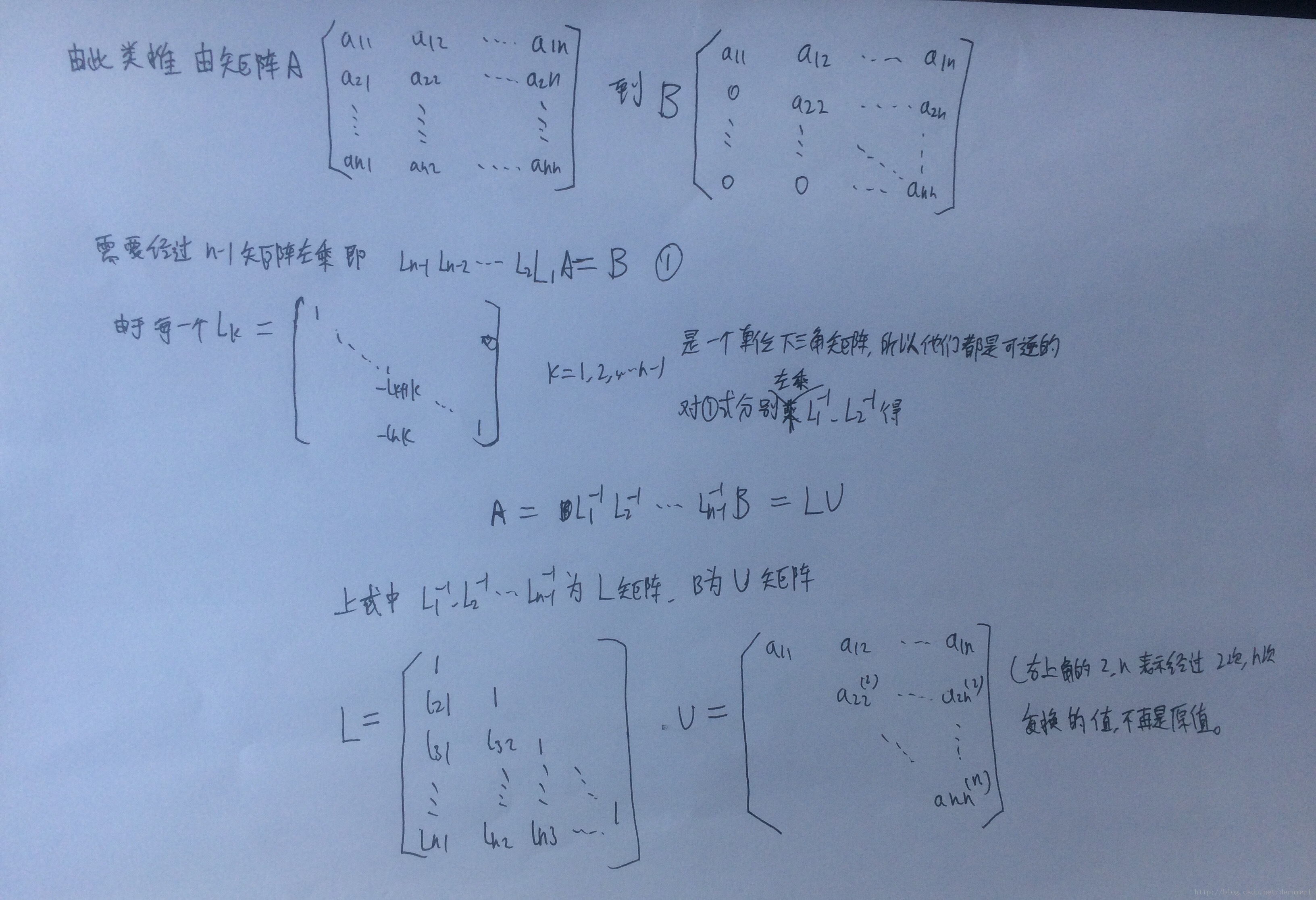
     下面是如何来求解L和U矩阵：

     

    在求L和U矩阵的时候，要注意两点：

   1>先求U矩阵中的一行，然后在求L矩阵的一列。次序不能颠倒。

   2>不论求L和U矩阵，都要用到相应的A矩阵中的数值。

   下面是求LU矩阵的python实现。

data = [[2, 2, 3], [4, 7, 7], [-2, 4, 5]]


#在实施LU分解的时候，所有的操作都在data矩阵上进行。因为LU分解的过程决定，它是一行一行进行分解的，所以用完的行可以被
#LU矩阵中的值所代替。
i = 0
size = len(data)
while i < size:
    if i == 0:
        j = 1
        while j < size:
            data[j][0]=data[j][0]/data[0][0]
            j += 1
    else:
        #下面是对U矩阵进行操作，操作过程是，先求一行U矩阵，后求一列L矩阵
        j = i
        while j < size:
            sum_column = 0
            flag_sum = i - 1
            while flag_sum >= 0:
                if j == i:
                    sum_column += data[flag_sum][j]*data[j][flag_sum]
                else:
                    sum_column += data[flag_sum][j]*data[j-1][flag_sum]
                flag_sum -= 1
            data[i][j] = data[i][j]-sum_column
            j += 1

        #下面的是对L矩阵进行操作，操作过程是求一列L矩阵
        m = i+1
        while m <size:
            sum_column_L=0
            flag_sum_L = i-1
            while flag_sum_L >= 0:
                sum_column_L += data[i][flag_sum_L]*data[m][flag_sum_L]
                flag_sum_L -= 1
            data[m][i] = (data[m][i]-sum_column_L)/data[i][i]
            m += 1
    i += 1


"输出LU矩阵"
L = []
U = []
l = 0
while l < size:
    r = 0
    temp=[]
    temp1=[]
    while r < size:
        if l > r:
            temp.append(data[l][r])
            temp1.append(0)
        else:
            if l == r:
                temp.append(1)
                temp1.append((data[l][r]))
            else:
                temp.append(0)
                temp1.append(data[l][r])
        r += 1
    L.append(temp)
    U.append(temp1)
    l += 1

print("L矩阵为：\n")
for x in L:
    print(x)
print("\n")

print("U矩阵为：\n")
for x in U:
    print(x)