一、原理
极大似然估计方法(Maximum Likelihood Estimate,MLE)也称为最大概似估计或最大似然估计,是求估计的一种方法。
给定一堆数据,假如我们知道它是从某一种分布中随机取出来的,可是我们并不知道这个分布具体的参数,即“模型已定,参数未知”。例如,我们知道这个分布是正态分布,但是不知道均值和方差;或者是二项分布,但是不知道均值。 最大似然估计就可以用来估计模型的参数。MLE的目标是找出一组参数,使得模型产生出观测数据的概率最大:
其中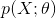
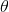
这一概率随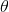
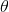

为了求导方便,一般对目标取log。所以最优化似然函数等同于最优化对数似然函数。
二、一般步骤
求极大似然函数估计值的一般步骤:
(1) 写出似然函数;
(2) 对似然函数取对数,并整理;
(3) 求导数;
(4) 解似然方程 。
三、例子
以《统计学习方法》(李航著)一书中求解二元逻辑斯谛回归模型为例(书79页)。
设:
似然函数为
对数似然函数为
对似然函数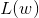

这样,问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯谛回归学习中通常采用的方法是梯度下降法及拟牛顿法优化似然函数。








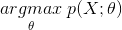
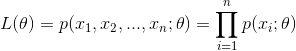
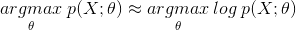

![\prod_{i=1}^{N}[\pi(x_{i})]^{y_{i}}[1-\pi(x_{i})]^{1-y_{i}}](https://img-blog.csdnimg.cn/20181227153150472)
![L(w)=\sum_{i=1}^{N}[y_{i}log\pi(x_{i})+(1-y_{i})log(1-\pi(x_{i}))]](https://img-blog.csdnimg.cn/20181227153150496)
![=\sum_{i=1}^{N}[y_{i}log\frac{\pi(x_{i})}{1-\pi(x_{i})}+log(1-\pi(x_{i}))]](https://img-blog.csdnimg.cn/20181227153150511)
![=\sum_{i=1}^{N}[y_{i}(w\cdot x_{i})-log(1+exp(w\cdot x_{i}))]](https://img-blog.csdnimg.cn/20181227153150527)













 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








