聚合标签算法简介

引言

聚合标签算法是由文献2提出的一种脉冲神经网络算法（SNN），该算法实际应用就是分类，而SNN算法按照分类方式，可以分为单脉冲学习算法和多脉冲学习算法。比如说需要进行手写体MNIST数字的分类，单脉冲学习算法就是通过构造一个有10个输出神经元的模型，将某张手写体数字转化为脉冲序列作为输入信号，当某个编号的输出神经元激发了一个脉冲同时其他的输出神经元保持沉默，那么该编号就是分类结果，比如tempotron学习算法[1]；同样，多脉冲学习算法同样构造有10个输出神经元的模型，将某张手写体数字转化为脉冲序列作为输入信号，其输出神经元连续输出n个脉冲（$n\in [1,2,\mathrm{3...}]，即输出的神经元数目可以不止取1$），那么输出神经元输出脉冲数目最多的一个即为识别结果，比如要介绍的聚合标签算法。

LIF神经元模型

依据实际神经系统，有众多神经元模型，该算法以LIF神经元模型为基础。我们直接给出其计算公式，其中$N$代表有N个输入神经元；$V_{rest}$表示静息电位，一般取0；${\omega }_i$表示第$i$个输入神经元与输出神经元连接的突触权重；$\theta$表示输出神经元脉冲激发阈值；$t_i^j$表示第i个输入神经元激发的第j个脉冲；$t$表示时刻；$t_{spike}^j$表示输出神经元激发的第j个脉冲；$V_{norm}$表示归一化常数，目标是使得$K(t-t_i^j)$范围在$[0,1]$内；${\tau }_m,{\tau }_s$分别是膜积分时间延迟常数，突触电流时间延迟常数;$V(t)$就是输出神经元膜电压。下面提到的计算输出膜电压过程全部是以这个公式为基础计算而来。

STS（Spike-Threshold-Surface）函数

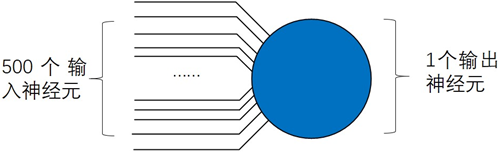
由于在SNN模型中神经元的输入输出信号全部是脉冲序列，脉冲序列的离散性导致无法直接求解关于权重的导数，从而不能更新权重，训练模型，于是聚合标签算法提出了一个STS函数和临界阈值$\theta$^*概念，为了更容易理解，我们构造了一个有500个输入神经元和1个输出神经元的两层网络。突触权重随机生成。

其输入的脉冲序列如下所示，其中横坐标代表了时间，纵坐标代表了1到500个输入神经元的编号，其中每一个黑色的点（x,y）代表了在x时刻第y个输入神经元激发了一个脉冲。

STS函数定义为对于同样的脉冲序列输入和突触权重一定时，不同输出神经元阈值与其激发的脉冲数目之间的映射关系，因为突触后神经元阈值越高，那么输出的脉冲数目越少，所以STS函数应该是一个单调递减的曲线，如下图即按照上面的两层网络和输入信号计算的STS函数图像。临界阈值$\theta$^*_k定义为输出脉冲数目从$k-1$增加到$k$时候的最大阈值。即下图中的拐点处，比如当突触后神经元阈值大于V_max时候，突触后神经元激发0个脉冲，但是当突触后神经元阈值等于V_max时候，突触后神经元激发了1个脉冲，所以$\theta$^*₁应该等于V_max

所以，临界阈值随着突触权重变化，输出脉冲数目随着临界阈值变化；最终将输出脉冲数目和突触权重的关系替代为临界阈值与突触权重之间的关系。

Multi-spike tempotron学习规则和基于临界阈值的梯度规则

引言

通过STS函数和临界阈值的定义，我们将离散的脉冲数目对权重的关系转化为临界阈值对权重之间的关系，那么接下来就需要训练模型，这就涉及到了Multi-spike tempotron学习规则和基于临界阈值的梯度规则，我们同样基于例子来介绍这两个规则，依旧是在上文中给出的两层神经网络模型和输入脉冲序列。此时，输出神经元激发的脉冲数目是3个，其输出神经元膜电压变化曲线如下所示。

我们希望通过更改突触权重后，使其可以激发6个脉冲。

multi-spike tempotron规则

Multi-spike tempotron规则就是如何更新权重。
$$\overrightarrow{\Delta }\omega =\{\begin{array}{rlr}& & -\lambda {\overrightarrow{\nabla }}_{\overrightarrow{\omega }}{\theta }_o^{\ast }\text{,if o > d}\\ & & \lambda {\overrightarrow{\nabla }}_{\overrightarrow{\omega }}{\theta }_{o+1}^{\ast }\text{,if o < d}\end{array}$$
其中$\lambda$是学习率，$o$表示实际输出神经元激发的脉冲数目，$d$代表预期输出神经元激发的脉冲数目，${\theta }_o^{\ast }$表示输出神经元激发脉冲数目为$o$的临界阈值，${\overrightarrow{\nabla }}_{\overrightarrow{\omega }}{\theta }_o^{\ast }$表示${\theta }_o^{\ast }$对突触权重（$\omega$是一个$1\times 500$的向量）的导数。
即当实际脉冲数目小于预期脉冲数目时候，希望增加突触权重，增大输出神经元膜电压和激发的脉冲数目，反之减少。

基于临界阈值的梯度规则

multi-spike tempotron规则给出了更新公式，临界阈值的梯度规则目的在于求解${\overrightarrow{\nabla }}_{\overrightarrow{\omega }}{\theta }_o^{\ast }$，求解过程可以具体参考论文的材料部分，反正是一个非常复杂的公式[2]。

更新权重

以输出6个脉冲为目标，训练上面的两层神经网络，更新权重后，可以得到输出神经元膜电压变化曲线如下图所示，

其中红色线为训练后的输出神经元膜电压变化，可以看到，其输出脉冲数目从3变成了6。
同时，STS函数曲线因为突触权重的改变，也随之发生了变化，其中黑色线为训练之前的STS函数，红色为训练后，黑色实线表示实际生物阈值，$\theta =1$，可以看到训练前${\theta }_4^{\ast }<\theta <{\theta }_3^{\ast }$，所以输出神经元激发3个脉冲，训练后${\theta }_7^{\ast }<\theta <{\theta }_6^{\ast }$，所以输出神经元激发6个脉冲。我们希望输出6个脉冲的目标可以理解为更新突触权重从而更新STS函数曲线，使实际生物阈值落到预期临界阈值范围之内。

[1]The tempotron: a neuron that learns spike timing–based decisions
[2]Spiking neurons can discover predictive features by aggregate-label learning