利用子集构造法实现NFA到DFA的转换

• 概述

NFA非有穷自动机，即当前状态识别某个转换条件后到达的后继状态不唯一，这种自动机不便机械实现，而DFA是确定有限状态的自动机，它的状态转换的条件是确定的，且状态数目往往少于NFA，所以DFA能够比较方便的机械实现且识别能力方面也和NFA相当。本次实验采用子集构造法来实现不带空弧的由NFA到DFA的转换。

 

子集构造法的算法如下：

设NFA为M=(K,Σ,f,S0,Z)，则构造相应的DFA  M′=(Q,Σ,f′,I0,F)
①取I0=S0；
②对于状态集Q中任一尚未标记的状态qi={Si1,Si2,…,Sim},Sik∈K，做：
 (1) 标记qi；
 (2) 对于每个a∈Σ，置
     T=f({Si1,Si2,…,Sim},a)
     qj=εCLOSURE(T)
 (3) 若qj不在Q中，则将qj作为一个未加标记的状态添加到Q中，且把状态转移f′(qi,a)=qj添加到M′。
③重复进行步骤②，直到Q中不再含有未标记的状态为止。对于由此构造的Q，我们把那些至少含有一个Z中的元素的qi作为M′的终态。

 

对于如图所示的NFA其在文件中保存的信息如下

 

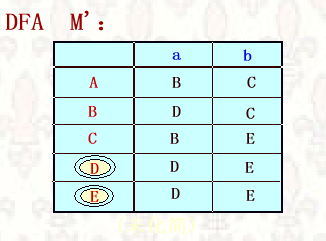
转成DFA之后的形式为

 

重命名为

• 程序整体思路

首先将文件中所给的NFA输入读入程序，在读入过程中将其以图的邻接表的形式保存，其中将状态转移条件记为该边的权值，每种状态记为图的结点，该状态识别状态转移条件(权值)之后到达的状态为该结点的邻接点。

 

对于上面的例子，将其读入程序中后该图在程序中的逻辑存储结构（图的邻接表）如图所示，其中邻接点中第一个数字表示权值，第二个数字表示所连的结点。

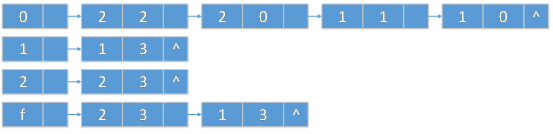
将图读入程序中后，再使用子集构造算法来完成由NFA到DFA的转化。

 

对于每种状态，其数据结构定义为

1 typedef struct state
2 {
3     set<int> Set;
4     char name;
5 }state;

View Code

其中set里存放该状态识别某个条件后所能到达的状态集合的下标，name里存该状态重命名后的名字。

 

这些状态保存在状态数组States[max]中，状态数组States[max]数据结构定义为

1 state S