SVM实现（简化版SMO）

最新推荐文章于 2023-12-04 16:34:11 发布
最新推荐文章于 2023-12-04 16:34:11 发布
阅读量283 收藏
点赞数
分类专栏： machine learning 文章标签： svm
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/diskdj/article/details/52597246
版权

以下是简化版SMO实现
SMO伪代码
创建alpha向量并初始化为0
迭代次数<最大迭代次数（外循环）
 循环每个数据向量（内循环）
  如果该向量违反KKT条件
   随机选取另一个向量
   优化两个向量
 如果所有向量都没被优化
  增加迭代次数，
 下一次迭代

# coding=utf-8
from numpy import *
import pylab as pl


class my_svm(object):
    def __init__(self, filename, c=6, tol=0.001, miter=30):
        self.filename = filename;
        self.C = c;
        self.tol = tol;
        self.miter = miter;
        self.support_vector = [];

    def loadDataSet(self):
        dataMat = [];
        labelMat = [];
        fr = open(self.filename);
        for line in fr.readlines():
            lineArr = line.strip().split('\t');
            dataMat.append([float(lineArr[0]), float(lineArr[1])]);
            labelMat.append(float(lineArr[2]));
        return mat(dataMat), mat(labelMat).transpose();

    def rand_select_j(self, i):
        j = i;
        while j == i:
            j = int(random.uniform(self.m));
        return j;

    def sample_svm(self):
        '''alphs*Y*<X,Xi>+b'''
        self.X, self.Y = self.loadDataSet();
        self.Y[self.Y == 0] = -1
        self.m, self.n = shape(self.X);
        self.alpha = mat(zeros((self.m, 1)));
        self.b = iter = 0;
        while iter < self.miter:
            alpha_change = 0;
            for i in range(self.m):
                '''求解Xi的预测值和误差'''
                Xi = float(multiply(self.alpha, self.Y).T * (self.X * self.X[i, :].T)) + self.b;
                err_i = Xi - float(self.Y[i]);

                '''违反KKT条件'''
                if (err_i * self.Y[i] < -self.tol and self.alpha[i] < self.C) or (
                                    err_i * self.Y[i] > self.tol and self.alpha[i] > 0):
                    '''随机选择另一个确定其误差，SMO的关键就是选择两个变量同时变化'''
                    j = self.rand_select_j(i);
                    Xj = float(multiply(self.alpha, self.Y).T * (self.X * self.X[j, :].T)) + self.b;
                    err_j = Xj - float(self.Y[j]);
                    alpha_i_old, alpha_j_old = self.alpha[i].copy(), self.alpha[j].copy();
                    '''求解H和L'''
                    if self.Y[i] == self.Y[j]:
                        L = float(max(0, self.alpha[i] + self.alpha[j] - self.C));
                        H = float(min(self.C, self.alpha[i] + self.alpha[j]));
                    else:
                        L = float(max(0, self.alpha[j] - self.alpha[i]));
                        H = float(min(self.C, self.C + self.alpha[j] - self.alpha[i]));
                    if L == H:
                        continue;
                    '''alpha的增量为：Y2*(err_1-err_2)/(K11+K22-2K12)统计学习方法上有详细的证明，其中K是核函数'''
                    eta = float(
                        self.X[i, :] * self.X[i, :].T + self.X[j, :] * self.X[j, :].T - 2.0 * self.X[i, :] * self.X[j,
                                                                                                             :].T);
                    if 0 == eta:
                        continue;
                    self.alpha[j] += self.Y[j] * (err_i - err_j) / eta;
                    '''根据限制条件：0<=alpha_j<=C,确定最终的alpha_j'''
                    if self.alpha[j] > H:
                        self.alpha[j] = H;
                    if self.alpha[j] < L:
                        self.alpha[j] = L;
                    # print("alpha[j]: ",float(alpha[j]),"alpha_j_old: ",float(alpha_j_old));
                    if (abs(float(self.alpha[j]) - float(alpha_j_old)) < 0.00001):
                        '''alpha的变化太小'''
                        # print("alpha的变化太小");
                        continue;
                    '''两个alpha变化大小相同'''
                    self.alpha[i] += self.Y[j] * self.Y[i] * (alpha_j_old - self.alpha[j]);
                    '''下面确定b，主要是通过新的alpha_i和alpha_j来确定b,主要运用两个公式'''
                    b1 = self.b - err_i - self.Y[i] * (self.alpha[i] - alpha_i_old) * self.X[i, :] * self.X[i, :].T - \
                         self.Y[j] * (self.alpha[j] - alpha_j_old) * self.X[i, :] * self.X[j, :].T
                    b2 = self.b - err_j - self.Y[i] * (self.alpha[i] - alpha_i_old) * self.X[i, :] * self.X[j, :].T - \
                         self.Y[j] * (self.alpha[j] - alpha_j_old) * self.X[j, :] * self.X[j, :].T
                    if (0 < self.alpha[i]) and (self.C > self.alpha[i]):
                        self.b = b1
                    elif (0 < self.alpha[j]) and (self.C > self.alpha[j]):
                        self.b = b2
                    else:
                        self.b = (b1 + b2) / 2.0
                    alpha_change = alpha_change + 1
                    print("iter: %d i:%d, pairs changed %d" % (iter, i, alpha_change))
            if (alpha_change == 0):
                iter += 1
            else:
                iter = 0
            print("iteration number: %d" % iter)
        self.__calculate_support_vector_and_weight_()

    def __calculate_support_vector_and_weight_(self):
        '''我们根据KKT条件给出支持向量，也就是alpha不等于0的项'''
        '''我们根据公式为：alpha*Y*X求解w'''
        self.w = zeros((self.n, 1));
        for i in range(self.m):
            if self.alpha[i]:
                self.support_vector.append([self.X[i].getA()[0][0], self.X[i].getA()[0][1]]);
                self.w += multiply(self.alpha[i] * self.Y[i], self.X[i, :].T);
        self.support_vector = mat(self.support_vector);

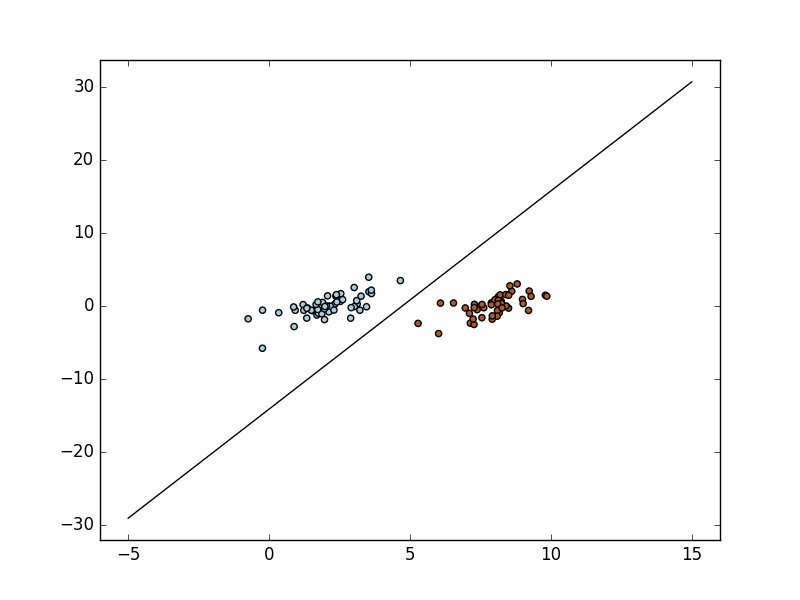
    def plot_svm(self):
        X = [];
        Y = [];
        fr = open(self.filename);
        for line in fr.readlines():
            lineArr = line.strip().split('\t');
            X.append([float(lineArr[0]), float(lineArr[1])]);
            Y.append(float(lineArr[2]));
        X = mat(X);
        a = -self.w[0] / self.w[1];
        XX = linspace(-5, 15);
        YY = a * XX - (self.b[0].getA()[0]) / self.w[1];
        pl.plot(XX, YY, 'k-');
        pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired);
        pl.axis('tight');
        pl.show();


svm = my_svm(filename='data/testSet.txt')
svm.sample_svm()
svm.plot_svm()

这里写图片描述

引入核函数

   def kernelTrans(self, X, A):  # calc the kernel or transform data to a higher dimensional space
        m, n = shape(X)
        K = mat(zeros((m, 1)))
        if self.kTup[0] == 'lin':
            K = X * A.T  # linear kernel
        elif self.kTup[0] == 'rbf':
            for j in range(m):
                deltaRow = X[j, :] - A
                K[j] = deltaRow * deltaRow.T
            K = exp(K / (-1 * self.kTup[1] ** 2))  # divide in NumPy is element-wise not matrix like Matlab
        else:
            raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
        return K

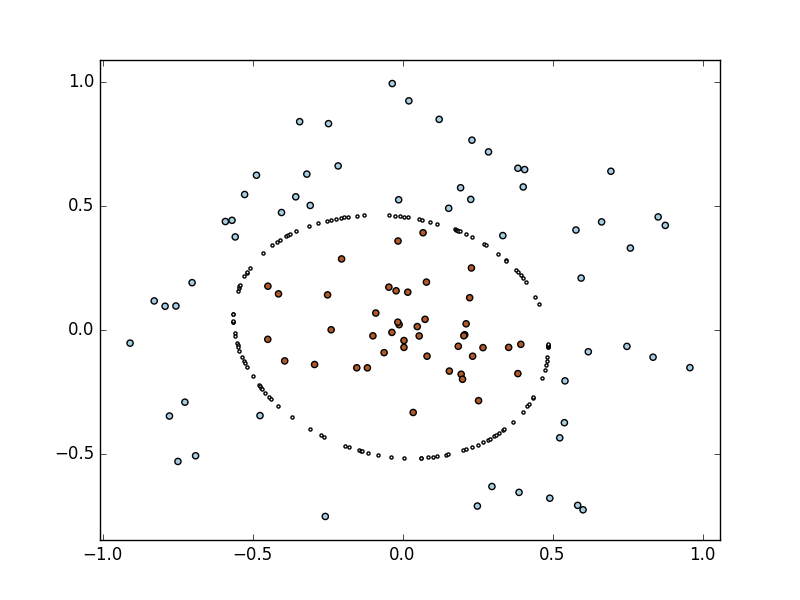
这里写图片描述

画出分界线

        XX = arange(-1, 1, linespace);
        YY = arange(-1, 1, linespace);

        for i in XX:
            for j in YY:
                Xi = float(multiply(self.alpha, self.Y).T * self.kernelTrans(self.X, [i, j])) \
                     + self.b;
                if (abs(Xi) < self.tol):
                    pl.scatter(i, j, c='w', s=5)

代码比较鸡肋，主要是用于学习，希望有志同道合的朋友能给予指点

QIN_08
关注
专栏目录
采用SMO优化算法训练SVM（实战篇）
GG_freedom
04-10 4288
算法笔记更新~ 引入   SVM（支持向量机），相信有一些机器学习基础的朋友对这个算法应该早已耳熟。SVM是现有的机器学习基础算法里较为能扛的一个。此篇文章偏向实战，对svm背后繁杂而又精致的数学知识不做展开叙述，在这一方面，笔者在学习时参考的是东大一位教授的知乎文章：零基础学习SVM，教授讲解的十分详细，引人入胜。层层递进的同时令人不禁感慨数学的美妙！如果你对svm最后的目标函数一无所知，同时又有兴趣探个究竟，强烈安利你移步上述链接。 SVM经过一番推导之后，得到的目标函数为: 对这个优化目标函数，解
支持向量机SVM与SMO算法的的详细推导过程
吊车尾小队
06-04 843
通俗来说，支持向量机就是一个二分类问题，根据所给的训练集数据集进行将数据的最佳划分，以达到测试集的最佳分类。支持向量机也叫做SVM，在实际工业的运用中，有着很强的可靠性和广泛的使用。接下来我们就来具体介绍一下这么好用的算法。所谓的二分类问题就是通过一条分割线来对数据进行分类，在二维情况下就是平面直角坐标系下的y=kx+b，当x的维度（对应与需要分类的条件，即属性增多的情况）大于等于2时，情况就上升的多维的情况，我们就引出了超平面的概念。
SVM的简单实现
10-19
机器学习SVM算法的简单实现。适用于初学者，使用python语言。
SVM算法的简单实现-sklearn
Data _designer
11-29 1461
#!/usr/bin/env python # coding: utf-8 # In[1]: #线性支持向量机的分类 import numpy as np from sklearn import datasets from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler fr...
python实现SMO（简化版）
啊李
06-26 1513
#来自周志华的《机器学习》import numpy as np from numpy import * #载入数据 def loadData(filename): dataMat = [] labelsMat = [] with open(filename) as fr: for line in fr.readlines(): lin...
【读书笔记】机器学习实战 6.3节 SVM-简化版SMO算法
xiaxzhou的博客
05-12 2304
机器学习实战 6.3节 支持向量机SVM 简化版SMO算法
【机器学习算法-python实现】svm支持向量机(2)—简化版SMO算法
Garvin的专栏
05-04 4196
(转载请注明出处：http://blog.csdn.net/buptgshengod) 1.背景知识       通过上一节我们通过引入拉格朗日乗子得到支持向量机变形公式。详细变法可以参考这位大神的博客——地址   参照拉格朗日公式F(x1,x2,...λ)=f(x1,x2,...)-λg(x1,x2...)。我们把上面的式子变型为：  约束条件就变成了：
SVM在MATLAB的实现——SMO
06-05
在MATLAB中，SVM的实现通常涉及到多种算法，其中包括简化的SMO（Sequential Minimal Optimization）算法。 SMO算法是由John Platt提出的，它是一种有效解决SVM优化问题的迭代方法。该算法的核心思想是每次迭代中只...
smo算法matlab实现,SVM之序列最小最优化算法（SMO算法）
weixin_33648352的博客
03-27 1582
SVM回顾支持向量机(SVM)的一大特点是最大化间距(max margin)。对于如上图的二分类问题，虽然有很多线可以将左右两部分分开，但是只有中间的红线效果是最好的，因为它的可活动范围(margin)是最大的，从直观上来说很好理解。对于线性二分类问题，假设分类面为$$\begin{equation} u=\vec w \cdot \vec x-b \end{equation}$$则margin为...
Smo算法简化版java代码
07-04
在这个“Smo算法简化版java代码”项目中，我们可以期待看到以下几点内容： 1. **SVM基本概念**：项目应该会介绍SVM的基本原理，包括最大间隔、支持向量和核函数等概念。在Java实现中，这些概念会体现在算法的各个...
SVM超简洁讲解拒绝长篇大论
justorderman的博客
05-03 928
一、SVM基本形式 1、线性可分 在二维空间上，两类点被一条直线完全分开叫做线性可分。 2、最大间隔超平面 从二维扩展到多维空间中时，将 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-irOQyuZ7-1620038837467)(https://www.zhihu.com/equation?tex=D_0)] 就成了一个超平面。 为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。 两类样本分别分割在该超平面的两侧.
SVM的实现
zju2016的博客
04-03 373
思路：从训练集当中选取一部分作为验证集，对于剩下的训练集，进行多次迭代，每次使用一定量的样本进行训练，用验证集进行测试，从而确定好超参数。确定了超参数之后，用所有的训练集开始进行训练，思路和之前的类似，迭代一定的次数，每次选取一定量的数据进行训练。在训练结束之后，利用测试集进行测试即可，具体实现见如下代码，准确率基本稳定在35%左右，比knn的方法要好。import numpy as np impo
SVM基本实现看这一篇就够啦
最新发布
qq_60891563的博客
12-04 753
在学SVM的时候前后看到了许多实现的办法，其中用梯度下降的办法算是比较好理解的，其中用拉格朗日乘子法求解的并没有搞的很懂，只推导到了下面这一步。然后得出了KKT的条件，就不知道怎么往下了。求大佬教教😍😍😍。
简化版SMO算法Scala实现
日渐学习
03-25 742
简化版SMO算法, 主要从Python机器学习实战里面转换过来, 风格比较命令式, 大量的var变量
机器学习知识总结 —— 16.如何实现一个简单的SVM算法
老程的技术笔记
01-18 1261
此外，如果需要对不平衡的数据进行分类，那么可能需要使用更高级的方法来调整损失函数。例如，对于少数类别，可以使用不同的权重来调整损失函数。如果需要对高维数据进行分类，那么可能需要使用核技巧来解决该问题。在这种情况下，可以使用高斯核函数代替线性核函数。如果需要对大规模的数据进行分类，那么可能需要使用分布式计算来解决该问题。在这种情况下，可以使用类似于Apache Spark或Hadoop之类的工具来处理数据。
支持向量机 （SMO算法原理与简化版实现）
troysps的博客
05-29 2529
SMO算法原理及实现 支持向量机的学习问题本质上是求解凸二次规划问题 SMO算法 序列最小最优化算法就是求解该问题的代表性算法 SMO算法 解决的凸二次规划的对偶问题: mina12∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαimina12∑i=1N∑j=1NαiαjyiyjK(xi,xj)−∑i=1Nαi\min\limits_{a} \frac{1}{2} \su...
SVM通俗详解
热门推荐
WGS.
07-08 8万+
SVM，英文全称为 Support Vector Machine，中文名为支持向量机，由数学家Vapnik等人早在1963年提出。在深度学习兴起之前，SVM一度风光无限，是机器学习近几十年来最为经典的，也是最受欢迎的分类方法之一。 1 SVM与“三八线” 不少人在初识SVM时会感觉到高深难懂。现在，就从你我熟知的“三八线”来走进SVM的思想内涵。 回忆下小时候，同桌同学经常会用粉笔或是小刀在课桌中间划一条“三八线”将课桌一分为二。大家约定好每个人只能在自己的那半课桌领域活动，谁也不能越界，越界是小猪、小狗。
手把手教你实现SVM算法（一）
weixin_30685047的博客
12-31 1836
什么是机器学习 （Machine Learning） 机器学习是研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域。 机器学习的大致分类： 1）分类（模式识别）：要求系统依据已知的分类知识对输入的未知模式（该模式的描述）作分析，以确定输入模...
支持向量机简化的SMO算法详解
"支持向量机(SVM)优化算法的简化版——SMO算法实现详解" ...尽管简化版SMO算法在某些场景下可能不够完善，但它可以帮助我们更好地理解和实现SVM的基本优化逻辑。对于实际应用，理解并掌握完整的SMO算法是非常重要的。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值