各种数据结构优缺点分析

原文地址：http://www.xuebuyuan.com/2218977.html

数组

优点：插入块如果知道坐标可以快速去地存取

缺点：查找慢,删除慢,大小固定

有序数组

优点：比无序数组查找快

缺点：删除和插入慢，大小固定

栈

优点：提供后进先出的存取方式

缺点：存取其他项很慢

队列

优点：提供先进先出的存取方式

缺点：存取其他项都很慢

链表

优点：插入快，删除快

缺点：查找慢

二叉树

优点：查找，插入，删除都快（如果数保持平衡）

缺点：删除算法复杂

红-黑树

优点：查找，插入，删除都快，树总是平衡的

缺点：算法复杂

 

2-3-4树

优点：查找，插入，删除都快，树总是平衡的。类似的树对磁盘存储有用

缺点：算法复杂

 

哈希表

优点：如果关键字已知则存取速度极快，插入块

缺点：删除慢，如果不知道关键则存取很慢，对存储空间使用不充分

堆

优点：插入，删除块，对最大数据的项存取很快

    缺点：对其他数据项存取很慢

图

优点：对现实世界建模

缺点：有些算法慢且复杂

 

 

http://www.cppblog.com/cxiaojia/archive/2012/08/06/186432.html

二叉树首先是一棵树，每个节点都不能有多于两个的儿子，也就是树的度不能超过2。二叉树的两个儿子分别称为“左儿子”和“右儿子”，次序不能颠倒。

一种是满二叉树，除了最后一层的叶子节点外，每一层的节点都必须有两个儿子节点。

另一种是完全二叉树，一棵二叉树去掉最后一层后剩下的节点组成的树为满二叉树，最后一层的节点从左到右连续，没有空出的节点，这样的树称为完全二叉树。

 

http://blog.csdn.net/v_JULY_v/article/details/6105630

二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点（no duplicate nodes）。

平衡树是计算机科学中的一类数据结构。
平衡树是计算机科学中的一类改进的二叉查找树。一般的二叉查找树的查询复杂度是跟目标结点到树根的距离（即深度）有关，因此当结点的深度普遍较大时，查询的均摊复杂度会上升，为了更高效的查询，平衡树应运而生了。

几乎所有平衡树的操作都基于树旋转操作，通过旋转操作可以使得树趋于平衡。 对一棵查找树（search tree）进行查询/新增/删除 等动作, 所花的时间与树的高度h 成比例, 并不与树的容量 n 成比例。如果可以让树维持矮矮胖胖的好身材, 也就是让h维持在O(lg n)左右, 完成上述工作就很省时间。能够一直维持好身材,
不因新增删除而长歪的搜寻树, 叫做balanced search tree（平衡树）。

而红黑树，能保证在最坏情况下，基本的动态几何操作的时间均为O（lgn）。

ok，我们知道，红黑树上每个结点内含五个域，color，key，left，right，p。如果相应的指针域没有，则设为NIL。

一般的，红黑树，满足以下性质，即只有满足以下全部性质的树，我们才称之为红黑树：

1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。

（注：上述第3、5点性质中所说的NULL结点，包括wikipedia.算法导论上所认为的叶子结点即为树尾端的NIL指针，或者说NULL结点。然百度百科以及网上一些其它博文直接说的叶结点，则易引起误会，因，此叶结点非子结点）

 

http://blog.csdn.net/v_july_v/article/details/6531399

2-3-4 树把数据存储在叫做元素的单独单元中。那么请问，到底什么是2-3-4树呢?顾名思义，就是有2个子女，3个子女，或4个子女的结点，这些含有2、3、或4个子女的结点就构成了我们的2-3-4树。所以，它们组合成结点，每个结点都是下列之一：
2-节点，就是说，它包含 1 个元素和 2 个儿子，
3-节点，就是说，它包含 2 个元素和 3 个儿子，
4-节点，就是说，它包含 3 个元素和 4 个儿子 。

 

http://blog.csdn.net/v_july_v/article/details/6530142

B 树又叫平衡多路查找树。一棵m阶的B 树 (注：切勿简单的认为一棵m阶的B树是m叉树，虽然存在四叉树，八叉树，KD树，及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树，但与B树完全不等同)的特性如下：

1. 树中每个结点最多含有m个孩子（m>=2）；
2. 除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
   
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
   
4. 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；（读者反馈@冷岳：这里有错，叶子节点只是没有孩子和指向孩子的指针，这些节点也存在，也有元素。@研究者July：其实，关键是把什么当做叶子结点，因为如红黑树中，每一个NULL指针即当做叶子结点，只是没画出来而已）。

5. 每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
          a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。 
          b)   Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。 
          c)   关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。如下图所示：

一棵R树满足如下的性质：

1.     除非它是根结点之外，所有叶子结点包含有m至M个记录索引（条目）。作为根结点的叶子结点所具有的记录个数可以少于m。通常，m=M/2。

2.     对于所有在叶子中存储的记录（条目），I是最小的可以在空间中完全覆盖这些记录所代表的点的矩形（注意：此处所说的“矩形”是可以扩展到高维空间的）。

3.     每一个非叶子结点拥有m至M个孩子结点，除非它是根结点。

4.     对于在非叶子结点上的每一个条目，i是最小的可以在空间上完全覆盖这些条目所代表的店的矩形（同性质2）。

5.     所有叶子结点都位于同一层，因此R树为平衡树。

叶子结点的结构

先来探究一下叶子结点的结构。叶子结点所保存的数据形式为：(I, tuple-identifier)。

      其中，tuple-identifier表示的是一个存放于数据库中的tuple，也就是一条记录，它是n维的。I是一个n维空间的矩形，并可以恰好框住这个叶子结点中所有记录代表的n维空间中的点。I=(I₀,I₁,…,I_n-1)。其结构如下图所示：

下图描述的就是在二维空间中的叶子结点所要存储的信息。

 

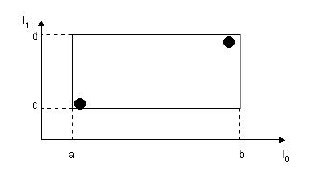
在这张图中，I所代表的就是图中的矩形，其范围是a<=I₀<=b，c<=I₁<=d。有两个tuple-identifier，在图中即表示为那两个点。这种形式完全可以推广到高维空间。大家简单想想三维空间中的样子就可以了。这样，叶子结点的结构就介绍完了。

 

非叶子结点

      非叶子结点的结构其实与叶子结点非常类似。想象一下B树就知道了，B树的叶子结点存放的是真实存在的数据，而非叶子结点存放的是这些数据的“边界”，或者说也算是一种索引（有疑问的读者可以回顾一下上述第一节中讲解B树的部分）。

      同样道理，R树的非叶子结点存放的数据结构为：(I, child-pointer)。

      其中，child-pointer是指向孩子结点的指针，I是覆盖所有孩子结点对应矩形的矩形。这边有点拗口，但我想不是很难懂？给张图：

 

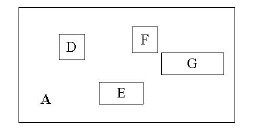
D,E,F,G为孩子结点所对应的矩形。A为能够覆盖这些矩形的更大的矩形。这个A就是这个非叶子结点所对应的矩形。这时候你应该悟到了吧？无论是叶子结点还是非叶子结点，它们都对应着一个矩形。树形结构上层的结点所对应的矩形能够完全覆盖它的孩子结点所对应的矩形。根结点也唯一对应一个矩形，而这个矩形是可以覆盖所有我们拥有的数据信息在空间中代表的点的。

我个人感觉这张图画的不那么精确，应该是矩形A要恰好覆盖D,E,F,G，而不应该再留出这么多没用的空间了。但为尊重原图的绘制者，特不作修改。

 

http://zh.wikipedia.org/wiki/%E5%93%88%E5%B8%8C%E8%A1%A8

散列表（Hash table，也叫哈希表），是根据关键字（Key value）而直接访问在内存存储位置的数据结构。也就是说，它通过把键值通过一个函数的计算，映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

一个通俗的例子是，为了查找电话簿中某人的号码，可以创建一个按照人名首字母顺序排列的表（即建立人名到首字母的一个函数关系），在首字母为W的表中查找“王”姓的电话号码，显然比直接查找就要快得多。这里使用人名作为关键字，“取首字母”是这个例子中散列函数的函数法则，存放首字母的表对应散列表。关键字和函数法则理论上可以任意确定。

 

 

http://dongxicheng.org/structure/heap/

http://zh.wikipedia.org/wiki/%E5%A0%86_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84)

http://www.cppblog.com/guogangj/archive/2009/10/29/99729.html

堆（英语：heap)亦被称为：优先队列（英语：priority queue），是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。在队列中，调度程序反复提取队列中第一个作业并运行，因而实际情况中某些时间较短的任务将等待很长时间才能结束，或者某些不短小，但具有重要性的作业，同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。

 

首先说说数据结构概念——堆（Heap），其实也没什么大不了，简单地说就是一种有序队列而已，普通的队列是先入先出，而二叉堆是：最小先出。

这不是很简单么？如果这个队列是用数组实现的话那用打擂台的方式从头到尾找一遍，把最小的拿出来不就行了？行啊，可是出队的操作是很频繁的，而每次都得打一遍擂台，那就低效了，打擂台的时间复杂度为Ο(n)，那如何不用从头到尾fetch一遍就出队呢？二叉堆能比较好地解决这个问题，不过之前先介绍一些概念。

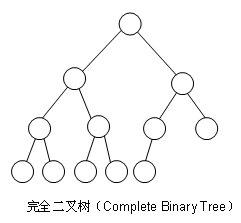
完全树（Complete Tree）：从下图中看出，在第n层深度被填满之前，不会开始填第n+1层深度，还有一定是从左往右填满。

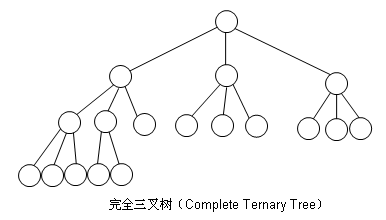
再来一棵完全三叉树：

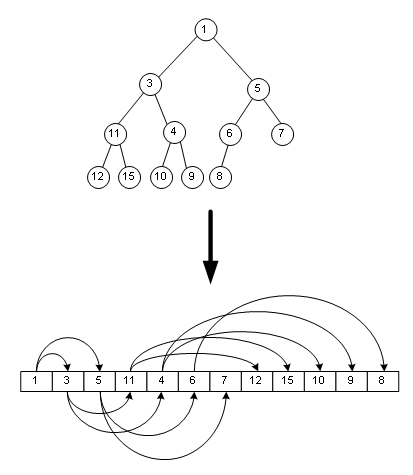
这样有什么好处呢？好处就是能方便地把指针省略掉，用一个简单的数组来表示一棵树，如图：

 

 

http://blog.chinaunix.net/uid-21813514-id-3866951.html

一、图的存储结构

1.1 邻接矩阵

    图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中的边或弧的信息。

    设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

    

    看一个实例，下图左就是一个无向图。

    

    从上面可以看出，无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足a_ij =
a_ji。即从矩阵的左上角到右下角的主对角线为轴，右上角的元和左下角相对应的元全都是相等的。

    从这个矩阵中，很容易知道图中的信息。

    （1）要判断任意两顶点是否有边无边就很容易了；

    （2）要知道某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行或（第i列）的元素之和；

    （3）求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点；

    而有向图讲究入度和出度，顶点vi的入度为1，正好是第i列各数之和。顶点vi的出度为2，即第i行的各数之和。

    若图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

    

    这里的w_ij表示(v_i,v_j)上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值，也就是一个不可能的极限值。下面左图就是一个有向网图，右图就是它的邻接矩阵。

    

那么邻接矩阵是如何实现图的创建的呢？代码如下。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129

#include <stdio.h> #include <stdlib.h> #include <curses.h>   typedef char VertexType;                 //顶点类型应由用户定义 typedef int EdgeType;                    //边上的权值类型应由用户定义   #define MAXVEX  100             //最大顶点数，应由用户定义 #define INFINITY    65535               //用65535来代表无穷大 #define DEBUG   typedef struct {      VertexType vexs[MAXVEX];             //顶点表      EdgeType   arc[MAXVEX][MAXVEX];          //邻接矩阵，可看作边      int numVertexes, numEdges;      //图中当前的顶点数和边数 }Graph;   //定位 int locates(Graph *g, char ch) {      int i = 0;      for (i = 0; i < g->numVertexes; i++)      {          if (g->vexs[i] == ch)          {              break ;          }      }      if (i >= g->numVertexes)      {          return -1;      }            return i; }   //建立一个无向网图的邻接矩阵表示 void CreateGraph(Graph *g) {      int i, j, k, w;      printf ( "输入顶点数和边数:\n" );      scanf ( "%d,%d" , &(g->numVertexes), &(g->numEdges));            #ifdef DEBUG      printf ( "%d %d\n" , g->numVertexes, g->numEdges);      #endif        for (i = 0; i < g->numVertexes; i++)      {          g->vexs[i] = getchar ();          while (g->vexs[i] == '\n' )          {              g->vexs[i] = getchar ();          }      }            #ifdef DEBUG      for (i = 0; i < g->numVertexes; i++)      {          printf ( "%c " , g->vexs[i]);      }      printf ( "\n" );      #endif          for (i = 0; i < g->numEdges; i++)      {          for (j = 0; j < g->numEdges; j++)          {              g->arc[i][j] = INFINITY; //邻接矩阵初始化          }      }      for (k = 0; k < g->numEdges; k++)      {          char p, q;          printf ( "输入边(vi,vj)上的下标i，下标j和权值:\n" );                    p = getchar ();          while (p == '\n' )          {              p = getchar ();          }          q = getchar ();          while (q == '\n' )          {              q = getchar ();          }          scanf ( "%d" , &w);                       int m = -1;          int n = -1;          m = locates(g, p);          n = locates(g, q);          if (n == -1 || m == -1)          {              fprintf (stderr, "there is no this vertex.\n" );              return ;          }          //getchar();          g->arc[m][n] = w;          g->arc[n][m] = g->arc[m][n];  //因为是无向图，矩阵对称      } }   //打印图 void printGraph(Graph g) {      int i, j;      for (i = 0; i < g.numVertexes; i++)      {          for (j = 0; j < g.numVertexes; j++)          {              printf ( "%d  " , g.arc[i][j]);          }          printf ( "\n" );      } }   int main( int argc, char **argv) {      Graph g;            //邻接矩阵创建图      CreateGraph(&g);      printGraph(g);      return 0; } </curses.h></stdlib.h></stdio.h>

      从代码中可以得到，n个顶点和e条边的无向网图的创建，时间复杂度为O(n + n ²  + e)，其中对邻接矩阵Grc的初始化耗费了O(n²)的时间。

1.2 邻接表

    邻接矩阵是不错的一种图存储结构，但是，对于边数相对顶点较少的图，这种结构存在对存储空间的极大浪费。因此，找到一种数组与链表相结合的存储方法称为邻接表。

    邻接表的处理方法是这样的：

    （1）图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过，数组可以较容易的读取顶点的信息，更加方便。

    （2）图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。

    例如，下图就是一个无向图的邻接表的结构。

    

    从图中可以看出，顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。

    对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域，存储权值信息即可。如下图所示。

    

    对于邻接表结构，图的建立代码如下。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155

/* 邻接表表示的图结构 */ #include <stdio.h> #include<stdlib.h>   #define DEBUG #define MAXVEX 1000         //最大顶点数 typedef char VertexType;        //顶点类型应由用户定义 typedef int EdgeType;           //边上的权值类型应由用户定义   typedef struct EdgeNode         //边表结点 {      int adjvex;         //邻接点域，存储该顶点对应的下标      EdgeType weigth;        //用于存储权值，对于非网图可以不需要      struct EdgeNode *next;      //链域，指向下一个邻接点 }EdgeNode;   typedef struct VertexNode       //顶点表结构 {      VertexType data;        //顶点域，存储顶点信息      EdgeNode *firstedge;        //边表头指针 }VertexNode, AdjList[MAXVEX];   typedef struct {      AdjList adjList;      int numVertexes, numEdges;  //图中当前顶点数和边数 }GraphList;   int Locate(GraphList *g, char ch) {      int i;      for (i = 0; i < MAXVEX; i++)      {          if (ch == g->adjList[i].data)          {              break ;          }      }      if (i >= MAXVEX)      {          fprintf (stderr, "there is no vertex.\n" );          return -1;      }      return i; }   //建立图的邻接表结构 void CreateGraph(GraphList *g) {      int i, j, k;      EdgeNode *e;      EdgeNode *f;      printf ( "输入顶点数和边数:\n" );      scanf ( "%d,%d" , &g->numVertexes, &g->numEdges);            #ifdef DEBUG      printf ( "%d,%d\n" , g->numVertexes, g->numEdges);      #endif            for (i = 0; i < g->numVertexes; i++)      {          printf ( "请输入顶点%d:\n" , i);          g->adjList[i].data = getchar ();          //输入顶点信息          g->adjList[i].firstedge = NULL;          //将边表置为空表          while (g->adjList[i].data == '\n' )          {              g->adjList[i].data = getchar ();          }      }      //建立边表      for (k = 0; k < g->numEdges; k++)      {          printf ( "输入边(vi,vj)上的顶点序号:\n" );          char p, q;          p = getchar ();          while (p == '\n' )          {              p = getchar ();          }          q = getchar ();          while (q == '\n' )          {              q = getchar ();          }          int m, n;          m = Locate(g, p);          n = Locate(g, q);          if (m == -1 || n == -1)          {              return ;          }          #ifdef DEBUG          printf ( "p = %c\n" , p);          printf ( "q = %c\n" , q);          printf ( "m = %d\n" , m);          printf ( "n = %d\n" , n);          #endif                //向内存申请空间，生成边表结点          e = (EdgeNode *) malloc ( sizeof (EdgeNode));          if (e == NULL)          {              fprintf (stderr, "malloc() error.\n" );              return ;          }          //邻接序号为j          e->adjvex = n;          //将e指针指向当前顶点指向的结构          e->next = g->adjList[m].firstedge;          //将当前顶点的指针指向e          g->adjList[m].firstedge = e;                    f = (EdgeNode *) malloc ( sizeof (EdgeNode));          if (f == NULL)          {              fprintf (stderr, "malloc() error.\n" );              return ;          }          f->adjvex = m;          f->next = g->adjList[n].firstedge;          g->adjList[n].firstedge = f;      } }     void printGraph(GraphList *g) {      int i = 0;      #ifdef DEBUG      printf ( "printGraph() start.\n" );      #endif            while (g->adjList[i].firstedge != NULL && i < MAXVEX)      {          printf ( "顶点:%c  " , g->adjList[i].data);          EdgeNode *e = NULL;          e = g->adjList[i].firstedge;          while (e != NULL)          {              printf ( "%d  " , e->adjvex);              e = e->next;          }          i++;          printf ( "\n" );      } }   int main( int argc, char **argv) {      GraphList g;      CreateGraph(&g);      printGraph(&g);      return 0; } </stdlib.h></stdio.h>

     对于无向图，一条边对应都是两个顶点，所以，在循环中，一次就针对i和j分布进行插入。

    本算法的时间复杂度，对于n个顶点e条边来说，很容易得出是O(n+e)。

1.3 十字链表

    对于有向图来说，邻接表是有缺陷的。关心了出度问题，想了解入度就必须要遍历整个图才知道，反之，逆邻接表解决了入度却不了解出度情况。下面介绍的这种有向图的存储方法：十字链表，就是把邻接表和逆邻接表结合起来的。

    重新定义顶点表结点结构，如下所示。

    

    其中firstin表示入边表头指针，指向该顶点的入边表中第一个结点，firstout表示出边表头指针，指向该顶点的出边表中的第一个结点。

    重新定义边表结构，如下所示。

    

    其中，tailvex是指弧起点在顶点表的下表，headvex是指弧终点在顶点表的下标，headlink是指入边表指针域，指向终点相同的下一条边，taillink是指边表指针域，指向起点相同的下一条边。如果是网，还可以增加一个weight域来存储权值。

    比如下图，顶点依然是存入一个一维数组，实线箭头指针的图示完全与邻接表相同。就以顶点v₀来说，firstout指向的是出边表中的第一个结点v₃。所以，v₀边表结点hearvex = 3，而tailvex其实就是当前顶点v₀的下标0，由于v₀只有一个出边顶点，所有headlink和taillink都是空的。

    

    重点需要解释虚线箭头的含义。它其实就是此图的逆邻接表的表示。对于v₀来说，它有两个顶点v₁和v₂的入边。因此的firstin指向顶点v1的边表结点中headvex为0的结点，如上图圆圈1。接着由入边结点的headlink指向下一个入边顶点v₂，如上图圆圈2。对于顶点v₁，它有一个入边顶点v₂，所以它的firstin指向顶点v₂的边表结点中headvex为1的结点，如上图圆圈3。

    十字链表的好处就是因为把邻接表和逆邻接表整合在一起，这样既容易找到以v为尾的弧，也容易找到以v为头的弧，因而比较容易求得顶点的出度和入度。

    而且除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的，因此，在有向图应用中，十字链表是非常好的数据结构模型。

    这里就介绍以上三种存储结构，除了第三种存储结构外，其他的两种存储结构比较简单。

二、图的遍历

    图的遍历和树的遍历类似，希望从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫图的遍历。

    对于图的遍历来说，如何避免因回路陷入死循环，就需要科学地设计遍历方案，通过有两种遍历次序方案：深度优先遍历和广度优先遍历。

2.1 深度优先遍历

    深度优先遍历，也有称为深度优先搜索，简称DFS。其实，就像是一棵树的前序遍历。

    它从图中某个结点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中的所有顶点都被访问到为止。

    我们用邻接矩阵的方式，则代码如下所示。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

#define MAXVEX  100     //最大顶点数 typedef int Boolean;             //Boolean 是布尔类型，其值是TRUE 或FALSE Boolean visited[MAXVEX];         //访问标志数组 #define TRUE 1 #define FALSE 0   //邻接矩阵的深度优先递归算法 void DFS(Graph g, int i) {      int j;      visited[i] = TRUE;      printf ( "%c " , g.vexs[i]);                            //打印顶点，也可以其他操作      for (j = 0; j < g.numVertexes; j++)      {          if (g.arc[i][j] == 1 && !visited[j])          {              DFS(g, j);                  //对为访问的邻接顶点递归调用          }      } }   //邻接矩阵的深度遍历操作 void DFSTraverse(Graph g) {      int i;      for (i = 0; i < g.numVertexes; i++)      {          visited[i] = FALSE;         //初始化所有顶点状态都是未访问过状态      }      for (i = 0; i < g.numVertexes; i++)      {          if (!visited[i])             //对未访问的顶点调用DFS，若是连通图，只会执行一次          {              DFS(g,i);          }      } }

    如果使用的是邻接表存储结构，其DFSTraverse函数的代码几乎是相同的，只是在递归函数中因为将数组换成了链表而有不同，代码如下。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

//邻接表的深度递归算法 void DFS(GraphList g, int i) {      EdgeNode *p;      visited[i] = TRUE;      printf ( "%c " , g->adjList[i].data);   //打印顶点，也可以其他操作      p = g->adjList[i].firstedge;      while (p)      {          if (!visited[p->adjvex])          {              DFS(g, p->adjvex);           //对访问的邻接顶点递归调用          }          p = p->next;      } }   //邻接表的深度遍历操作 void DFSTraverse(GraphList g) {      int i;      for (i = 0; i < g.numVertexes; i++)      {          visited[i] = FALSE;      }      for (i = 0; i < g.numVertexes; i++)      {          if (!visited[i])          {              DFS(g, i);          }      } }

      对比两个不同的存储结构的深度优先遍历算法，对于n个顶点e条边的图来说，邻接矩阵由于是二维数组，要查找某个顶点的邻接点需要访问矩阵中的所有元素，因为需要O(n ² )的时间。而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是O(n+e)。显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

2.2 广度优先遍历

    广度优先遍历，又称为广度优先搜索，简称BFS。图的广度优先遍历就类似于树的层序遍历了。

    邻接矩阵做存储结构时，广度优先搜索的代码如下。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

//邻接矩阵的广度遍历算法 void BFSTraverse(Graph g) {      int i, j;      Queue q;      for (i = 0; i < g.numVertexes; i++)      {          visited[i] = FALSE;      }      InitQueue(&q);      for (i = 0; i < g.numVertexes; i++) //对每个顶点做循环      {          if (!visited[i])               //若是未访问过          {              visited[i] = TRUE;              printf ( "%c " , g.vexs[i]); //打印结点，也可以其他操作              EnQueue(&q, i);           //将此结点入队列              while (!QueueEmpty(q))     //将队中元素出队列，赋值给              {                  int m;                  DeQueue(&q, &m);                         for (j = 0; j < g.numVertexes; j++)                  {                      //判断其他顶点若与当前顶点存在边且未访问过                      if (g.arc[m][j] == 1 && !visited[j])                      {                          visited[j] = TRUE;                          printf ( "%c " , g.vexs[j]);                          EnQueue(&q, j);                      }                  }              }          }      } } <span style= "line-height:2;font-family:'sans serif', tahoma, verdana, helvetica;" >  </span>

1

    对于邻接表的广度优先遍历，代码与邻接矩阵差异不大， 代码如下 。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

//邻接表的广度遍历算法 void BFSTraverse(GraphList g) {      int i;      EdgeNode *p;      Queue q;      for (i = 0; i < g.numVertexes; i++)      {          visited[i] = FALSE;      }      InitQueue(&q);      for (i = 0; i < g.numVertexes; i++)      {          if (!visited[i])          {              visited[i] = TRUE;              printf ( "%c " , g.adjList[i].data);   //打印顶点，也可以其他操作              EnQueue(&q, i);              while (!QueueEmpty(q))              {                  int m;                  DeQueue(&q, &m);                  p = g.adjList[m].firstedge;     找到当前顶点边表链表头指针                  while (p)                  {                      if (!visited[p->adjvex])                      {                          visited[p->adjvex] = TRUE;                          printf ( "%c " , g.adjList[p->adjvex].data);                          EnQueue(&q, p->adjvex);                      }                      p = p->next;                  }              }          }      } }<span style= "font-family:'sans serif', tahoma, verdana, helvetica;line-height:1.5;" >   </span>

1

      对比图的深度优先遍历与广度优先遍历算法，会发现，它们在时间复杂度上是一样的，不同之处仅仅在于对顶点的访问顺序不同。可见两者在全图遍历上是没有优劣之分的，只是不同的情况选择不同的算法。

    

        参考：《大话数据结构》