二分法及Python实现

Dfreedom.

已于 2023-09-14 09:23:37 修改

阅读量1w

点赞数 17

分类专栏：非线性方程求解文章标签：数值计算非线性方程求解二分法 python

于 2022-10-26 22:45:01 首次发布

本文链接：https://blog.csdn.net/dongke1991/article/details/127496768

版权

非线性方程求解专栏收录该内容

5 篇文章

订阅专栏

1 原理

连续函数零点定理：设 $f(x)\in [a,b]$ ，若 $f(a)f(b)<0$ ,方程 $f(x)=0$ 在(a,b)内至少有一个根；又若 $f'(x)$ 在(a,b)恒正或者恒负，则此根在(a,b)内唯一。

2 二分法求解

2.1 求解步骤

求解步骤分为两步：

① 确定方程的根区间；
② 若存在有根区间，采用二分法计算得到方程的解；若不存在有根区间，则报错：方程无实数解，或者返回方程的最小二乘解，需要评估最小二乘解是否满足精度需求。

2.1.1 确定有根区间

一般采用等步长扫描法来确定根区间。流程如下：

设扫描区间为[a,b]；
设定步长h>0，取x0=a，x1=x0+h；
若 $f(x0)f(x1)\leqslant 0$ ，则说明扫描成功，有根区间为[x0,x1]；否则令x0=x1，x1=x0+h继续扫描，直至成功；
如果在扫描的过程中出现x1>b则表明扫描失败，一般缩小步长h再次扫描，直到成功；
如果步长足够小时，仍然扫描失败，说明方程在区间[a,b]无实根。

2.1.2 二分法求根

在确定根区间以后，就可以采用二分法求得方程 $f(x)=0$ 在区间[x0,x1]的根。具体步骤如下：

输入有根区间[x0,x1]；
取x=(x0+x1)/2，计算 $f(x)$ 的值，如果f(x)=0，则方程的解为x，程序停止；
如果f(x0)f(x)<0，则令[x0,x1]=[x0,x]，如果f(x0)f(x)>0，则令[x0,x1]=[x,x1]。
重复上述三个步骤直至方程的解满足精度要求；
输出x的值，即为方程的数值解。

3 二分法的几何解释

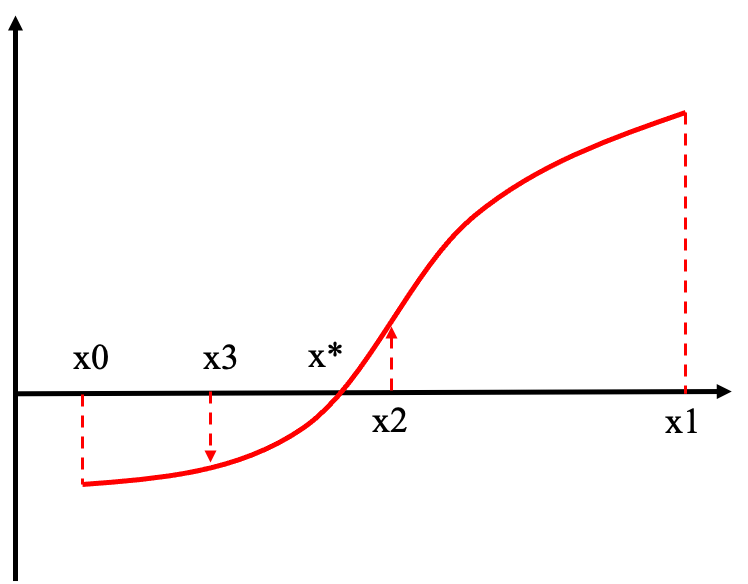
如图所示，x*为方程f(x)=0的真实解，迭代过程如下：

起始迭代区间为 $[x_0,x_1]$ ，计算对应的函数值 $f(x_0),f(x_1)$ ;
取 $x_2=(x_0+x_1)/2$ ，计算对应的函数值 $f(x_2)$ ;
根据函数值的符号更新迭代区间为 $[x_0,x_2]$ ；
取 $x_3=(x_0+x_2)/2$ ，计算对应的函数值 $f(x_3)$ ;
根据函数值的符号更新迭代区间为 $[x_3,x_2]$ ;
......
如此循环， $x_n$ 会无限逼近真实解 $x*$

4 案例&Python代码

求解方程 $f(x)=x^3-x-1=0$ 在区间[1,2]的根。

误差要求 $\varepsilon =0.001$

4.1 程序流程

4.2 Python代码

#二分法求根
import numpy as np
def f(x):
    y=x**3-x-1 #输入求根方程的表达式
    return y
def main():
    a = float(input("a="));b =float(input("b="))
    e = 0.001 #精度要求
    while f(a)*f(b)>0:
        print("请重新输入a、b的值")
        a = float(input("a="));b =float(input("b="))
    x0=(a+b)/2
    while np.abs(f(x0)-0)>e: #此处采用残差来判断
        if f(a)*f(x0)<0:
           a=a;b=x0
        else:
            a=x0;b=b
        x0=(a+b)/2
    print(x0)    #方程的解
    print(f(x0)) #验证解的正确性
if __name__ == '__main__':
   main()

运行结果：

a=1
b=2
1.32470703125
-4.659488331526518e-05

二分法及Python实现

1 原理

2 二分法求解

2.1 求解步骤

2.1.1 确定有根区间

2.1.2 二分法求根

3 二分法的几何解释

4 案例&Python代码

4.1 程序流程​​​​​​​

4.2 Python代码

4.1 程序流程