FFT快速傅里叶变换

FFT

我们从一个问题进行讨论$FFT$，我们有两个多项式$$\begin{gathered} A(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{n-1}{x}^{n-1}, \\ B(x)=b_0+b_{1}x+b_2{x}^2+\cdots +b_{m-1}{x}^{m-1} \end{gathered}$$我们现在要求$A(x)\cdot B(x)$。朴素算法是显而易见的，时间复杂度是$\Theta (nm)$暴力相乘即可，但这个时间复杂度我们是接受不了的。这时我们可以引入一个点值表示法。

前置知识

点值表示法

多项式通常有两种表示方法，一种是系数表示法即形如$P(x)={\sum }_{i=0}^{n-1}{a}_i{x}^i$的表示法，而点值表示法则是把$n$个互不相同的数$x$带入多项式$P(x)$中的的值作为$y$值确定$n$个点，我们可以证明互不重合的$n$个点可以唯一确定一个多项式。

单位根

对于${\omega }^n=1$的解傅里叶得出的结论是，对于${\omega }^n=1$这个方程的复数解为，在复平面上我们对单位圆从正实数轴开始$n$等分如图，这$n$个$n$等分点表示的复数即为原方程的复数解。

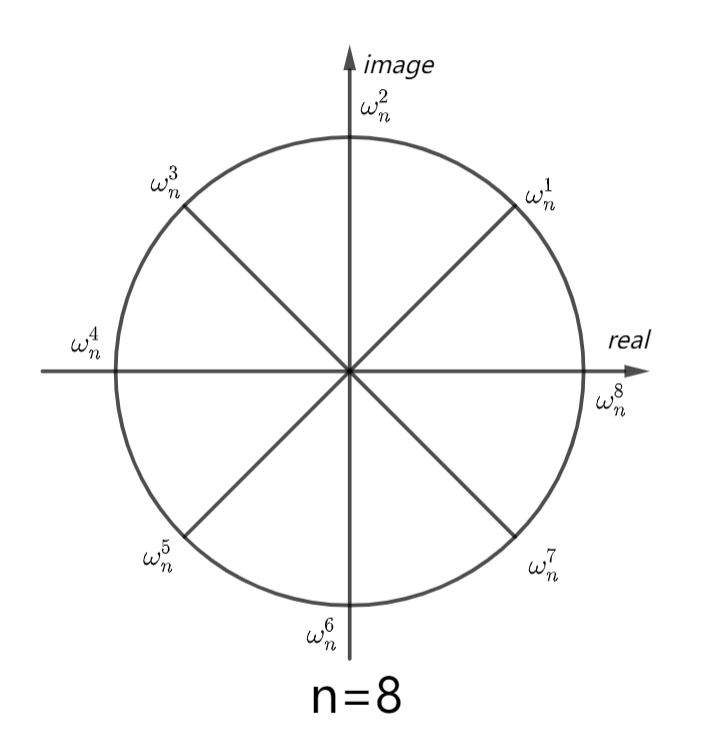
我们可以得到以下性质

• ${\omega }_n^k=\cos \frac{2k\pi }{n}+i\sin \frac{2k\pi }{n}$
• $\forall i\ne j$，$i,j<n$，有${\omega }_n^i\ne {\omega }_n^j$
• ${\omega }_{2n}^{2k}={\omega }_n^k$（折半引理）
• ${\omega }_n^k=-{\omega }_n^{k+\frac{n}{2}}$
• ${\omega }_n^0={\omega }_n^n$
• ${\omega }_n^i\cdot {\omega }_n^j={\omega }_n^{i+j}$

FFT推导

正变换

我们要把一个多项式转为点值表示法，朴素转是$\Theta (n^2)$，达不到我们的目的。这里我们要把$n$转为一个$2$的幂的数不够就补位系数补$0$，这样我们可以把多项式分为两个部分
$$\begin{array}{rl}A(x)& =a_0+a_{1}x+a_2{x}^2+\cdots +a_{n-1}{x}^{n-1}\\ & =(a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2})+(a_1+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1})\end{array}$$
令$A_1(x)=a_0+a_{2}x+\cdots +a_{n-2}{x}^{\frac{n}{2}-1}$，$A_2(x)=a_1+a_3{x}^2+\cdots +a_{n-1}{x}^{\frac{n}{2}-1}$

可得$A(x)=A_1(x^2)+x{A}_2(x^2)$

我们可以带入$n$个$n$次单位根
$$\begin{gathered} k\in [0,\frac{n}{2}-1],A({\omega }_n^k)=A_1({\omega }_n^{2k})+{\omega }_n^k{A}_2({\omega }_n^{2k})=A_1({\omega }_{\frac{n}{2}}^k)+{\omega }_n^k{A}_2({\omega }_{\frac{n}{2}}^k) \\ k\in [\frac{n}{2}-1,n-1],A({\omega }_n^{k+\frac{n}{2}})=A_1({\omega }_n^{2k+n})+{\omega }_n^{k+\frac{n}{2}}{A}_2({\omega }_n^{2k+n})=A_1({\omega }_{\frac{n}{2}}^k)-{\omega }_n^k{A}_2({\omega }_{\frac{n}{2}}^k) \end{gathered}$$
这样我们可以通过分治${\log }_{2}n$层，这样我们可以在$n{\log }_{2}n$的时间里求出$n$个单位根的多项式值，我们把两个多项式的每个单位根对应的多项式值算出来，把同一单位根的两个多项式的值相乘，便可以得到乘积多项式的点值表达式。但在一些数据优秀的$OJ$上我们并不能通过，所以我们需要一个蝴蝶变换来优化。

蝴蝶变换

我们会发现一个规律，一个项的最后拆分位置恰好为下标的二进制反过来，我们以$8$项的多项式为例，模拟拆分的过程：

位置编号（二进制）	$000$	$001$	$010$	$011$	$100$	$101$	$110$	$111$
初始序列	$x_0$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$
一次拆分后	$x_0$	$x_2$	$x_4$	$x_6$	$x_1$	$x_3$	$x_5$	$x_7$
两次拆分后	$x_0$	$x_4$	$x_2$	$x_6$	$x_1$	$x_5$	$x_3$	$x_7$
三次拆分后	$x_{0(000)}$	$x_{4(100)}$	$x_{2(010)}$	$x_{6(110)}$	$x_{1(001)}$	$x_{5(101)}$	$x_{3(011)}$	$x_{7(111)}$

我们就可以得到一个迭代版的$FFT$这样是可以通过所有$OJ$的洗礼的。

逆变换

正变换我们其实是求了这样一个东西
$$\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }_n^1& {\omega }_n^2& \cdots & {\omega }^{n-1}\\ 1& {\omega }_n^2& {\omega }_n^4& \cdots & {\omega }^{2n-2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }_{n-1}^{n-1}& {\omega }_{n-1}^{2n-2}& \cdots & {\omega }_{n-1}^{(n-1{)}^2}\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_{n-1}\end{array}\right]=\left[\begin{array}{c}{A}_0\\ A_1\\ A_2\\ ⋮\\ a_{n-1}\end{array}\right]$$
由于这个矩阵的元素非常特殊，它的逆矩阵也有特殊的性质，就是每一项取倒数再除以变换的长度就能得到它的逆矩阵。

我们可以得到
$$\frac{1}{{\omega }_k}={\omega }_k^{-1}=e^{-\frac{2\pi i}{k}}=\cos (\frac{2\pi }{k})+i\sin (-\frac{2\pi }{k})=\cos (\frac{2\pi }{k})-i\sin (\frac{2\pi }{k})$$
只需要我们在正变换的函数里面多传一个系数，表示正/逆变换，在计算的时候乘上系数即可。

code

const double Pi=acos(-1);
struct _cp{
    double re,im;
    inline _cp operator + (const _cp b)const
    {return (_cp){re+b.re,im+b.im};}
    inline _cp operator - (const _cp b)const
    {return (_cp){re-b.re,im-b.im};}
    inline _cp operator * (const _cp b)const
    {return (_cp){re*b.re-im*b.im,re*b.im+im*b.re};}
    inline _cp operator / (const _cp b)const{
        _cp x=(_cp){re,im};double q=b.re*b.re+b.im*b.im;
        _cp y=(_cp){b.re/q,b.im/q};
        return x*y;
    }
};//自己写的复数运算
int rev[5000005];
void FFT(_cp *a,int n,int inv)//inv为逆变换系数
{
    int bit=0;
    while((1<<bit)<n)bit++;
    for(int i=0;i<n;i++){
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
        if(i<rev[i])swap(a[i],a[rev[i]]);
    }
    for(int mid=1;mid<n;mid*=2){
    	_cp temp=(_cp){cos(Pi/mid),inv*sin(Pi/mid)};
        for(int i=0;i<n;i+=mid*2){
            _cp omega=(_cp){1,0};
            for(int j=0;j<mid;j++,omega=omega*temp){
                _cp x=a[i+j],y=omega*a[i+j+mid];
                a[i+j]=x+y,a[i+j+mid]=x-y;
            }
        }
    }
}