前置知识
(1)毕达哥拉斯定理: sin 2 α + cos 2 β = 1 \sin^2\alpha+\cos^2\beta=1 sin2α+cos2β=1
(2)诱导公式: sin ( 2 k π + α ) = sin α , cos ( 2 k π + α ) = cos α , ( k ∈ Z ) sin ( − α ) = − sin α , cos ( − α ) = cos α sin ( π + α ) = − sin α , cos ( π + α ) = − cos α \sin(2k\pi+\alpha)=\sin\alpha,\cos(2k\pi+\alpha)=\cos\alpha,(k\in Z)\\\sin(-\alpha)=-\sin\alpha,\cos(-\alpha)=\cos\alpha\\\sin(\pi+\alpha)=-\sin\alpha,\cos(\pi+\alpha)=-\cos\alpha sin(2kπ+α)=sinα,cos(2kπ+α)=cosα,(k∈Z)sin(−α)=−sinα,cos(−α)=cosαsin(π+α)=−sinα,cos(π+α)=−cosα
正弦定理
(1)定理:在 △ A B C \vartriangle ABC △ABC中 a , b , c a,b,c a,b,c分别为 A , B , C A,B,C A,B,C的对边,则 a sin A = b sin B = c sin C \frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C} sinAa=sinBb=sinCc
(2)证明:以
A
A
A为原点
A
B
AB
AB为
x
x
x轴正半轴,把
△
A
B
C
\vartriangle ABC
△ABC放在平面直角坐标系上,作
A
B
AB
AB边上的高CD,如图1
∴ A ( 0 , 0 ) , B ( c , 0 ) , C ( b cos A , b sin A ) , D ( b cos A , 0 ) \therefore A(0,0),B(c,0),C(b\cos A,b\sin A),D(b\cos A,0) ∴A(0,0),B(c,0),C(bcosA,bsinA),D(bcosA,0)
∴ C D = b sin A \therefore CD=b\sin A ∴CD=bsinA
∴ S △ A B C = 1 2 A D ⋅ C D = 1 2 b c sin A \therefore S\vartriangle ABC=\frac12AD\cdot CD=\frac12bc\sin A ∴S△ABC=21AD⋅CD=21bcsinA
同理 S △ A B C = 1 2 a b sin C = 1 2 a c sin B S\vartriangle ABC=\frac12ab\sin C=\frac12ac\sin B S△ABC=21absinC=21acsinB
∴ sin A a = sin B b = sin C c \therefore \frac{\sin A}a=\frac{\sin B}b=\frac{\sin C}c ∴asinA=bsinB=csinC
∴ a sin A = b sin B = c sin C \therefore\frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C} ∴sinAa=sinBb=sinCc
(2)扩充了的正弦定理: △ A B C \vartriangle ABC △ABC有外接圆半径为 R R R, a , b , c a,b,c a,b,c分别为 A , B , C A,B,C A,B,C的对边,则 a sin A = b sin B = c sin C = 2 R \frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}=2R sinAa=sinBb=sinCc=2R
(3)证明:过
B
B
B做外接圆的直径
B
D
BD
BD,连接
C
D
CD
CD,如图二
∴ ∠ A = ∠ D , sin A = sin D \therefore \angle A=\angle D,\sin A=\sin D ∴∠A=∠D,sinA=sinD
∵ B D \because BD ∵BD为直径
∴ ∠ D C B = 9 0 ∘ \therefore \angle DCB=90^{\circ} ∴∠DCB=90∘
∴ sin D = B C B D = a 2 R \therefore\sin D=\frac{BC}{BD}=\frac{a}{2R} ∴sinD=BDBC=2Ra
∴ a sin A = 2 R \therefore \frac a{\sin A}=2R ∴sinAa=2R
同理 a sin A = b sin B = c sin C = 2 R \frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}=2R sinAa=sinBb=sinCc=2R
余弦定理
(1)定理: a 2 = b 2 + c 2 − 2 b c cos A b 2 = a 2 + c 2 − 2 a c cos B c 2 = a 2 + b 2 − 2 a b cos C a^2=b^2+c^2-2bc\cos A\\b^2=a^2+c^2-2ac\cos B\\c^2=a^2+b^2-2ab\cos C a2=b2+c2−2bccosAb2=a2+c2−2accosBc2=a2+b2−2abcosC
(2)证明:如图一
∴ A ( 0 , 0 ) , B ( c , 0 ) , C ( b cos A , b sin A ) , D ( b cos A , 0 ) \therefore A(0,0),B(c,0),C(b\cos A,b\sin A),D(b\cos A,0) ∴A(0,0),B(c,0),C(bcosA,bsinA),D(bcosA,0)
∴ C D = b sin A \therefore CD=b\sin A ∴CD=bsinA
KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲\therefore a^2&…
同理 a 2 = b 2 + c 2 − 2 b c cos A b 2 = a 2 + c 2 − 2 a c cos B c 2 = a 2 + b 2 − 2 a b cos C a^2=b^2+c^2-2bc\cos A\\b^2=a^2+c^2-2ac\cos B\\c^2=a^2+b^2-2ab\cos C a2=b2+c2−2bccosAb2=a2+c2−2accosBc2=a2+b2−2abcosC
和角的余弦和正弦
(1)公式: sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β − sin α sin β \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta sin(α+β)=sinαcosβ+cosαsinβcos(α+β)=cosαcosβ−sinαsinβ
(2)证明:把角 α , β \alpha,\beta α,β,顶角放在原点,始边放在坐标系 x x x正半轴,终边分别放在 x x x轴两侧,如图三,把 B C BC BC绕原点旋转 β \beta β,如图四


∴ B ( cos α , sin α ) , C ( cos β , − sin β ) , B ′ ( cos α + β , sin α + β ) , C ′ ( 1 , 0 ) \therefore B(\cos\alpha,\sin\alpha),C(\cos\beta,-\sin\beta),B'(\cos\ \alpha+\beta,\sin\ \alpha+\beta),C'(1,0) ∴B(cosα,sinα),C(cosβ,−sinβ),B′(cos α+β,sin α+β),C′(1,0)
∴ B C 2 = ( cos α − cos β ) 2 + ( sin α + sin β ) 2 = 2 + 2 ( sin α sin β − cos α cos β ) B ′ C ′ 2 = [ cos ( α + β ) − 1 ] 2 + sin 2 ( α + β ) = 2 − 2 cos ( α + β ) \therefore BC^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha+\sin\beta)^2=2+2(\sin\alpha\sin\beta-\cos\alpha\cos\beta)\\B'C'^2=[\cos(\alpha+\beta)-1]^2+\sin^2(\alpha+\beta)=2-2\cos(\alpha+\beta) ∴BC2=(cosα−cosβ)2+(sinα+sinβ)2=2+2(sinαsinβ−cosαcosβ)B′C′2=[cos(α+β)−1]2+sin2(α+β)=2−2cos(α+β)
∵ B C = B ′ C ′ \because BC=B'C' ∵BC=B′C′
∴ B C 2 = B ′ C ′ 2 \therefore BC^2=B'C'^2 ∴BC2=B′C′2
∴ cos ( α + β ) = cos α cos β − sin α sin β \therefore \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta ∴cos(α+β)=cosαcosβ−sinαsinβ
∴ sin ( α + β ) = cos ( π − α − β ) = cos ( π − α ) cos β + sin ( π − α ) sin β = sin α cos β + sin β cos α \therefore \sin(\alpha+\beta)=\cos(\pi-\alpha-\beta)=\cos(\pi-\alpha)\cos\beta+\sin(\pi-\alpha)\sin\beta=\sin\alpha\cos\beta+\sin\beta\cos\alpha ∴sin(α+β)=cos(π−α−β)=cos(π−α)cosβ+sin(π−α)sinβ=sinαcosβ+sinβcosα
*(3)托勒密定理与和角定理互证:
有 A , B , C , D A,B,C,D A,B,C,D四点共圆,有四边形 A B C D ABCD ABCD,则 A B ⋅ C D + B C ⋅ A D = A C ⋅ B D ⇔ sin ( α + β ) = sin α cos β + cos α sin β AB\cdot CD+BC\cdot AD=AC\cdot BD\Leftrightarrow\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta AB⋅CD+BC⋅AD=AC⋅BD⇔sin(α+β)=sinαcosβ+cosαsinβ
1、 A B ⋅ C D + B C ⋅ A D = A C ⋅ B D ⇒ sin ( α + β ) = sin α cos β + cos α sin β AB\cdot CD+BC\cdot AD=AC\cdot BD\Rightarrow\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta AB⋅CD+BC⋅AD=AC⋅BD⇒sin(α+β)=sinαcosβ+cosαsinβ
做
A
,
B
,
C
,
D
A,B,C,D
A,B,C,D四点共圆,有直径
A
C
AC
AC,如图五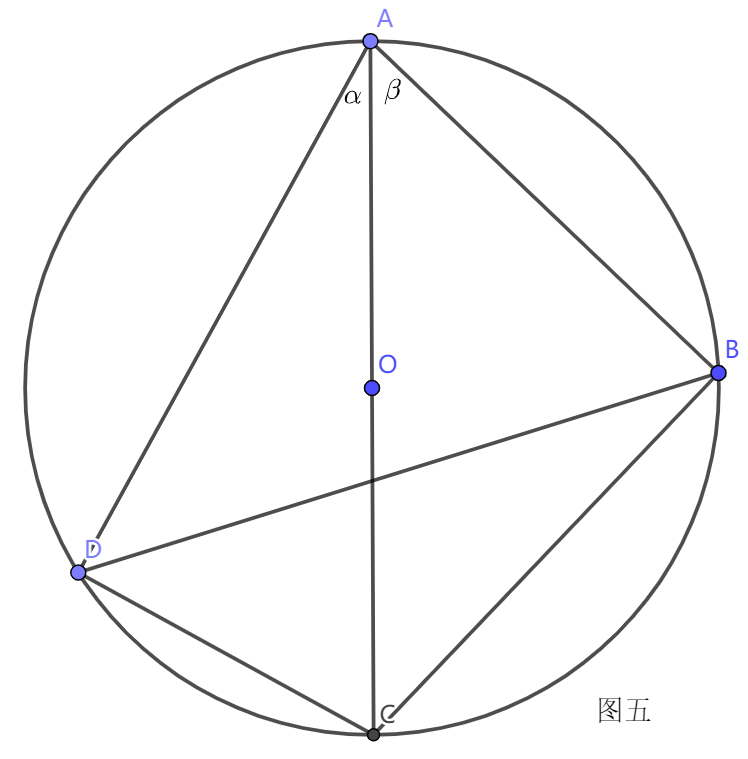
∵ A C 为 圆 O 的 直 径 \because AC为圆O的直径 ∵AC为圆O的直径
∴ ∠ A D C = ∠ A B C = 9 0 ∘ \therefore \angle ADC=\angle ABC=90^{\circ} ∴∠ADC=∠ABC=90∘
∴ sin α = D C A C , cos α = A D A C , sin β = B C A C , cos β = A B A C \therefore \sin\alpha=\frac{DC}{AC},\cos\alpha=\frac{AD}{AC},\sin\beta=\frac{BC}{AC},\cos\beta=\frac{AB}{AC} ∴sinα=ACDC,cosα=ACAD,sinβ=ACBC,cosβ=ACAB
∴ sin α cos β + c o s α sin β = A D ⋅ B C + D C ⋅ A B A C 2 \therefore\sin\alpha\cos\beta+cos\alpha\sin\beta=\frac{AD\cdot BC+DC\cdot AB}{AC^2} ∴sinαcosβ+cosαsinβ=AC2AD⋅BC+DC⋅AB
∵ A B ⋅ C D + B C ⋅ A D = A C ⋅ B D \because AB\cdot CD+BC\cdot AD=AC\cdot BD ∵AB⋅CD+BC⋅AD=AC⋅BD
∴ sin α cos β + c o s α sin β = A C ⋅ B D A C 2 = B D A C \therefore\sin\alpha\cos\beta+cos\alpha\sin\beta=\frac{AC\cdot BD}{AC^2}=\frac{BD}{AC} ∴sinαcosβ+cosαsinβ=AC2AC⋅BD=ACBD
∵ B D sin ( α + β ) = 2 R = A C \because\frac{BD}{\sin(\alpha+\beta)}=2R=AC ∵sin(α+β)BD=2R=AC
∴ ∴ sin α cos β + c o s α sin β = sin ( α + β ) \therefore\therefore\sin\alpha\cos\beta+cos\alpha\sin\beta=\sin(\alpha+\beta) ∴∴sinαcosβ+cosαsinβ=sin(α+β)
2、 A B ⋅ C D + B C ⋅ A D = A C ⋅ B D ⇐ sin ( α + β ) = sin α cos β + cos α sin β AB\cdot CD+BC\cdot AD=AC\cdot BD\Leftarrow\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta AB⋅CD+BC⋅AD=AC⋅BD⇐sin(α+β)=sinαcosβ+cosαsinβ
有
A
,
B
,
C
,
D
A,B,C,D
A,B,C,D四点共圆,如图六
由正弦定理得
A
B
⋅
C
D
+
B
C
⋅
A
D
=
sin
β
⋅
2
R
⋅
sin
α
⋅
2
R
+
sin
θ
⋅
2
R
⋅
sin
γ
⋅
2
R
A
C
⋅
B
D
=
sin
(
β
+
θ
)
sin
(
β
+
γ
)
AB\cdot CD+BC\cdot AD=\sin\beta\cdot2R\cdot\sin\alpha\cdot2R+\sin\theta\cdot2R\cdot\sin\gamma\cdot2R\\AC\cdot BD=\sin(\beta+\theta)\sin(\beta+\gamma)
AB⋅CD+BC⋅AD=sinβ⋅2R⋅sinα⋅2R+sinθ⋅2R⋅sinγ⋅2RAC⋅BD=sin(β+θ)sin(β+γ)
sin
β
sin
α
+
sin
θ
sin
γ
=
sin
β
sin
(
π
−
β
−
θ
−
γ
)
+
sin
θ
sin
γ
(
诱
导
公
式
)
=
sin
β
sin
(
β
+
θ
+
γ
)
+
sin
θ
sin
γ
=
sin
β
sin
(
β
+
θ
)
cos
γ
+
sin
β
cos
(
β
+
θ
)
sin
γ
+
sin
θ
sin
γ
=
sin
2
β
cos
γ
cos
θ
+
sin
β
cos
β
cos
γ
sin
θ
+
sin
β
sin
γ
cos
β
cos
θ
−
sin
2
β
sin
γ
sin
θ
+
sin
θ
sin
γ
(
毕
达
哥
拉
斯
定
理
)
=
sin
θ
sin
γ
cos
2
β
+
sin
2
β
cos
γ
cos
θ
+
sin
β
cos
β
cos
γ
sin
θ
+
sin
β
sin
γ
cos
β
cos
θ
(
因
式
分
解
)
=
(
cos
β
sin
θ
+
sin
β
cos
θ
)
(
cos
β
sin
γ
+
sin
β
cos
γ
)
(
和
角
的
正
弦
公
式
)
=
sin
(
β
+
θ
)
sin
(
β
+
γ
)
\sin\beta\sin\alpha+\sin\theta\sin\gamma\\=\sin\beta\sin(\pi-\beta-\theta-\gamma)+\sin\theta\sin\gamma(诱导公式)\\=\sin\beta\sin(\beta+\theta+\gamma)+\sin\theta\sin\gamma\\ =\sin\beta\sin(\beta+\theta)\cos\gamma+\sin\beta\cos(\beta+\theta)\sin\gamma+\sin\theta\sin\gamma\\=\sin^2\beta\cos\gamma\cos\theta+\sin\beta\cos\beta\cos\gamma\sin\theta+\sin\beta\sin\gamma\cos\beta\cos\theta-\sin^2\beta\sin\gamma\sin\theta+\sin\theta\sin\gamma(毕达哥拉斯定理)\\=\sin\theta\sin\gamma\cos^2\beta+\sin^2\beta\cos\gamma\cos\theta+\sin\beta\cos\beta\cos\gamma\sin\theta+\sin\beta\sin\gamma\cos\beta\cos\theta(因式分解)\\=(\cos\beta\sin\theta+\sin\beta\cos\theta)(\cos\beta\sin\gamma+\sin\beta\cos\gamma)(和角的正弦公式)\\ =\sin(\beta+\theta)\sin(\beta+\gamma)
sinβsinα+sinθsinγ=sinβsin(π−β−θ−γ)+sinθsinγ(诱导公式)=sinβsin(β+θ+γ)+sinθsinγ=sinβsin(β+θ)cosγ+sinβcos(β+θ)sinγ+sinθsinγ=sin2βcosγcosθ+sinβcosβcosγsinθ+sinβsinγcosβcosθ−sin2βsinγsinθ+sinθsinγ(毕达哥拉斯定理)=sinθsinγcos2β+sin2βcosγcosθ+sinβcosβcosγsinθ+sinβsinγcosβcosθ(因式分解)=(cosβsinθ+sinβcosθ)(cosβsinγ+sinβcosγ)(和角的正弦公式)=sin(β+θ)sin(β+γ)
∴
A
B
⋅
C
D
+
B
C
⋅
A
D
=
A
C
⋅
B
D
\therefore AB\cdot CD+BC\cdot AD=AC\cdot BD
∴AB⋅CD+BC⋅AD=AC⋅BD
和差化积与积化和差
(1)积化和差:
sin
α
cos
β
=
1
2
[
sin
(
α
+
β
)
+
sin
(
α
−
β
)
]
(
两
角
和
的
正
弦
公
式
相
加
可
得
)
cos
α
sin
β
=
1
2
[
sin
(
α
+
β
)
−
sin
(
α
−
β
)
]
(
两
角
和
的
正
弦
公
式
相
减
可
得
)
sin
α
sin
β
=
1
2
[
cos
(
α
+
β
)
+
cos
(
α
−
β
)
]
(
两
角
和
的
余
弦
公
式
相
加
可
得
)
sin
α
sin
β
=
1
2
[
cos
(
α
+
β
)
−
cos
(
α
−
β
)
]
(
两
角
和
的
余
弦
公
式
相
减
可
得
)
\sin\alpha\cos\beta=\frac12[\sin(\alpha+\beta)+\sin(\alpha-\beta)](两角和的正弦公式相加可得)\\ \cos\alpha\sin\beta=\frac12[\sin(\alpha+\beta)-\sin(\alpha-\beta)](两角和的正弦公式相减可得)\\ \sin\alpha\sin\beta=\frac12[\cos(\alpha+\beta)+\cos(\alpha-\beta)](两角和的余弦公式相加可得)\\ \sin\alpha\sin\beta=\frac12[\cos(\alpha+\beta)-\cos(\alpha-\beta)](两角和的余弦公式相减可得)
sinαcosβ=21[sin(α+β)+sin(α−β)](两角和的正弦公式相加可得)cosαsinβ=21[sin(α+β)−sin(α−β)](两角和的正弦公式相减可得)sinαsinβ=21[cos(α+β)+cos(α−β)](两角和的余弦公式相加可得)sinαsinβ=21[cos(α+β)−cos(α−β)](两角和的余弦公式相减可得)
(2)和差化积
令
α
+
β
=
A
,
α
−
β
=
B
,
有
α
=
A
+
B
2
,
β
=
A
−
B
2
,
代
入
积
化
和
差
得
sin
A
+
sin
B
=
2
sin
A
+
B
2
cos
A
−
B
2
sin
A
−
sin
B
=
2
cos
A
+
B
2
sin
A
−
B
2
cos
A
+
cos
B
=
2
cos
A
+
B
2
cos
A
−
B
2
cos
A
−
cos
B
=
−
2
sin
A
+
B
2
sin
A
−
B
2
令\alpha+\beta=A,\alpha-\beta=B,有\alpha=\frac{A+B}2,\beta=\frac{A-B}2,代入积化和差得\\ \sin A+\sin B=2\sin\frac{A+B}2\cos\frac{A-B}2\\ \sin A-\sin B=2\cos\frac{A+B}2\sin\frac{A-B}2\\ \cos A+\cos B=2\cos\frac{A+B}2\cos\frac{A-B}2\\ \cos A-\cos B=-2\sin\frac{A+B}2\sin\frac{A-B}2\\
令α+β=A,α−β=B,有α=2A+B,β=2A−B,代入积化和差得sinA+sinB=2sin2A+Bcos2A−BsinA−sinB=2cos2A+Bsin2A−BcosA+cosB=2cos2A+Bcos2A−BcosA−cosB=−2sin2A+Bsin2A−B
























 521
521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








