1.题目链接:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
3. 解法(暴搜 -> 记忆化搜索 -> 动态规划):
算法思路:
暴搜:
a. 递归含义:给 dfs 一个使命,给他一个下标,返回从 [0, 0] 位置走到 [i, j] 位置一共有多少种方法;
b. 函数体:只要知道到达上面位置的方法数以及到达左边位置的方法数,然后累加起来即可;
c. 递归出口:当下标越界的时候返回 0 ;当位于起点的时候,返回 1 。
记忆化搜索:
a. 加上一个备忘录;
b. 每次进入递归的时候,去备忘录里面看看;c. 每次返回的时候,将结果加入到备忘录里面。
动态规划:
a. 递归含义 -> 状态表示;
b. 函数体 -> 状态转移方程;
c. 递归出口 -> 初始化。
Java算法代码:
class Solution {
public int uniquePaths(int m, int n) {
//动态规划
int[][] dp = new int[m+1][n+1];
dp[1][1] = 1;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++){
if(i == 1 && j ==1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
return dp[m][n];
记忆化搜索
int [][] memo = new int[m+1][n+1];
return dfs(m,n,memo);
}
public int dfs(int i, int j, int[][] memo){
if(memo[i][j] != 0) return memo[i][j];
if(i == 0 || j == 0) return 0;
if(i == 1 && j == 1){
memo[i][j] = 1;
return 1;
}
memo[i][j] = dfs(i - 1, j, memo) +dfs(i, j - 1, memo);
return memo[i][j];
}
}运行结果:

递归展开:
这里是从动态规划进行展开的箭头图和记忆化搜索的箭头图。
如果能看懂这个流程,说明,读者就已经明白这个题目了。
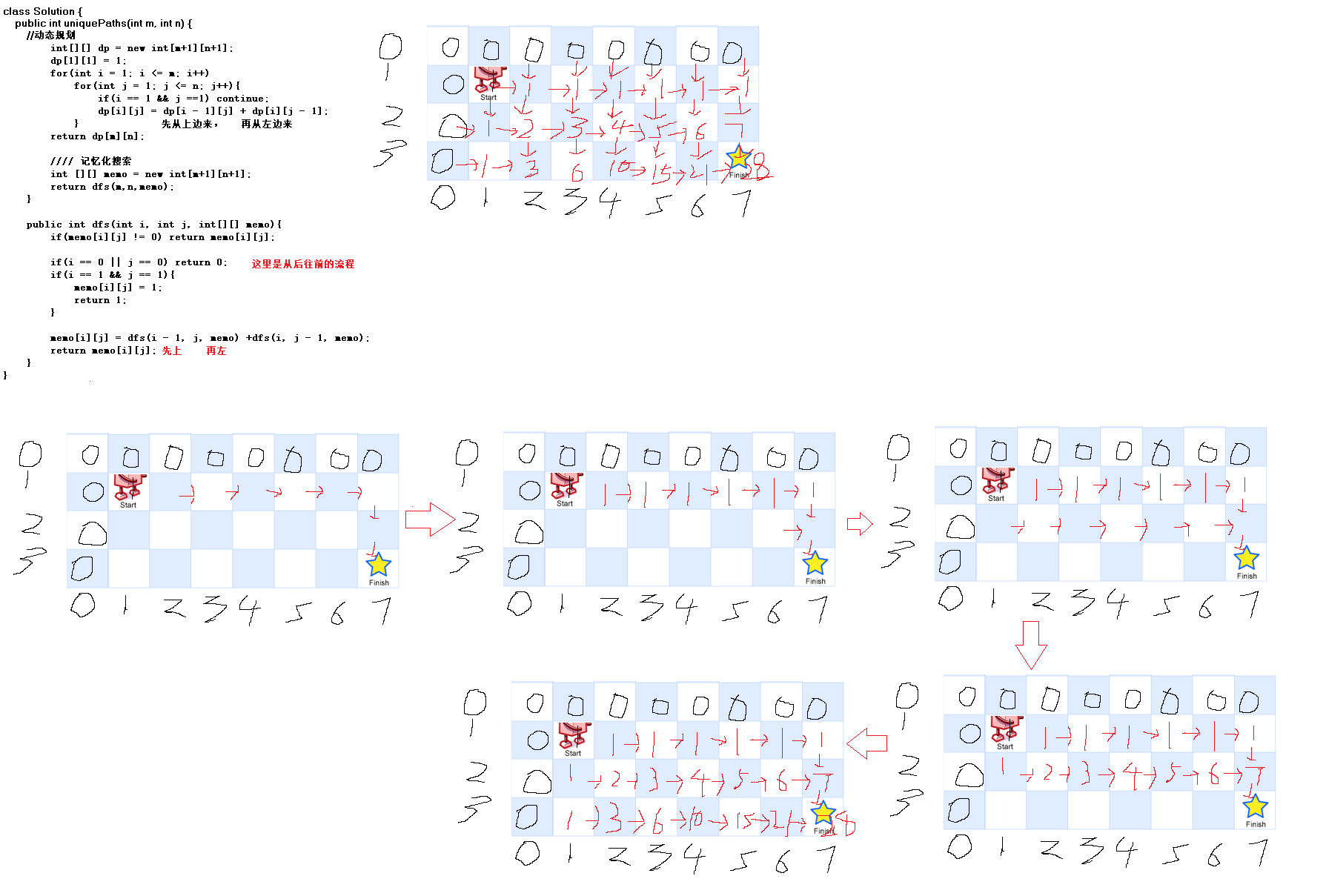
逻辑展开:明白整个流程之后,就可以自己直接画出来箭头图。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








