GAN-文献阅读笔记

论文简介

论文提出一个新的框架，通过对抗过程评估生成模型。论文中同时训练两个网络：一个生成模型G用来捕获数据分布，一个有识别力的模型D用来评估来自训练数据样本的可能性。G的训练过程是去最大化D犯错的可能性。这个框架对应一个minimax的双人游戏。在G和D的任意函数空间，存在一个独特的解，G回复训练数据分布，D等于1/2.在G和D通过多层感知机定义，整个系统可以通过反向传播训练。在训练或者生成样本时，没有必要有任何马尔科夫链或者展开近似推理网络。实验通过对生成样本进行定性和定量评估证明了框架的潜力。

引言

深度生成模型由于难以逼近在最大似然估计和相关策略中出现的许多难以解决的概率及算法，以及在生成上下文中难以利用分断线性单元的优点。我们提出一种新的生成模型评估方式，避免了这些困难。

本文提出的对抗网络框架，生成模型与另一个判别模型对抗，判别模型会学习区分一个样本是来自模型分布还是数据集分布。生成模型可以看成是伪钞制造者，试图生产假币而不被检测到，而识别模型就像警察，试图检测伪钞。这种互相竞争会驱使双方改进他们的方法直到伪钞和真币区分不开来。

这种框架可以为许多种模型和优化算法生成特定训练算法。本文中，作者探究了特殊的情况：生成模型使用多层感知机通过随机噪音生成样本，识别模型也是一个多层感知机。作者把这种特殊情况称为对抗网络。在这种情况下，可以使用非常成功的反向传播和dropout算法来训练两个模型，并且生成模型的样本只使用前向传播。不需要近似推理或者马尔科夫链。

生成网络

当模型都是多层感知机时，生成建模框架可以直接应用。为了学习生成器在数据$x$ 的分布$p_g$，我们定义了一个关于输入噪音变量的先验$p_z(z)$ ，然后将到数据空间的映射表示为$G(z;{\theta }_g)$ ，其中$G$ 是一个可微函数，有一个参数为${\theta }_g$ 的多层感知机表示。我们还定义了第二个输出单个标量的多层感知器$D(x;{\theta }_d)$ 。$D(x)$ 表示x来自数据集而不是$p_g$ 的概率。我们训练$D$ 以最大化为训练样本和来自$G$ 的样本分配正确标签的概率。我们同时训练$G$ 去最小化$\log (1-D(G(z)));$

换句话说，$D$ 和$G$ 扮演下列函数$V(G,D)$ 的双人最小最大化游戏：

$\underset{G}{\min }\underset{D}{\max }V(D,G)={\mathbb{E}}_{x\sim p_{data}(x)}[\log D(x)]+{\mathbb{E}}_{z\sim p_z(z)}[\log (1-D(G(z)))]$

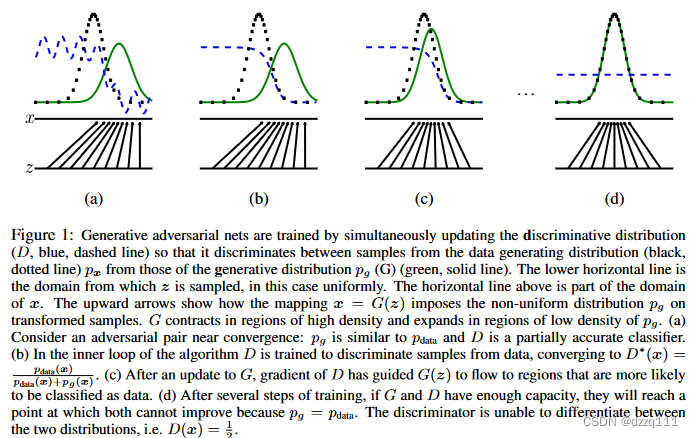
图一展示了生成对抗网络的训练过程，其中识别器分布D是蓝色虚线，生成器G的分布是绿色实线，记为$p_g(x)$ ;数据样本是黑色虚线,记为$p_{data}(x)$ 。生成对抗网络通过同时更新识别器分布来训练，使得它可以识别数据生成分布的样本$p_x$ 和生成的分布$p_g$ 。较低的水平线是噪音样本z被采样的区域，在这种情况下是均匀的。上方的水平线是数据x的区域。向上的箭头显示了映射$x=G(z)$ 如何将非均匀分布$p_g$ 施加在变换后的样本上。$G$ 在$p_g$ 的高密度区域收缩，在其低密度区域扩张。

1. 考虑一个在收敛点附近的对抗对：$p_g$ 与$p_{data}$是相似的，D是一个部分准确的分类器。

2. 在算法的内层循环中，D被训练识别来自数据集的样本，收敛于$D^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$ 。

3. 更新G之后，D的梯度引导$G(z)$ 流向其更可能被分类为数据集的区域。

4. 经过几轮训练后，如果G和D有足够的能力，他们将会达到一个两者都不能再进步的点，此时$p_g=p_{data}$ 。识别器不能够区分两个分布的不同，也就是说$D(x)=\frac{1}{2}$ 。

理论计算

生成器隐含地定义了一个概率分布$p_g$ ，当$z\sim p_z$ 时它就是得到的样本$G(z)$ 的分布。因此，如果给定足够足够的容量和训练时间，算法1可以收敛到一个好的$p_g$ 的估计量。本节的结果是在非参数设定下完成的，例如，我们通过研究概率密度函数空间中的收敛性来表示具有无限容量的模型。

算法的全局优化目标就是$p_g=p_{data}$ ，并且对方程(1)进行了优化，从而获得所需的结果。

算法一先是从噪音先验概率$p_g(z)$ 中采样m个噪音样本的最小批，也从数据生成分布$p_{data}(x)$ 采样m个样本的最小批数据，然后对识别器使用随机梯度上升进行更新，梯度计算公式如下：

${\nabla }_{{\theta }_d}\frac{1}{m}\sum _{i=1}^m[\log D(x^{(i)})+\log (1-D(G(z^{(i)})))]$

这个过程会迭代k次。

然后从噪音分布先验概率样本中采样m个最小批样本，再通过随机梯度下降更新生成器：

${\nabla }_{{\theta }_g}\frac{1}{m}\sum _{i=1}^m\log (1-D(G(z^{(i)})))$

上述过程是训练的一个迭代，根据超参设置会迭代多次。

算法中基于梯度的更新可以使用任何标准的基于梯度的学习规则。在实验中使用的是动量（momentum）。

全局最优化

首先考虑对任意给定的生成器G的最优化判别器D。

命题1：对于固定的G，最优判别器D：
$$D_G^{\ast }(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$$
证明：给定任意生成器G，判别器D的训练准则是最大化$V(G,D)$ 的数量：
$$\begin{gathered} V(G,D)={\int }_x{p}_{data}(x)log(D(x))dx+{\int }_z{p}_z(z)log(1-D(g(z)))dz \\ ={\int }_x{p}_{data}(x)log(D(x))+p_g(x)log(1-D(x)dx \end{gathered}$$
对于任意的 ( a , b ) ∈ R 2 \ { 0 , 0 } (a,b) \in \mathbb{R}^2 \backslash \{0,0\} (a,b)∈R2\{0,0} ,函数$y->a\log (y)+b\log (1-y)在$$[0,1]$区间的最大值在$\frac{a}{a+b}$ 。判别器不需要在$Supp(p_{data})\cup Supp(p_g)$ 之外定义，从而完成证明。

注意，D的训练目标可以理解为最大化估计条件概率$P(Y=y|x)$的对数似然，其中$Y$ 表示$x$ 是来自$p_{data}(y=1)$ 还是来自$p_g$ (当$y=0$ 时)。方程1中的最小最大化游戏现在可以重新表述为：
$$\begin{gathered} C(G)=\underset{D}{\max }V(G,D) \\ ={\mathbb{E}}_{x\sim p_{data}}[\log D_G^{\ast }(x)]+{\mathbb{E}}_{z\sim p_z}[\log (1-D_G^{\ast }(G(z)))] \\ ={\mathbb{E}}_{x\sim p_{data}}[\log D_G^{\ast }(x)]+{\mathbb{E}}_{x\sim p_g}[\log (1-D_G^{\ast }(x))] \\ ={\mathbb{E}}_{x\sim p_{data}}\left[\log \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}\right]+{\mathbb{E}}_{x\sim p_g}\left[\log \frac{p_g(x)}{p_{data}(x)+p_g(x)}\right] \end{gathered}$$
定理1。当且仅当$p_g=p_{data}$ 时，虚拟训练准则$C(G)$ 达到全局最小值.此时，$C(G)$ 达到$-\log 4$ 。

证明。对于$p_g=p_{data}，D^{\ast }G(x)=\frac{1}{2}$ ，(考虑等式。2 )。因此，通过考察Eq . 4在$D_G^{\ast }(x)=\frac{1}{2}$ 处，我们发现$C(G)=\log \frac{1}{2}+\log \frac{1}{2}=-\log 4$ 。要看这是$C(G)$ 的最佳可能值，只达到了对于$p_g=p_{data}$ ，观察到
$${\mathbb{E}}_{x\sim p_{data}}[-\log 2]+{\mathbb{E}}_{x\sim p_g}[-\log 2]=-\log 4$$
通过从$C(G)=V(D_G^{\ast },G)$ 减去这个表达式，我们得到：
$$C(G)=-\log (4)+KL\left(p_{data}\Vert \frac{p_{data}+p_g}{2}\right)+KL\left(p_g\Vert \frac{p_{data}+p_g}{2}\right)$$
其中KL为Kullback-Leibler库尔贝克-莱布勒散度。我们在前面的表达式中认识到了模型的分布和数据生成过程之间的Jensen - Shannon散度:
$$C(G)=-\log (4)+2\cdot JSD(p_{data}\Vert p_g)$$
由于两个分布之间的Jensen - Shannon散度总是非负的，并且只有当它们相等时才为零，因此我们证明了$C^{\ast }=-\log (4)$ 是$C(G)$ 的全局最小值，并且唯一的解是$p_g=p_{data}$ ，即生成模型完美地复制了数据生成过程。

算法1的收敛

命题2。如果G和D有足够的容量，并且在算法1的每个步骤中，判别器被允许在给定G的情况下达到最优，并且$p_g$ 被更新以改进判据
$${\mathbb{E}}_{x\sim p_{data}}[\log D_G^{\ast }(x)]+{\mathbb{E}}_{x\sim p_g}[\log (1-D_G^{\ast }(x))]$$
之后$p_{g}convergesto{p}_{data}$

证明。考虑$V(G,D)=U(p_g,D)$ 作为$p_g$ 的函数，如上面的条件所示。注意到$U(p_g,D)$ 是以$p_g$ 为单位的凸函数。凸函数上确界的次导数包括函数在达到最大值点处的导数.换句话说，如果$f(x)=su{p}_{\alpha \in A}{f}_{\alpha }(x)$且对于每个$\alpha$ ，$f_{\alpha }(x)$在$x$ 上是凸的，那么$\partial f_{\beta }(x)\in \partial f$ 如果$\beta =arg{\sup }_{\alpha \in A}{f}_{\alpha }(x)$ 。这相当于在给定相应的$G$ 的情况下，计算$p_g$ 在最优$D$ 处的梯度下降更新。${\sup }_{D}U(p_g,D)$ 在$p_g$ 上是凸的，存在Thm 1中证明的唯一全局最优解，因此当$p_g$ 的更新充分小时，$p_g$ 收敛到$p_x$ ，证明完毕。

在实际中，对抗网络通过函数$G(z;{\theta }_g)$ 表示有限的$p_g$ 分布族，我们优化${\theta }_g$ 而不是$p_g$ 本身。使用多层感知器来定义$G$ 在参数空间中引入了多个临界点。然而，多层感知器在实践中的优异表现表明，尽管它们缺乏理论保证，但它们是一个合理的使用模型。

实验

我们训练了对抗网络的一系列数据集，包括MNIST 、Toronto Face Database( TFD ) 和CIFAR - 10。生成器网络使用整流器线性激活ReL和sigmoid激活的混合物，而判别器网络使用maxout激活。Dropout被应用于训练判别器网络。虽然我们的理论框架允许在生成器的中间层使用dropout和其他噪声，但我们仅将噪声作为生成器网络最底层的输入。

我们通过对用$G$ 生成的样本拟合一个高斯Parzen窗并报告该分布下的对数似然来估计$p_g$ 下测试集数据的概率。高斯分布的$\sigma$ 参数是通过在验证集上的交叉验证获得的。这个过程是在Breuleux等人引入的，并用于精确可能性不可处理的各种生成模型。结果报告在表1中。这种估计似然的方法具有较高的方差，在高维空间中表现不佳，但它是目前已知的最好的方法。能够抽样但无法估计似然的生成模型的发展直接推动了如何评估此类模型的进一步研究。

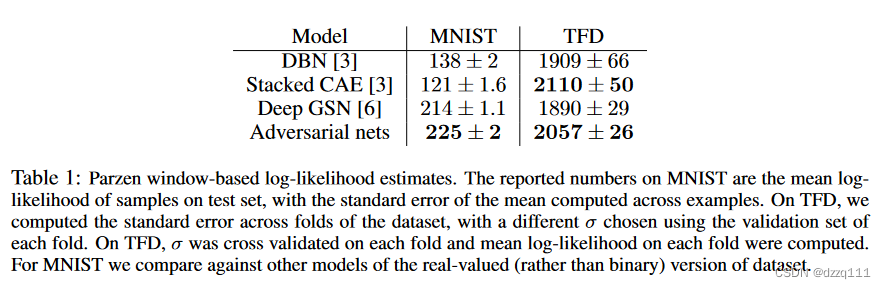
表一展示了模型基于Parzen窗的对数似然估计值。MNIST上的报告数是测试集上样本的对数似然值的平均值，标准误差是跨示例计算的平均值。在TFD上，我们计算了数据集不同折叠之间的标准误差，使用每个折叠的验证集选择不同的σ。在TFD上，对每个折线上的σ进行交叉验证，并计算每个折线上的平均对数似然值。对于MNIST，我们与实值(而不是二进制)版本数据集的其他模型进行了比较。

在图2和图3中，我们展示了从训练后的生成器网络中的样本。虽然我们没有声称这些样本比现有方法生成的样本更好，但我们认为这些样本至少与文献中更好的生成模型具有竞争力，并突出了对抗框架的潜力。

最右边一列显示了近邻样本的最近训练样本，以证明模型没有记忆训练集。样本是公平的随机抽取，而不是樱桃选择。与大多数其他深度生成模型的可视化不同，这些图像显示的是来自模型分布的实际样本，而不是给定隐单元样本的条件均值。此外，这些样本是不相关的，因为采样过程不依赖于马尔科夫链混合。

a ) MNIST b ) TFD c ) CIFAR-10 (全连接模型) d ) CIFAR-10 (卷积判别器和"反卷积"生成器)

全模型的z空间坐标之间通过线性插值得到数字。

优势和不足

这个新的框架与前面的模型架构相比也有优势和不足。不足主要是没有$P_g(x)$ 的显示表征，以及训练时D必须和G同步良好。特别是，在不更新D的情况下，G不能被训练得太多，以避免"无衬线字体场景"，在这种场景中，G将太多的z值崩溃到相同的x值，从而没有足够的多样性来建模$p_{data}$ 。就像玻尔兹曼机（Boltzmann）的负链必须在学习步骤之间保持最新一样。

框架的优势是马尔科夫链不再是必须的，只用了反向传播去获得梯度，在学习是推理也不是必须的。大量的函数可以被包含进模型中。表2总结了对抗生成网络和其他生成建模方法的对比。

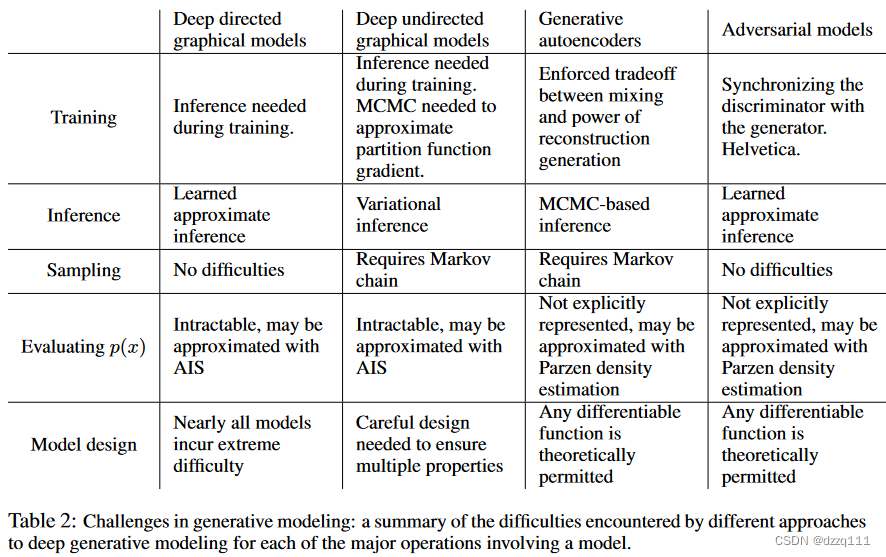
上述优势是主要是计算上的。对抗模型或许也能获得一些统计上的优势，因为生成器网络没有被直接使用数据样本更新，而是仅仅从判别器的梯度更新。这意味着输入的部分不是直接被复制到生成器的参数。对抗网络的另一个优势是他们可以表征非常尖锐甚至是退化的分布，而基于马尔可夫链的方法需要分布是有些模糊的，为了链能够在模式间混合。

结论及未来工作

1. 条件生成模型$p(x|c)$ 可以通过为G和D添加输入c获得。
2. 习得似然推理可以通过训练辅助网络去基于给定x预测z来实现。这类似于通过wake-sleep算法训练的推理网络，但是有一个优势是推理网络可能是在生成器网络已经训练完成之后才用一个固定的生成器网络训练。
3. 通过训练一组共享参数的条件模型，可以近似地对所有条件$p(x_S|x_{S/})$ 进行建模，其中S是x的索引的子集。本质上，可以使用对抗网络来实现确定性MP-DBM的随机扩展。
4. 半监督学习：当有限的标签数据是可用时，来自识别器或推理网络的特征可能改进分类器的效果。
5. 效率提升：训练可以通过选择更好的方法来协调G和D，或者在训练过程中确定更好的样本z分布，可以大大加快训练速度。

这篇论文证明了对抗建模框架的可行性，表明这些研究方向可能是非常有价值的。