第8章 空间解析几何与向量代数
8.1 向量及其线性运算
8.1.1 空间直角坐标系
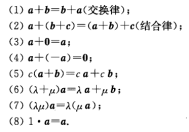
定理8.1
设向量a $ \neq $ 0,那么,向量a与b平行(记作a $ /!/ $ b)的充分必要条件是:存在唯一常数 $ \lambda $ 使得b= $ \lambda $ a.
共线算平行
标准基：
设a={ $ a_ {x} $ , $ a_ {y} $ , $ a_ {z} $ },则a= $ a_ {x}{1,0,0} $ + $ a_ {y}{0,1,0} $ + $ a_ {z}{0,0,1} $ = $ a_ {x} $ i+ $ a_ {yj} $ + $ a_ {z} $ k,这说明任意一个三维向量都可由i,j,k线性表示.我们把i,j,k称为 $ V_ {3} $ 中的一组标准基.
8.2 向量的数量积
8.2.1 向量的数量积
向量的夹角∈[0,π]
数量积【点积】【内积】(余弦)：
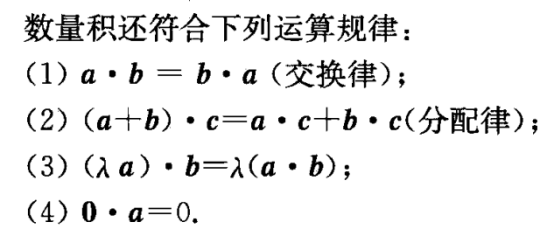
8.2.2 方向角、投影
方向角： cos 2 α + cos 2 β + cos 2 γ = a _ x 2 + a _ y 2 + a _ z 2 ∣ a ∣ 2 = 1. \cos^2\alpha+\cos^2\beta+\cos^2\gamma=\frac{a\_x^2+a\_y^2+a\_z^2}{\mid\boldsymbol{a}\mid^2}=1. cos2α+cos2β+cos2γ=∣a∣2a_x2+a_y2+a_z2=1.
{ $ \cos $ $ \alpha $ , $ \cos $ $ \beta $ , $ \cos $ $ \gamma $ }= $ \frac {a}{|a|} $ .
可见{ $ \cos $ $ \alpha $ , $ \cos $ $ \beta $ , $ \cos $ $ \gamma $ }正是与a指向相同的单位向量.
投影：
8.3 向量的向量积、混合积
8.3.1 向量的向量积
向量积【叉积】【外积】(正弦)：
8.3.2 向量的混合积
(
a
×
b
)
∙
c
=
a
∙
(
b
×
c
)
(a\times b)\bullet c=a\bullet(b\times c)
(a×b)∙c=a∙(b×c)
(
a
×
b
)
⋅
c
=
∣
a
x
a
y
a
x
b
x
b
y
b
z
c
x
c
y
c
z
∣
(a\times b)\cdot c=\begin{vmatrix}a_x&a_y&a_x\\b_x&b_y&b_z\\c_x&c_y&c_z\end{vmatrix}
(a×b)⋅c=
axbxcxaybycyaxbzcz
8.4平面及其方程
8.4.1 平面的点法式方程
A ( x − x _ 0 ) + B ( y − y _ 0 ) + C ( z − z _ 0 ) = 0. A(x-x\_{0})+B(y-y\_{0})+C(z-z\_{0})=0. A(x−x_0)+B(y−y_0)+C(z−z_0)=0.
法向量：(A, B, C)
平面上的点：(x, y, z) (x0, y0, z0)
如果线n和线a, b都垂直：则n= a × b
8.4.2 平面的一般式方程
Ax+By+Cz+D=0
通过x轴的平面，A=0，D=0
平行x轴的平面，A=0
8.4.3 平面的截距式方程
x
a
+
y
b
+
z
c
=
1
\frac xa+\frac yb+\frac zc=1
ax+by+cz=1
a,b,c依次是平面在x轴、y轴、z轴上的截距.
8.4.4点到平面的距离
注意到 $ P_ {1} $ ( $ x_ {1} $ , $ y_ {1} $ , $ z_ {1} $ )是平面上一点,所以 $ Ax_ {1} $ + $ By_ {1} $ + $ Cz_ {1} $ =-D,这样我们得到点
$ P_ {0} $ ( $ x_ {0} $ , $ y_ {0} $ , $ z_ {0} $ )到平面Ax+By+Cz+D=0的距离为
d
=
∣
A
x
0
+
B
y
0
+
C
z
0
+
D
∣
A
2
+
B
2
+
C
2
.
d=\frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{\sqrt{A^{2}+B^{2}+C^{2}}}.
d=A2+B2+C2∣Ax0+By0+Cz0+D∣.
8.5空间直线及其方程
8.5.2空间直线的对称式方程/点向式方程
x − x 0 m = y − y 0 n = z − z 0 p \frac{x-x_{0}}{m}=\frac{y-y_{0}}{n}=\frac{z-z_{0}}{p} mx−x0=ny−y0=pz−z0
举一个实例。把{2x+3y-4z+2=0;x+2y+3z-1=0化为对称式。
方法一:
平面2x+3y-4z+2=0的法向量为n1=(2,3,-4),
平面x+2y+3z-1=0的法向量为n2=(1,2,3),
因此直线的方向向量为v=n1 $ \times $ n2=(17,-10,1)
取x=10,y=-6,z=1,
知直线过点P(10,-6,1),
所以直线的对称式方程为(x-10)/17=(y+6)/(-10)=(2-1)/1。
问：两个一般/两个平面à对称式
解：
取交线上任意点
求两个面法向量n1,n2
nn=n1×n2
得到一个点+方向向量
n(A,B,C)
乘法：法向量 AX+BY+CZ+D=0
除法：方向向量
x
−
x
0
m
=
y
−
y
0
n
=
z
−
z
0
p
=
t
\frac{x-x_{0}}{m}=\frac{y-y_{0}}{n}=\frac{z-z_{0}}{p}=t
mx−x0=ny−y0=pz−z0=t
8.5.3空间直线的参数式方程
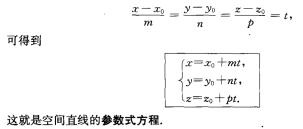
8.5.4 点到直线的距离
M1到l的距离
取l上任意一点M0，s是l方向向量，则有：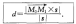
8.6 直线、平面之间的关系
8.6.1 两平面之间的关系
两平面/两直线之间的夹角不超过180度，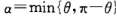
8.6.2.两直线之间的关系
8.7曲面及其方程
方程中已经有两轴，如(z, y)，问：绕z旋转，则：将方程中y方用x方+y方替代。
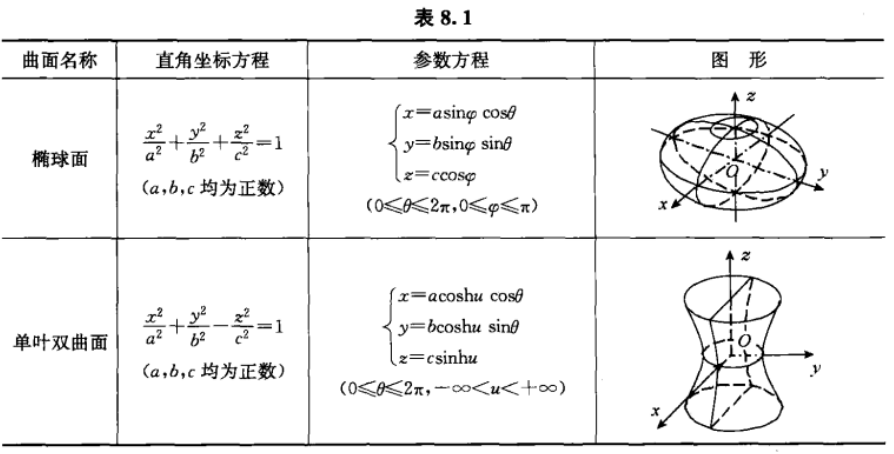
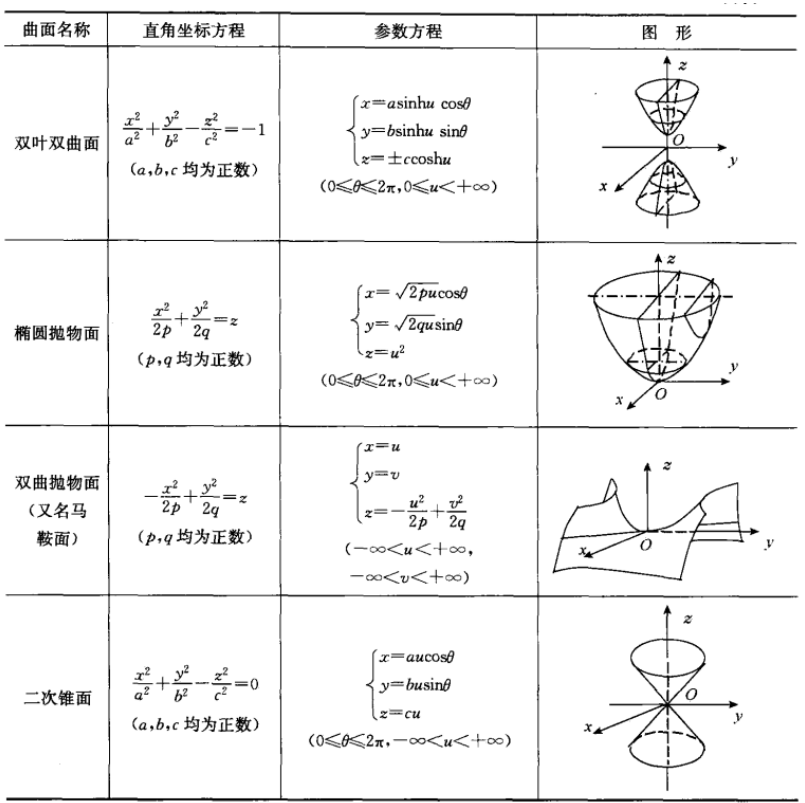
8.8 空间曲线和向量函数
8.8.1空间曲线及其方程
8.8.2 空间曲线在坐标面上的投影
8.8.3 向量函数确定的空间曲线
8.8.4 向量函数的导数和积分
7954
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
