Recommender Systems - Collaborative filtering algorithm

最新推荐文章于 2024-10-08 16:10:16 发布

王彩旗 edwardwangcq.com

最新推荐文章于 2024-10-08 16:10:16 发布

阅读量218

点赞数

分类专栏：人工智能 # 机器学习

本文链接：https://blog.csdn.net/edward_wang1/article/details/114084915

版权

人工智能同时被 2 个专栏收录

142 篇文章

订阅专栏

机器学习

109 篇文章

订阅专栏

Review of old Collaborative filtering

In the last few classes, we know that:

If you're given features for movies, you can use that to learn parameters $\theta$ for users

figure-1
If you're given parameters for the users, you can use that to learn features for movies

figure-2

One thing you could do is go back and forth. Maybe randomly initialize parameter $\theta$ , then solve for . Then solve for better $\theta$ , then better , and so on.

Optimized Collaborative filtering algorithm objective

I want to point out that the two square error terms in figure-1 and figure-2 are actually the same, that is:

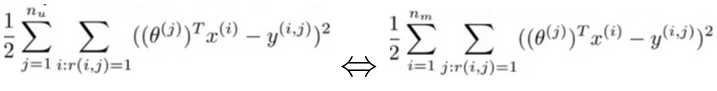
The left hand is sum over all users , and then sum over all movies rated by that user.
The right hand just does things in the opposite order. For every movie , sum over all the users that have rated that movie.

So both summations on the left and right hands are just summations over all pairs (i,j) for which r(i,j)=1 .

And thus, we have:

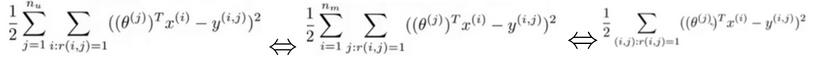
So we can define the following cost function by putting above two cost functions in figure-1 and figure-2 together:

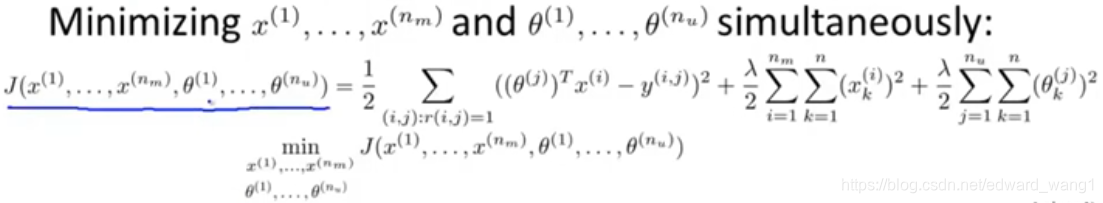
It actually has an interesting property:

If you were to hold the constant, then you'll be solving exactly the problem of figure-1
If you were to hold the $\theta s$ constant, then you'll be solving exactly the problem of figure-2

With the new cost function, instead of sequentially going back and forth between the two sets of parameters and $\theta$ , we'll just minimize with respect to both sets of parameters simultaneously.

Note:

With the new Collaborative filtering algorithm, we have $x\in \mathbb{R}^{n}$ by doing away with the intercept term $x_{0}$ which was set to 1 by convention. And similarly, $\theta \in \mathbb{R}^{n}$ . The reason is we're now learning all the features automatically. There is no need to hard code the feature that is always equal to 1. If the algorithm really wants a feature that is always equal to 1, it can choose to learn one for itself. The algorithm has the flexibility to just learn it by itself.

Optimized Collaborative filtering algorithm

Figure-6 shows the steps of Collaborative filtering algorithm. Firstly, we randomly initialize the feature $x^{(1)}$ and parameter $\theta ^{(1)}$ to some small values. Then minimize the features and parameters with GD or other advanced optimization algorithm. Then, suppose user has not rated movie yet, then the rating can be calculated as $(\theta ^{(j)})^{T}x^{(i)}$ .

<end>