模式识别（Pattern Recognition）学习笔记（十三）--多类线性分类器

模式识别（Pattern Recognition）学习笔记（十三）--多类线性分类器

如有错误还望海涵，谢谢。

引言

       在之前的学习和讨论中，均是围绕的两类问题来展开，但这毕竟不结合实际，实际应用中面临更多的往往是多类分类问题，如钞票代码识别中，10个数字的识别和26个英文字母的识别等。

       通常来说，解决多类问题的基本思路有两种：一是把多类问题分界成多个两类问题，通过多个两类分类器来时多类的分类；二是直接设计多类分类器。

多个两类分类器的组合

       为了便于讨论，我们拿一个三类的问题来举例，假设我现在有三类样本若干：男人，女人，人妖，为了解决这个三类问题的分类，我们可以有两种做法：第一个做法是，设计第一个分类器将男人和其他两类分开，第二个分类器把女人和其他两类分开，都不属于这两个分类器的就是人妖，哈哈；第二个做法是，先用两个分类器分别将男人和女人分开，男人和人妖分开，在用一个分类器将女人和人妖分开。

       第一种做法叫做“一对多（one-vs-rest或one-over-all）”，假如有c类样本，，就需要c-1个分类器就可以实现多类分类。但是，这种做法有两个弊端，一方面，当各类样本数量差不多的时候，这种做法就很容易出现两类样本数量失衡的现象，而这一现象可能会严重导致分类错误发生在样本数小的一类上，毕竟有监督分类问题的正确率是跟样本数量有着一定关系的，这个时候我们需要采取适当的修正措施来补救。另一方面，用c-1个分类器就是要有c-1个分类超平面，从而将样本所在的特征空间分成c个区域，但是在一般情况下，这种划分不会恰好得到c个区域，而是会多出来一些区域，因此会在分类过程中造成歧义，如图（左）阴影部分被称为分类盲区或歧义区。

       第二种做法叫做“逐对分类（pairwise）”，主要是对多类中的每两类进行分类，因此这种做法需要构造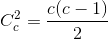个分类器，明显比上一种做法使用的分类器要多，但是这种做法不会出现一对多中的样本失衡问题，而且分类过程出现的盲区也会比一对多的要少一些，可以从上图（右）看的出来。

       上面介绍的两种做法中，并没有对分类器做具体的指出，只是假设每个分类器会给出样本属于哪一类别的决策，实际上，很多分类器在最后决策前都会给出一个连续量，最后的分类结果也正是对这个连续量与一个预设阈值比较的结果，例如前面学习的所有线性分类器都被转化为一个判别函数与某一阈值进行比较的问题。

       在很多线性分类器中，一个正确分类的样本，如果它距离分类面越远，则往往对它的类别决策就更加确定，因此我们可以把分类器的输出看作是对样本决策的一种打分机制，score越高决策越确定。于是，对于c类问题，我们可以对每一类都设计一个分类器，即c个分类器；决策时，如果只有一个分类器的输出大于给定阈值，其他分类器的输出都小于阈值，那么就把这个样本决策为大于的那一类。进一步，如果每个分类器的输出是可比的，并且根据类别的定义知道任意样本必定属于且只属于某一类，那么可以在决策时直接比较各分类器的输出值，最后把该样本划分到输出最大的那个分类器对应的类中去，但是需要注意的是，如果分类器是分别训练的，那么输出就不一定存在可比性，这个时候就要具体情况具体分析。

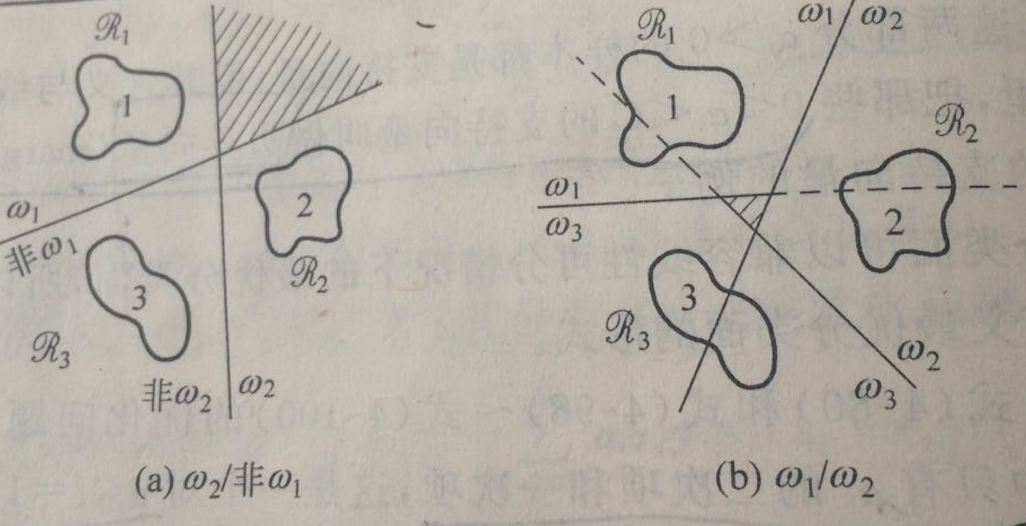
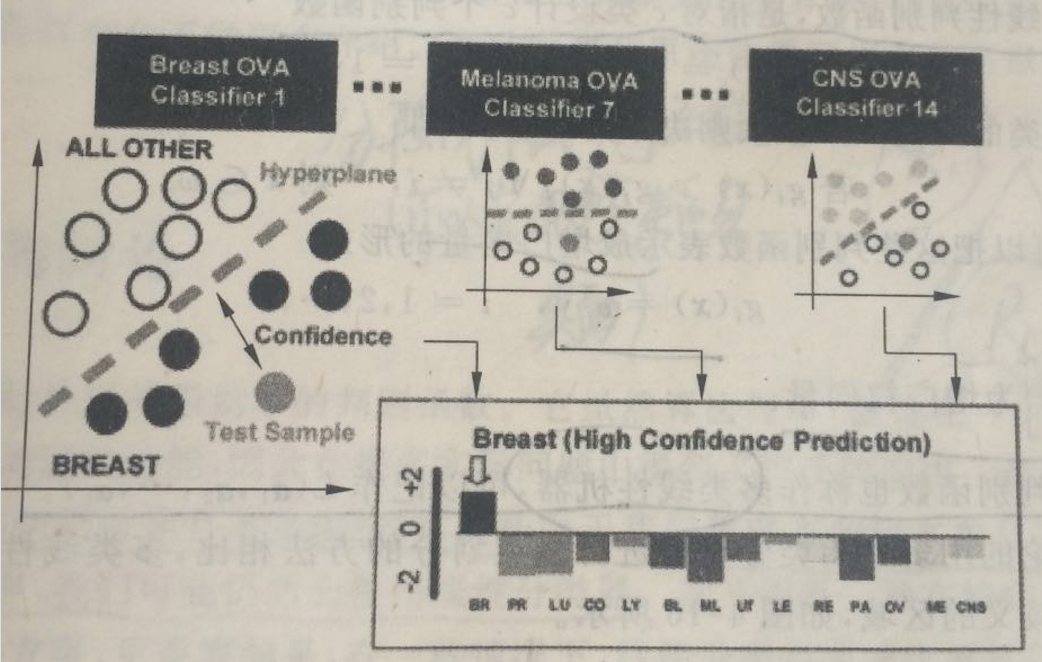
       可以看一个例子，是用多个SVM来对14类癌症基因数据的一个分类，最后也是将样本划分到输出最大的分类器对应的类别，如图：

       注意，因为SVM训练中需要调整w的尺度以达到最大间隔，且不同的两类问题训练后的尺度也并不是完全相同，有时候会差别很大，所以这样得到的多个SVM的输出并不能严格保证可比，但这个例子中，各SVM的尺度差别并不是很明显，所以可以直接比较。