GPU上并行处理大规模粒子系统
原文:[Latta04] Luta Latta, "Massively Parallel Particle Systems on the GPU Latta," <<ShaderX3>> 2004
作者:Lutz Latta
本文版权归原作者所有,仅供个人学习使用,请勿转载,勿用于任何商业用途。
翻译:fannyfish
Blog:http://blog.csdn.net/fannyfish
amma@zsws.org
介绍
现实世界中充满了不规则运动的小物体。人们设计物理正确的粒子系统(PS)来模拟这些自然现象。过去几十年里,粒子系统被广泛地应用在即时渲染和预渲染(如影片、广告)领域来模拟不同的体积特效。
粒子系统在游戏与计算机图形学领域中有很长的历史。早在1960年,已经有游戏使用2D象素的烟雾来模拟爆炸。第一篇讲解粒子系统的计算机图形学论文 [Reeves83],是在卢卡斯影业完成了电影
《星际迷航
II
》的特效制作后诞生的。Reeves先生在论文里描述了粒子的基本数据实现和运动模拟方法――这两个概念一直延用至今。随后,[Sims90]提出了针对超级计算机上多个并行处理器的解决方案。本文用到了许多他和[McAllister00]提出的模拟速度、位置的方法。最近一篇描述基于CPU的粒子系统的论文是[Burg00]。
即时粒子系统的性能主要受两个因素制约:填充率(fillrate)或CPU-图形硬件(GPU)之间的数据传输带宽。填充率即GPU每帧可以渲染的象素数,当粒子很大并且出现好多粒子重叠在一起的情况时会严重影响性能。由于使用更多更小的粒子能达到更好的模拟效果,填充率在粒子模拟中变得越来越不重要了。因此,从负责模拟的CPU到负责渲染的GPU之间的传输带宽决定了系统性能。一般来说,在游戏程序里同时被其它渲染任务使用的图形总线(Graphics bus)仅允许基于CPU的粒子系统每帧处理10,000个粒子。为了最小化粒子数据传输,可以在GPU上将模拟和渲染集成在一起处理。
在考虑实现基于GPU的粒子系统之前,首先要了解状态无关(stateless)和状态相关(state-preserving)粒子系统这两个概念。状态无关PS,指仅通过一个由粒子初始属性和当前时间定义的闭合函数来计算粒子数据。状态相关PS,指根据上一帧的粒子属性和环境变化(如移动了碰撞体),使用数值计算和迭代积分来计算粒子数据。这两种模拟方法有各自的适用领域,需要根据模拟特效的不同做出选择。
[NVIDIA01]介绍了基于PC第一代可编程GPU的状态无关PS,下一节将做简单的描述。随着硬件发展,在当今的浮点图形硬件上实现状态相关PS也成为可能,随后的章节将主要阐述其实现。其中GPU的粒子物理模拟可以灵活地组合多种运动和位置操作,如重力、局部力和与几何图元或高度图的碰撞。另外,为了得到正确的alpha-blended渲染结果,还将使用一种平行的排序算法按照距离对粒子进行排序。
状态无关粒子系统
[NVIDIA01]介绍了使用Vertex Shader(也叫做Vertex Program)实现PS的方法。这种PS是状态无关的,也就是说,它没有存储粒子的当前位置等属性。要计算粒子位置,你必需找到一个由粒子初始属性和当前时间定义的闭合函数。因此,状态无关PS很难对动态环境做出反应。
粒子不能和环境碰撞,而只能通过简单函数来实现受到重力加速度g的影响:
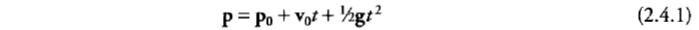
p 是粒子位置的运算结果,p0代表初始位置,v0代表初速度,t指当前时间
。如果想加上简单的碰撞和局部力的影响,则需要复杂的多的函数。
除位置和速度以外的其它粒子属性(例如,粒子朝向、大小和纹理坐标)的计算规则更为简单,一般只需根据粒子存活时间累加一个常量。在下面章节中,尽管位置使用状态无关模拟,这些属性还是使用状态相关来模拟。
状态无关PS的特点决定了它适合模拟少量简单与环境无关的效果。例如动作游戏中的武器击打效果,水花或碰撞火花。
图形硬件上的粒子模拟
以下各节详细讲述GPU上的状态相关粒子系统。首先简要介绍算法,然后具体闸述粒子的存储方式和处理过程。
算法综述
状态相关粒子系统使用纹理存储粒子的位置和速度。这些纹理同时也是RenderTarget。在一个渲染通道里,根据上一时间戳的速度计算并更新速度纹理。更新过程执行一步迭代积分来计算加速度力和碰撞反射。另一个渲染通道使用类似的方法更新位置,利用上个通道求得的速度对位置求积。根据所选的积分方法不同,有可能跳过更新速度通道,直接通过加速度对位置求积。
为了避免渲染走样,可以选择将位置纹理的数据按照与摄像机的距离排序。排序算法将额外占用几个渲染通道来处理包含距离数据的纹理。
接下来将位置纹理转换成Vertex Buffer。最后按照传统的方法绘制这些几何数据――做为点精灵,三角形或方形。
整个算法可以分为以下六个基本步骤,后面小节将一一闸述:
1,处理生存和死亡
2,更新速度
3,更新位置
4,为alpha blending进行排序(可选)
5,将纹理数据变换为顶点数据
6,渲染粒子
粒子数据存储
粒子最重要的属性是位置和速度。我们使用一张浮点纹理存储所有粒子的位置,颜色分量分别保存x,y,z坐标。可以把这张纹理当成一维数组,其中纹理坐标代表数组索引。由于硬件支持的纹理大小有限制,通常使用二维纹理来表示更大的数组。纹理同时也被定义为RenderTarget,以确保能保存动态计算的位置数据。通过渲染一个全屏的方形(quad),GPU会为RenderTarget上每个象素调用一次Pixel Shader。Pixel Shader需要从位置纹理中读取上一帧的位置。因为不能同时读取和渲染一张纹理,我们使用双缓存技术--创建两张纹理存储上帧数据和新数据。
速度纹理可以使用类似的方法创建。由于速度对精度要求较低,纹理可以使用16位浮点格式。根据使用积分算法的不同,有可能不需要显式地(explicitly)存储速度(见126页)。这时需要使用三缓存技术,创建第三张位置纹理。
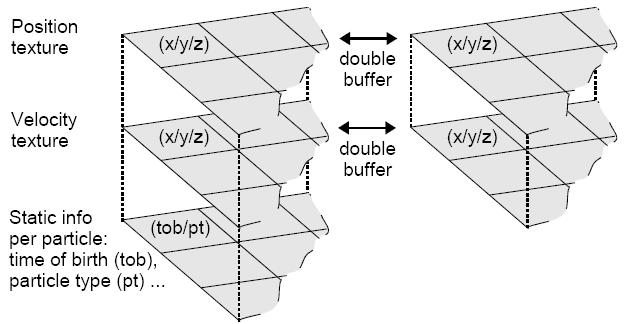
图2.4.1 用多张纹理存储粒子数据。
如果使用迭代积分方法处理粒子的其它属性(如朝向,大小,颜色和透明度),那么也需要创建双缓存纹理。然而这些属性通常只需要简单的计算规则甚至可能是静态值,我们可以使用与状态无关粒子系统类似的方法处理(见120页),根据粒子的生存期以一个函数来描述(例如,使用初始值和微分值或者一系列关键帧)。为了执行此函数,需要创建额外的纹理来存储每个粒子的两个静态数值:生存期和粒子类型相关的属性参数。
为了减少渲染粒子前更新静态属性参数的数量,我们假设可以根据粒子类型对粒子分组。例如规定一个粒子发射器为一种类型或一组发射器发射的粒子为一种类型。
粒子质量用来计算外力的加速度。它有两种存储方法:一是假设所有粒子的质量相等,将质量或其函数作为粒子类型参数上传,二是将每个粒子的质量保存在上面提到的静态纹理中。
综上所述:不同纹理使用同一纹理坐标存储同一粒子的不同属性。根据需要,可以使用粒子类型参数计算其它属性。
处理生存期
粒子可能永久存在也可能只存活一段时间。所有粒子都永久存在是最容易模拟的情况,因为只需要向属性纹理更新一次初始值。但这种情况毕竟很少见,后面章节的讨论只针对粒子有有限生存期的情况。这意味着粒子系统必需处理粒子的出生--分配(allocation)和死亡--释放(deallocation)。
刚出生的粒子需要使用属性纹理的合法索引来关联新数据。从本质上讲分配问题是连续的,而GPU不能实现高效地数据并行分配算法。因此我们选择在CPU上使用传统的快速分配表产生合法索引。最简单的分配策略,是将所有合法索引压入一个栈里。相对复杂的分配器使用优化过的堆结构,以保证总是返回最小的合法索引。对于模拟粒子数目高度变化的情况,这种分配器可以确保存在的粒子总是集中在堆前面的数据段,随后的模拟和渲染步骤可以只操作这段数据。成功得到索引后,将新的粒子数据作为一个象素渲染到属性纹理,CPU可以用复杂的算法决定这个初始数据,例如,使用不同的概率分布决定初始位置和速度。
粒子的死亡由CPU和GPU分别处理。CPU通知分配器粒子已死,并标记此索引为可分配。GPU使用一个额外的通道,由生存期和已存活的时间来决定生死。将已死亡粒子的位置移到不可见区域,如无穷远。因为粒子在生命快要结束时通常是慢慢消失或已脱离了可见区域,为了提高效率可以不使用处理死亡的渲染通道,取而代之的是一步clean-up操作。
更新速度
运动模拟的第一部分是更新粒子速度。通过渲染一个全屏的方形,GPU为RenderTarget上每个象素执行一次Pixel Shader来更新速度。首先设置双缓存的其中一张速度纹理为当前RenderTarget,然后从另一张纹理中读取上一时间戳的速度。其它所需数据可以从属性纹理或Shader执行前设置的常量中获得。
多种速度操作可以按需组合(见[Sims90]和[McAllister00]):全局力(如重力,风力),局部力(如引力,斥力),速度阻力和碰撞反射。我们将这些参数保存到常量寄存器中。动态混合操作是即时图形学的经典问题,这里可以使用光源与材质混合的类似解决方案。使用多个通道处理其它操作。
全局力如重力,总是在某个方向上使粒子受一个固定加速度影响。局部力则是根据从位置纹理读出的上一帧位置来影响粒子。假设粒子受一个磁铁影响,这相当于使粒子受一个指向某点的局部加速度影响。这个力的大小与粒子到磁体的距离的平方成反比,或者在某个距离之内为常量(请参考[McAllister00])。假设粒子的加速度总是指向直线上某一点,同时这个点是直线上与粒子距离最近的点,那么就能实现涡流效果。
使用流场纹理可以实现更复杂的局部力。因为GPU的纹理查找操作代价低廉,将包含流场速度向量的2D或3D纹理映射为粒子位置非常高效。采样得到的流场速度向量Vfl带入斯托克斯公式救出小球受到的外力:
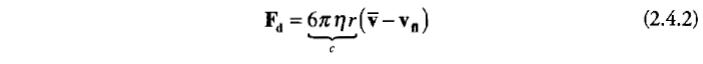
公式中
η
为粘滞系数,
r
为小球的半径(这里指粒子),v
代表粒子的运动速度。可以将这些常量保存在一个常量寄存器中以便操作。
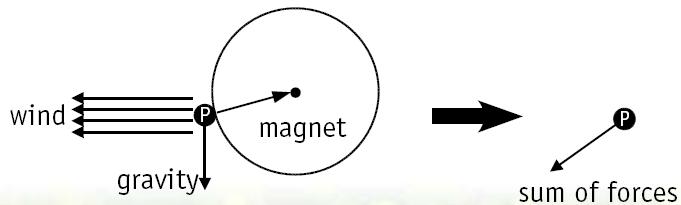
图2.4.2 将多个力组合成一个力向量。
将全局和局部力组合成一个力向量,如图2.4.2。然后根据牛顿定律计算出加速度:
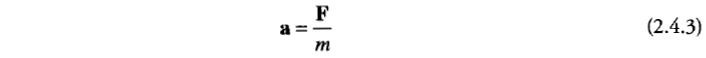
其中a是加速度向量,F是累加起来的力,m为粒子质量。假设所有粒子都是单位质量,则可以忽略此步计算,直接将力当作加速度使用。
接下来用简单的欧拉角积分公式求速度:

V是粒子当前速度,v是上一时间戳的速度,t是时间戳。
阻尼是另外一种速度操作,通常指粘性材质或空气阻力对原有速度的缩放影响。这是公式
2.4.2
在流场速度为
0
时的特例。阻尼的相反操作,可以用来模拟自力推进物体,如蜂群。
碰撞也是一种重要的操作。
GPU
的优势不在于处理与平面或球体的简单碰撞上,而在于处理粒子与高度图描述的地形进行碰撞。通过采样高度图的三个点计算出法向量,然后根据法向量得到反射向量。法向量也可以使用缩放过的法线贴图(
Normal map
)来存储。注意,可以用类似于
Shadow mapping
的算法将物体的深度值渲染到纹理中,动态生成高度图。这样可以用多张高度图近似实现与复杂几何体的碰撞。这种技术的具体细节请参考
[Kolb04]
。
在检测到碰撞后,开始计算碰撞反射也就是计算碰撞后的速度(参考
[Sims1990]
)。首先将当前速度分割成水平和垂直分量。假设
n
是碰撞点的法向量,下列公式用于计算分量:
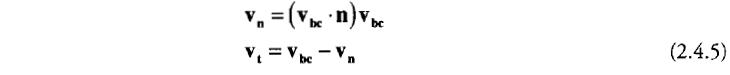
Vbc其中
是碰撞前的速度,Vn
是此速度的垂直分量,Vt
是水平分量。两个分量可以分别和两个材质属性做运算。动态摩擦力
η
影响水平分量,弹性系数ε
决定垂直分量。碰撞后的速度这样计算:

这种方法存在两个会引起渲染走样的问题。因为碰撞是在处理加速度外力之后发生的,动态摩擦力最终会使速度等于(非常接近)
0
,最终导致粒子悬浮在空中。解决此问题需要指定一个阈值,当速度小于此值时就不再改变。
第二个问题是粒子会穿入碰撞体内部。棱角分明的碰撞体(如高度图)或两个相距很近的碰撞体会导致这种情况发生。
解决方法是捕获这种粒子并将其放到碰撞体外。通常的方法是:做一步积分预测粒子下一时间戳的位置,然后检测碰撞(见图
2.4.3a
)。预测出的粒子位置
这样计算:
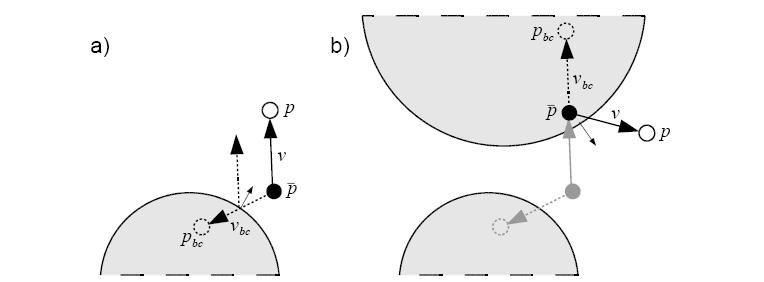
图
2.4.3
粒子碰撞:
a)
普通的碰撞检测
b)
两次碰撞,避免粒子进入碰撞体。
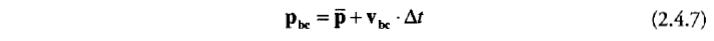
Pbc是上一时间戳的位置。如果做两次碰撞就能避免粒子进入碰撞体内部,第一次用上一时间戳的位置第二次用下一时间戳的位置,此时需要区分将要碰撞和已经碰撞过两种情况(见图
2.4.3
b
)。如是后者则立即或保持原有速度将粒子弹出碰撞体。根据法向量可以判断出如何如何计算速度:

更新位置
运动模拟的第二部分是更新粒子位置。本节将详细讨论前面提到的各种积分方法(见121页)。在GPU上处理海量数据时只能使用简单的积分算法。适合粒子模拟的有欧拉(Euler)积分和Verlet积分。
上一节根据加速度求速度时已经使用过欧拉积分。已知计算过的速度求位置可以用相同的方法:
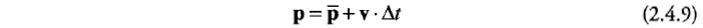
p和p'分别代表当前位置和上帧位置。
在某些方面Verlet积分比欧拉积分更简单(请参考[Verlet67])。使用Verlet积分的粒子系统不用显示地存储速度(参考[Jakobsen01]),而只需存储两个时间戳之前的位置。这带来的最大好处在于减少了显存消耗和节剩了速度更新通道。
假设时间戳是常量,得到的位置计算公式只和加速度有关:

其中p是两个时间戳之前的位置。可以看出,Verlet积分可以高效处理简单的加速度(全局和局部)。然而对于像碰撞反射这种复杂的速度操作就不同了,这要求在碰撞后执行能隐式改变速度的位置公式。有一种高效的解决方案是设置位置约束(position constraints),碰撞时只需简单地把位置移出碰撞体。由于约束了运动,推导速度时将隐式地引入反射速度。还可以为两个粒子或两团粒子之间加一些约束,用来实现布料或头发的粒子模拟([Jakobsen01]有详细闸述)。
根据Alpha Blending排序
(
未完成
)
将纹理数据变换为顶点数据
将纹理数据考备为顶点数据是近期的PC GPU才支持的硬件特性。目前有两种方法可以实现:
DirectX和OpenGL分别通过Vertex Shader(VS) 3.0(请参考[Microsfot02])和ARB_vertex_shader扩展(请参考[OpenGL03])提供了Vertex Textures特性。要使用Vertex Textures渲染粒子,需要创建一个静态Vertex Buffer,它存储着位置纹理所有象素的纹理坐标。当渲染这个VB时,Vertex Shader根据它记录的纹理坐标从纹理中读出粒子位置(见图2.4.5)。现在的硬件从Vertex Textures中读取数据有很大延迟,也就是说,从发出纹理读取指令到返回纹理值的时间很长。幸运的是在等待期间可以做一些和纹理值无关的数值操作。幸运的是粒子系统的Vertex Shader中有很多与粒子位置无关的操作要做(请参考131页),这弥补了纹理读取带来的效率问题。

图2.4.5,为了渲染粒子需要在Vertex Shader中访问纹理。
也可以使用“über-buffers”(也叫做super buffers,请参考[Mace04])来实现,它可以存储顶点或象素数据。这个概念随着第一代浮点GPU产生并延用至今,但是只有OpenGL API支持。OpenGL提供的EXT_pixel_buffer_object扩展(请参考[NVIDIA04])提供了GPU内的快速异步考备数据。因为可以将象素数据考备到顶点流(见图2.4.6),这也是实现über-buffer的基本概念。

图2.4.6 使用uber-buffer概念将象素数据考备到顶点数据。
粒子可以渲染为点精灵,三角形或方形(见131页)。如果Vertex Textures只用做数据传输,则它不用负责使用哪种几何类型。如果每个粒子需要多个顶点,可以简单地将静态VB中包含每个粒子的纹理坐标重复3或4次。或者使用VS3.0支持的“Vertex stream frequency”特性。这种技术可以减少传给Vertex Shader数据的更新频率。顶点流的一块数据可以被一系列连续的顶点使用,而其它顶点流按照一定的频率更新。所以对于粒子来说,Vertex Buffer不需包含重复数据,而只需设置更新频率(三角形为3,方形为4)。
在不支持Veretx Texture或Vertex stream frequency特性的硬件上,使用über-buffer要求在渲染前手动重复存储粒子位置。在渲染阶段,一个象素会被重复写3或4遍。从效率考虑,现在的实现使用一个粒子对应一个顶点的点精灵。
渲染粒子
最后按传统方法,用转换来的顶点位置在帧缓存上渲染图元。上节提到过,为了降低顶点单元的负载,选择点精灵来渲染粒子。和使用三角形或方形相比,这节省了3或4倍的顶点数。然而使用点精灵的缺点是粒子总是轴对齐的,不能绕着z轴做2D旋转。为了战胜这个缺点,我们通过在Pixel Shader里旋转纹理坐标来实现二维旋转。使用点精灵还是三角形/方形取决于特定程序在顶点和象素单元上的负载。
渲染过程中,通过粒子类型参数(见121页)计算其它属性(如颜色和大小)。使用粒子生存期或伪随机函数来计算这些属性。
现在的实现使用下列规则计算粒子属性:粒子大小在粒子类型定义的范围中取随机值。初始角度和旋转速度(屏幕空间的二维值)也是在粒子类型定义的范围中取随机值。
粒子的颜色和透明度需要根据生存期在4个关键帧之间插值得到。每种粒子类型可以定义4个不等距的关键帧。需要在GPU上实现三个线性函数公式来处理粒子类型数据。
渲染时不能在逐象素处理过程中更换纹理,因此只能把不同的纹理组合成一张2D纹理。这样每个粒子需要选择合适的纹理坐标。如果使用点精灵,光栅化时会自动将纹理坐标变换到[0-1]x[0-1]的范围内。这时需要在Pixel Shader里选择子纹理。幸运的是,上面介绍2D旋转使用的纹理坐标变换可以免费实现子纹理的选择操作,因为使用2x2或3x2的矩阵变换都需要2个向量操作。
结论
当然现在处理器的速度还不够快。在最新一代GPU上,模拟并即时渲染1024x1024的粒子纹理时只能启用很少的效果并且关闭排序。开启全部效果只能处理512x512个粒子。下一代图形显卡应该会有另人期待的性能提升。
本文讲解了在当今可编程图形硬件上如何设计和实现一个状态相关的、物理正确的粒子系统。模拟过程可以使用欧拉或Verlet积分更新粒子位置,使用相对简单的算法处理其它粒子属性,并且只有在需要的时候才执行这些计算。另外还介绍了一种高效的并行排序算法。
基于GPU粒子系统的最大优点在于对整个数据集的单步操作非常高效。一旦完成了基本框架,就可以轻松地使用HLSL实现无穷无尽的算法来处理速度和位置。
虽然本文介绍的状态相关粒子模拟对即将发布的下一代电视游戏机(video game console)是否适合还有待考查。但是在多处理器硬件日新月异的今天,并行处理的粒子系统将发挥出重大价值。
致谢
(省略。)
索引
[Batcher68] Batcher, Kenneth E., “Sorting Networks and their Applications,” Spring Joint Computer Conference, AFIPS Proceedings 1968.
[Burg00] van der Burg, John, “Building an Advanced Particle System,” Game Developer Magazine(03/2000).
[Jakobsen01] Jakobsen, Thomas, “Advanced Character Physics,” GDC Proceedings
http://www.gamasutra.com/resource_guide/20030121/jacobson_pfv.htm, 2001.
[Kolb04] Kolb, Andreas; Latta, Lutz; Rezk-Salama, Christof, “Hardware-based Simulation and Collision Detection for Large Particle Systems,” Graphics Hardware Proceednigs 2004.
[Lang03] Lang, Hans W., “Odd-Even Merge Sort,” available online at
http://www.inf.fh-flensburg.de/lang/algorithmen/sortieren/networks/oemen.htm
[Mace04] Mace, Rob, “OpenGL ARB Superbuffers,” available online at
http://www.ati.com/developer/gdc/SuperBuffers.pdf, 2004
[Mark03] Mark, William R.; Glanville, R. Steven; Akeley, Kurt; Kilgard; Mark J., “Cg: A System for Programming Graphics Hardware in a C-like Language,” SIGGRAPH Proceedings 2003.
[McAllister00] McAllister, David K., “The Design of an API for Particle Systems,” Technical Report, Department of Computer Science, University of North Carolina at Chapel Hill, 2000.
[Microsoft02] Microsoft Corporation, “DirectX9 SDK,” available online at
http://msdn.microsoft.com/directx/, 2002-2004.
[NVIDIA01] NVIDIA Corporation, “NVIDIA SDK,” available online at
http://developer.nvidia.com/, 2001-2004.
[NVIDIA04] NVIDIA Corporation, “OpenGL Extension EXT_pixel_buffer_object,” available online at
http://www.nvidia.com/dev_content/nvopenglspecs/GL_EXT_pixel_buffer_object.txt, 2004.
[OpenGL03] OpenGL ARB, “OpenGL Extension ARB_vertex_shader,” available online at
http://oss.sgi.com/projects/ogl-sample/registry/ARB/vertex_shader.txt, 2003.
[Reeves83] Reeves, William T. “Particle Systems—Technique for Modeling a Class of Fuzzy Objects,” SIGGRAPH Proceedings 1983.
[Sims90] Sims, Karl, “Particle Animation and Rendering Using Data Parallel Computation,” SIGGRAPH Proceedings 1990.
[Verlet67] Verlet, Loup, “Computer Experiments on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules,” Physical Review(159/1967).






















 470
470

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








