CRF基本介绍
在机器学习中,建模线性序列结构的方法,除了HMM算法,另一个重要的模型就是CRF。HMM为了降低模型复杂性,对观测变量做了独立假设(即隐状态之间有相关性,而观测变量之间没有相关性),这在某种程度上损害了模型的准确性;CRF弥补了这个缺陷,它同样假设类别变量之间有相关性,但没有对观测变量之间做出任何假设(即可能有相关性,也可能没有相关性)。
CRF除了和HMM形成对比,前者是判别式模型,后者是生成式模型;另一方面,CRF还可看成是对最大熵模型的扩展,即它是一个结构化学习模型,而不是单个位置的分类模型。CRF如何被因子化,CRF公式如何推导,如何建立最大熵模型和CRF的公式联系,以及如何得到CRF图表示结构是本文的几个重点。本文还会提到,一些算法,刚开始被用于HMM,稍作修改也能用于线性链CRF,比如前向-后向算法、维特比算法。另外需要指出,用于线性链CRF的训练和推理算法,不能直接用于任意结构的CRF。
背景知识:条件熵(Conditional entropy)
信息论中,条件熵用于量化描述随机变量Y所需的信息量,在另一个随机变量X已知的情况下,写作H(Y|X),具体形式如下:
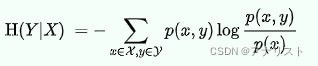 (公式1)
(公式1)
其中和
![]() 表示随机变量X和Y的样本集。注意,这里有可能出现
表示随机变量X和Y的样本集。注意,这里有可能出现,可以认为等于0,因为
![]()
直觉上,可以把看成是某个函数
的期望,即
,其中
是条件概率,被定义为:
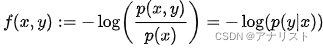
它是公式1中负号放到求和里面后的右半部分。
函数可看成当给定变量
时,为描述变量
需要的额外信息量。因此通过计算所有的
数据对的
期望值,条件熵
就能测量出要想通过
变量解码出
变量,平均意义上需要多少信息。
现在进一步要问,以上具体怎么来的?首先假设Y的概率密度函数为
,那么Y的熵
就是
,具体为:
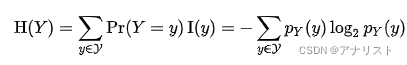 (公式2)
(公式2)
其中是当Y取
的互信息。因此,已知X为某个取值x时求Y的熵
根据条件期望,即代入公式2有:
 (公式3)
(公式3)
注意,表示对
求关于所有不同x取值的平均。换言之,
是对
关于每个x的加权求和,其中权重就是概率
,具体如下:
 (公式4)
(公式4)
上式第1个等号根据定义;第2个等号使用了公式3;第3个等号调整,将两个合并简化;第4个等号利用贝叶斯公式。公式4最后得到公式1。
一些基本属性:当且仅当Y完全被X控制。
当且仅当Y和X是两个独立的随机变量。
条件熵的链式规则:,即当X的熵
已知,那么Y的条件熵
可通过联合熵
减去
得到。它的推导过程如下:
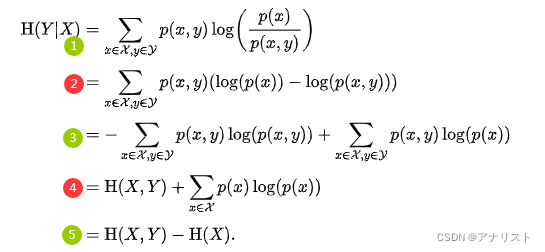 (公式5)
(公式5)
上式第1步来自公式4;第2步把log拆成相减的两项;第3步把拆成两项;第4步对第一项套用熵的公式得到
,对第二项消去y变量(对y求和);第5步继续套用熵的公式,得到
把公式5扩展到多个随机变量,得到:
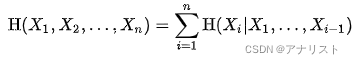 (公式6)
(公式6)
可以发现公式6和概率中的链式法则类似,只不过把乘法变为了加法。
条件熵的贝叶斯规则:,证明如下:因为有
,以及
,别忘了
,得证。特别的当Y条件独立于Z(当给定X),那么有
最大熵模型(Maximum Entropy Model)
最大熵模型是一个条件概率模型,它基于最大熵原则,意思是,当我们不具备对一个概率分布的完整信息时,唯一的无偏估计假设就是均匀分布。在该假设下,最恰当的概率分布就是在给定约束下的最大化熵的分布。根据公式1,对于条件模型,对应的条件熵
为:
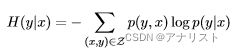 (公式一)
(公式一)
其中Z = X ×Y ,包含了所有可能的输入x和输出y。注意:Z不仅包括所有训练数据的样本,也包括所有可能出现的组合。最大熵模型的基本原理是:找到使得条件熵
取得最大值,但仍然符合训练数据中的约束信息。目标函数(也叫主问题,即primal problem)如下:
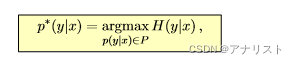 (公式二)
(公式二)
其中P是满足训练数据约束条件的所有模型的集合。
我们假设训练样本体现为特征。现在定义二值特征函数(其中
),它既依赖输入变量x,也依赖类别变量y,一种可能的函数形式如下:
 (公式三)
(公式三)
每个特征的期望值是从经验分布
估计得到,而经验分布是通过对训练集中不同值的频率进行简单计数得到,具体表达式如下:
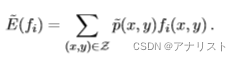 (公式四)
(公式四)
注意,所有可能的数据对都被统计在内。考虑到所有不被包含在训练集中的数据对
的经验概率为0,公式四可以改写为:
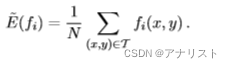 (公式五)
(公式五)
其中N是训练集的大小,即。因此
可通过对训练数据(
)统计
为1的频率计算得到,当然要除以训练集大小N。
类似于经验分布的特征期望值(即公式四),模型分布的特征期望值为:
 (公式六)
(公式六)
注意,由于所有可能的取值非常大,
可能无法简单计算。因此可对
重写:
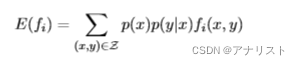 (公式七)
(公式七)
以上把联合概率变为了条件概率乘积。进一步,我们把替换为经验分布
,就得到了
的近似值:
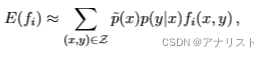 (公式八)
(公式八)
类比公式五,上式可进一步转化为:
 (公式九)
(公式九)
注意,上式只有出现在训练集中的x被考虑(),以及所有的y取值都被考虑(
)。很多应用中y的取值只有很少几个可能值,因此对所有y求和是可行的,
可以被高效计算。
公式二假设最优模型和训练数据一致,这意味着每个特征
在经验分布上的期望值和在特定模型分布上的期望值等价,即有:
![]() (公式十)
(公式十)
另一个约束是,对于条件概率恒有:
 (公式十一)
(公式十一)
在特定约束下的最优化问题,可以用拉格朗日乘子法解决,对每个约束引入
,得到如下拉格朗日函数
:
 (公式十二)
(公式十二)
求解过程如下:
首先与公式八的期望值近似求解类似,公式一的的近似求解为:
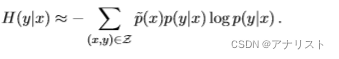 (公式十三)
(公式十三)
上式对的偏导为:
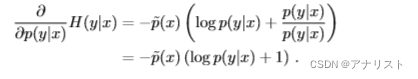 (公式十四)
(公式十四)
说明:把看成变量,把
看成常量,相当于对xlogx的形式求导数,比较简单。
公式十二的第二部分,即前m个约束,对的偏导为:

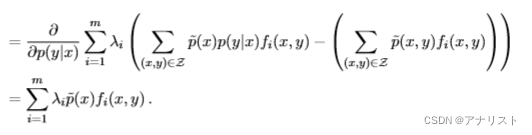 (公式十五)
(公式十五)
以上分别将和
的表达式(即公式八和公式四)代入,注意,减号右边不包含
,因此偏导为0,而左边是
的线性函数,只需保留其余系数即可。
公式十二的第三部分更简单,它对的偏导就是系数
,因此完整的偏导如下:
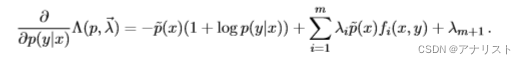 (公式十六)
(公式十六)
令上式为0,来求解,得到:

移动右边第一项到左边,得到:
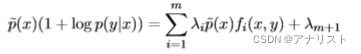
等式两边除以,得到:
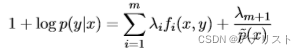
把上式的1移到右边,得到:

把log消除,得到的表达式:
 (公式十七)
(公式十七)
考虑到公式十一有个概率加和约束:
 (公式十八)
(公式十八)
我们把公式十七代入公式十八,得到:
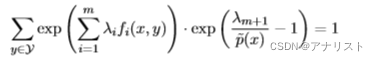
等式两边除以左边第一项,得到:
 (公式十九)
(公式十九)
把公式十九重新代入公式十七,得到:
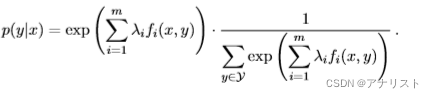 (公式二十)
(公式二十)
对上式简单改写,就得到著名的最大熵模型:
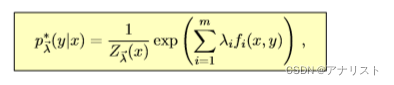 (公式二十一)
(公式二十一)
其中就是公式二十的分母,即:
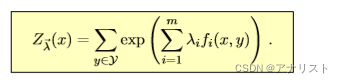 (公式二十二)
(公式二十二)
条件随机场(Conditional Random Fields)
条件随机场(即CRF)可看成最大熵模型的序列版本(sequence version),这意味着它们都是判别式模型。CRF与HMM对比,除了后者是生成式模型之外,二者另一个重要的不同点是,CRF不再局限于线性序列结构,而可以是任意结构,当然线性结构是最常见的。
CRF基本原则
CRF是一种计算的概率模型,其中输出向量
,对应的输入向量(也叫做观测值)
。要知道在无向图中,概率分布可以用称为最大团的非负函数的乘积表示,其中每个因子包含来自不同团的节点,这意味着条件独立的节点不会出现在同一个因子中,作为一种无向图,CRF推导的起点一般是以下公式:
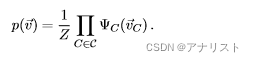 (式1)
(式1)
其中是CRF结构图中对应于不同最大团的因子,每个因子对应一个随机变量
的势函数,其中势函数一般由观测值的不同特征
组合而成。当然,势函数可以是任意的函数,甚至可以不必是概率函数,因此势函数乘积的归一化必不可少,这是为了保证最终得到有意义的概率值。这是通过归一化因子Z来实现的。Z的表达式为:
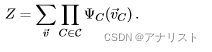 (式2)
(式2)
在参数学习(或模型训练)中对Z的计算是非常重要且具有挑战性的,因为这需要对所有可能的变量进行求和。需要指出,最大熵模型(公式二十一、二十二)也符合式1和式2,其中非负势函数取指数函数,而取观测值的不同特征
的加权求和。
CRF的条件概率可进行如下推导:
 (式3)
(式3)
其中第一步是贝叶斯公式;第二步把展开成对
求和的形式,故需引入变量
,从而变为联合概率
;第三步对分子和分母分别套用式1,其中随机变量
用输入变量
和输出变量
分开表示。
当然也可以直接把式1表示成如下形式:
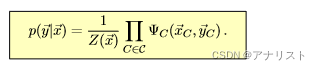 (式4)
(式4)
其中归一化因子的表达式可参考式3的第三步的分母,为:
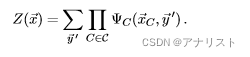 (式5)
(式5)
注意:到目前为止都是CRF的通用形式,而不只表示线性结构。
线性链CRF(Linear-chain CRFs)
作为CRF的特例,线性链CRF把输出变量建模成序列数据,我们把式4写成如下形式:
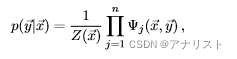 (式6)
(式6)
其中也作相应调整:
 (式7)
(式7)
我们假设每个因子符合如下形式(和最大熵模型类似,但更为复杂):
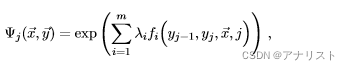 (式8)
(式8)
假设观测序列的长度为n+1,即有n+1个y节点,那么因子数就是n(因为相邻的两个位置变量和
被合并为一个因子),那么线性链CRF可重写为:
 (式9)
(式9)
上式通过结合式6和式8,把对指数函数的累乘改写成对其肩上数字的累加得到。与最大熵模型最大的区别是,式9比公式二十一多了一层对j的累加,这是因为CRF不再只是预测单标签,而是要预测标签序列。在式9中,j指定了输入序列的位置下标。而权重
完全不依赖位置下标j。
类似的,为了归一化条件概率到[0,1]区间,对应的分母为:
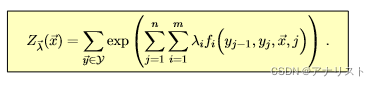 (式10)
(式10)
上式是对所有可能的标签序列求和,目的是最终得到可行的概率值。
对式9可以进行三种变形,分别是:
1) 将代表序列位置的j求和移动到exp前面,如下所示:
 (式11)
(式11)
2) 将代表不同特征的i求和移动到exp前面,如下所示:
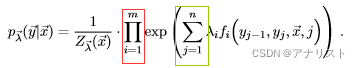 (式12)
(式12)
对于式12,因子不再在序列中流动构造,而是在特征中流动构造。
3) 同时将i和j的求和移动到exp前面,如下所示:
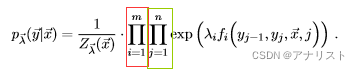 (式13)
(式13)
需要指出,式11的因子一般基于最大团,而式12和式13不需要满足这个要求。一般来说,因子化时如果不是用最大团,会导致某种程度的不准确,因为并不是所有的依赖都被正确考虑到,有时会导致冗余计算。后面会基于式11进行分析。
和HMM的三个基本问题相似,线性链CRF也有两个基本问题,分别是:
1. 给定观测值和CRF模型M,求最有可能的标签序列
2. 给定标签序列![]() ,和观测序列
,和观测序列,求CRF模型M的参数,使得
最大
其中问题1是CRF最常见的应用,而问题2是如何训练来调整模型参数,尤其是特征权重。注意:在判别式模型中,概率
不需要建模,而HMM中是需要的。
训练过程
在训练集上进行最大似然估计,目标函数
为:
 (式14)
(式14)
为了避免过拟合,一般要加上惩罚项,注意这个技术细节也能用在最大熵模型中。
推导过程如下:
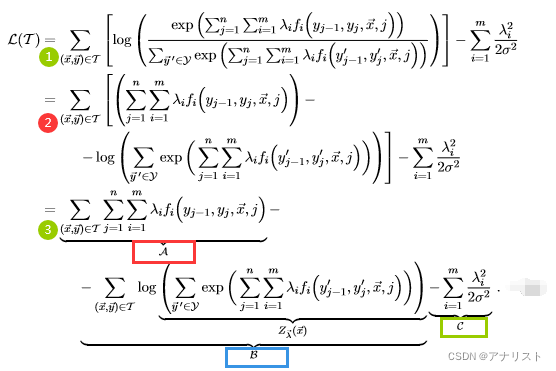 (式15)
(式15)
第1步对式14加上惩罚项;第2步将log的分子分母转化成相减的形式,并把第一项的log和exp抵消掉,但保留第二项;第3步将第一项不必要的括号省略,并记做A,将第二项记做B,其中log的内容记为,将第三项(即惩罚项)记做C。注意:A项、B项、C项都包含特征权重
!
A项、B项、C项对权重(或
)的偏导可以分开计算。其中A项的偏导计算很简单,如下:
 (式16)
(式16)
B项的偏导计算过程较为复杂,如下:
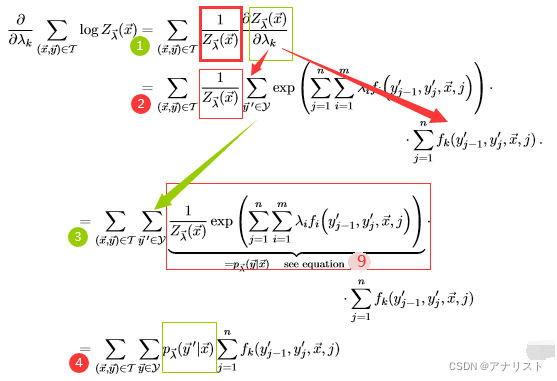 (式17)
(式17)
其中第一步是对求偏导,利用链式求导法则;第二步继续求
对
的偏导,利用链式求导法则,以及exp指数的导数是它自己;第三步将
移动到第二层
求和以内,并与exp项一起合并为
,具体见式9;第四步就是最终结果。
C项的偏导计算很简单,如下:
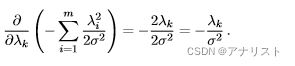 (式18)
(式18)
注意,式15所示的似然函数是凹函数,这是因为:第一项关于(或
)是线性的,见式16;第二项由于log是凹函数,而内部的
是线性的,不改变凹凸性,所以还是凹函数;第三项是开口向下的二次函数,也是凹函数;所以整体还是凹函数。
式16(A项的偏导)从含义上,其实就是特征的经验分布的期望值(可类比公式五),具体如下:
 (式19)
(式19)
式17(B项的偏导)从含义上是模型分布的期望值(可类比公式九),具体如下:
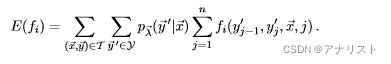 (式20)
(式20)
因此对权重
(或
)的偏导可看成:
![]() (式21)
(式21)
式19和式20分别与最大熵模型的公式五和公式九对应,其中最大区别是因子的消失,而这一点对于通过近似推导
找最大值是不相关的。需要注意:线性链CRF中直接计算
是不可行的,因为存在大量可能的序列标注;而在最大熵模型中这点是可行的,因为输出变量y的不同值比较少。CRF中输出序列存在巨大的组合复杂性,因此需要一个DP算法,也就是HMM中的前向-后向算法,只需要简单的修改即可。
首先定义一个函数用于将输入位置为j的单个状态s映射到位置为j+1的下一个状态的集合,再定义一个逆函数
将所有可能的下一个状态的集合映射回s。特殊状态
和
分别表示序列的开始和结束。前向和后向分别用
和
表示,可看成线性链CRF中的消息传递,递推公式如下:


和式8的势函数定义一致,特征被定义在特定状态(如和
)之上,例如:
![]()
函数将消息从链头传递到链尾,
相反。二者初始化如下:
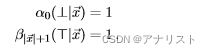
有了和
的初始值和递推关系,就能非常高效的计算模型分布的期望值
,具体如下:
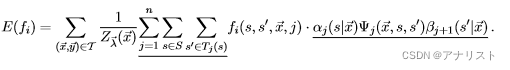 (式26)
(式26)
其中下划线部分可看成在计算状态序列的所有组合构成的势函数。一个可视化的网格图如下:
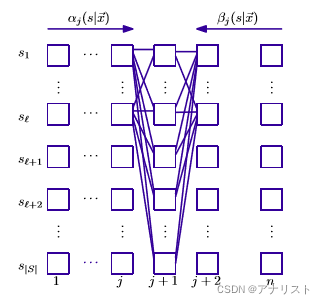 (图1)
(图1)
其中每一列表示一个序列位置j的多个状态s,每一行表示不同序列位置,所有可能的消息传递路径被描绘出来。每个和
一次迭代计算后被保存,因此只需要计算一次。归一化因子的公式为:
![]() (式27)
(式27)
前向-后向算法时间复杂度为,即与序列长度线性相关,而与状态数是二次相关。
推理过程
推理是为了找到给定观测序列对应的最有可能的状态序列
,与HMM的解码类似,这里不是为了找到每个单独最有可能的状态,而是为了最大化预测正确的状态数。所以这里同样要用维特比算法(Viterbi algorithm)。维特比算法和前向-后向算法类似,只不过将求和改为最大化。
定义一个函数表示在位置j以状态s结束的序列概率的最高分,即有:
![]() (式28)
(式28)
它的递推关系表示为:
![]() (式29)
(式29)
用函数用来跟踪j和s的值,整个算法流程如下:
1. 初始化。将起始状态到所有可能的第一个状态s的
函数值设为对应的
因子值,并将起始状态
保存到
函数中,具体如下:
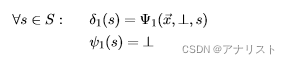 (式30)
(式30)
2. 迭代过程。下一步的值通过当前值计算得到,具体如下:
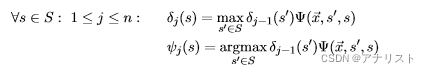 (式31)
(式31)
3. 终止结果:


4. 路径回溯,利用重新计算最优路径,找到状态序列:
![]() (式34)
(式34)
仔细观察,前3步非常像前向-后向算法。总的来说,维特比算法先在网格中填充最优值,然后第4步在网格中读取最优路径。
任意结构CRF(Arbitrarily structured CRFs)
任意结构CRF指的是树或者网格结构,从线性链结构CRF转到任意结构CRF需要丢掉一些团构建的约束条件,因此需要更通用的训练和推理算法。比如有文献提出了Skip Chain结构,如下图b:
 (图2)
(图2)
可以看到,b图和a图的区别是,相邻的位置可能没有连接,而不相邻的节点可能有连接,有点像深度学习的残差网络(也许比它更早出现)。
对于线性链CRF(图2a),它的势函数来自以下团模板(clique templates):
![]() (式35)
(式35)
这个单一的模板意味着,线性链CRF只能连接两个相邻的位置j和j-1.
对于跳跃链CRF(图2b),它的势函数来自两个团模板:
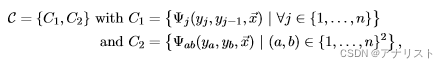 (式36)
(式36)
可以看到,C1模板和式35一样,而C2模板的两个节点和
可以不相邻,即它们都只要满足在全域范围内即可,当然也可以另外规定b是a的整数倍等等。注意:C1和C2模板是或的关系,即只需满足一个就要建立连接。比如,有5个节点的跳跃链CRF,输入序列
,根据C1模板,2和3、3和4、4和5、5和6都要建立连接,而根据C2模板(即b是a的整数倍),就有2和4、2和6、3和6建立连接,那么就得到如下结构图和因子图:
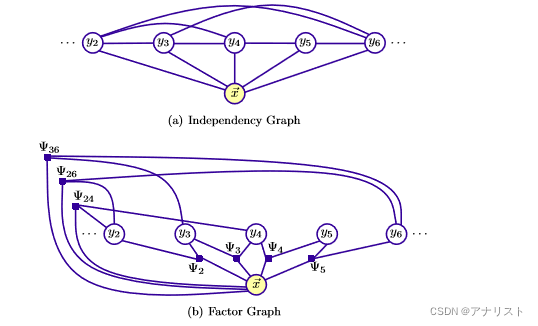 (图3)
(图3)
在训练和推理时,序列结构(无论HMM还是线性链CRF)都采用前向-后向算法和维特比算法,即通过往链上的两个方向发送消息来实现。而对于树结构的CRF甚至任意结构CRF,一般采用最大和(max-sum)算法和sum-product算法。具体见《PRML》的8.4节。
参考资料
《Classical Probabilistic Models and Conditional Random Fields》,2007 年。
《模式识别与机器学习》,2006 年。
《统计学习方法》,2012年。




















 6573
6573











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








