MATLAB得到贝塞尔函数零点

有时，我们需要求解贝塞尔函数的零点
MATLAB的数值求解函数fzero()可以用来解决这个问题：

clear
besselj1 = @(x)besselj(1,x) %一阶贝塞尔函数的匿名函数形式
for n = 1:10
    z(n) = fzero(besselj1,[(n-1) n]*pi);
end

x = 0:pi/100:10*pi;
y = besselj(1,x);
plot(z,zeros(1,10),'o',x,y,'-');
line([0 10*pi],[0 0],'color','black')
axis([0 10*pi -0.5 1.0])
xlabel('U')
ylabel('J_1(U)')

结果：

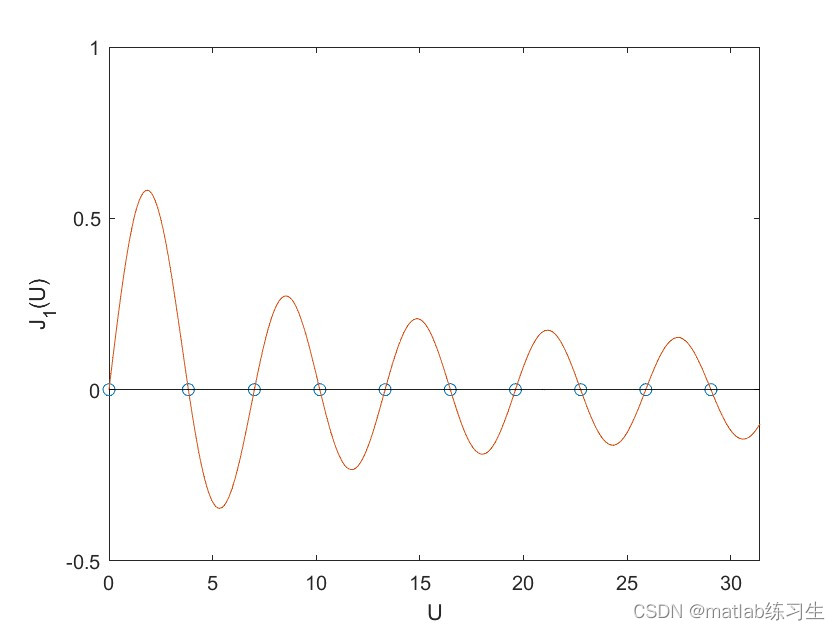
 图中贝塞尔函数的零点被圆圈标出，需要注意的是，这里对每一个零点做了一个划分，既假定零点在（n-1）*pi和n*pi之间。

这可以从贝塞尔函数的性质得到解释。

如果需要精确的数值，可以使用如下语句：

[(1:n)' z']

可以得到刚才求出的前十个数值解。

结果：

来源《高等光学仿真——光波导、激光》