【时间序列】选择最佳模型，ARIMA、SARIMA、指数平滑法、prophet！！

最新推荐文章于 2024-09-11 20:14:24 发布

风度78

最新推荐文章于 2024-09-11 20:14:24 发布

阅读量761

点赞数

原文链接：https://mp.weixin.qq.com/s?__biz=MzIwODI2NDkxNQ==&mid=2247520726&idx=2&sn=b0bd0e2242ddbd0b011515d0d4599165&chksm=964aa85eb805703b2af181cb3dad0f3e443580acc769e6f63991b79b3c196194a2458ee8efaf&scene=126&sessionid=0

版权

今儿给大家带来了关于时间序列模型，比较常见的四种算法对比。

时间序列算法模型用于分析和预测随时间变化的数据。主要模型有ARIMA、SARIMA、指数平滑法、prophet、深度学习模型（如LSTM）等等。

这些模型可以用来预测未来趋势、检测异常和分析数据中的周期性变化。

本期最佳模型

1. ARIMA

原理

ARIMA是一种常用的时间序列预测模型，综合了自回归（AR）、差分（I）和移动平均（MA）三个部分。ARIMA模型假设时间序列是非平稳的，通过差分使其平稳，然后使用AR和MA模型进行建模。

AR（自回归）： 使用过去的值预测未来值。
I（差分）： 消除时间序列中的趋势，使之平稳。
MA（移动平均）： 使用过去预测误差的线性组合来预测未来值。

核心公式

ARIMA模型的数学表示为：

：时间序列的当前值。
：常数项。
：自回归系数（AR部分）。
：移动平均系数（MA部分）。
：误差项。
：AR部分的阶数。
：MA部分的阶数。

差分运算：

差分的次数（即I部分的阶数）为d。

算法流程

1. 数据平稳化： 通过差分操作使时间序列平稳。

2. 选择模型阶数： 使用自相关函数（ACF）和偏自相关函数（PACF）确定p和q的值。

3. 模型拟合： 使用历史数据拟合ARIMA模型。

4. 预测： 利用拟合好的模型进行未来值的预测。

优缺点

优点：

对时间序列的趋势和季节性有较好的捕捉能力。
模型较为成熟，理论基础坚实。

缺点：

需要平稳时间序列，差分操作可能导致数据过度平稳化。
参数选择复杂（p, d, q）。
对于长期预测效果不佳。

适用场景

数据具有较强的趋势性或季节性。
需要短期的时间序列预测。

2. SARIMA

原理

SARIMA是ARIMA模型的扩展，专门用于处理具有季节性成分的时间序列。通过引入季节性自回归（SAR）、季节性差分（SI）和季节性移动平均（SMA）部分来建模季节性。

核心公式

SARIMA模型表示为：

：季节周期长度。
：季节性部分的AR, I, MA阶数。
其他符号与ARIMA模型相同。

算法流程

1. 数据平稳化： 包括常规差分和平稳化以及季节性差分。

2. 选择模型阶数： 使用ACF和PACF确定p、q、P、Q的值。

3. 模型拟合： 拟合SARIMA模型。

4. 预测： 基于模型进行预测。

优缺点

优点：

能处理复杂的季节性成分。
扩展了ARIMA模型的应用范围。

缺点：

模型复杂，参数更多，选择难度更大。
计算量较大。

适用场景

数据存在显著的季节性波动（如月度销售数据）。
需要预测带有季节性特征的时间序列。

3. 指数平滑法

原理

指数平滑法通过对历史数据进行加权平均，其中最近的数据被赋予更高的权重。它主要有三种形式：简单指数平滑、霍尔特线性趋势平滑（Holt’s Linear Trend Model）、霍尔特-温特斯季节性平滑（Holt-Winters Seasonal Model）。

核心公式

简单指数平滑（Simple Exponential Smoothing）：

：平滑系数，范围为0到1。
：下一时刻的预测值。
霍尔特线性趋势（Holt’s Linear Trend）：
霍尔特-温特斯季节性（Holt-Winters Seasonal）： 加入了季节性成分，可以是加法模型或乘法模型。

算法流程

1. 选择平滑系数（等）： 根据数据特点和实验结果选择。

2. 更新平滑值： 依次更新平滑值、趋势、季节性。

3. 预测未来值： 基于平滑后的值进行预测。

优缺点

优点：

模型简单，容易实现。
对短期预测效果好。

缺点：

对长期预测效果差。
参数选择对预测结果影响较大。

适用场景

数据没有明显的季节性，但可能存在趋势。
适合短期预测，适用于库存控制、需求预测等。

4. prophet

原理

prophet 是由Facebook开发的时间序列预测工具，专为处理具有强季节性和假期效应的数据而设计。它通过将时间序列分解为趋势、季节性和假期效应三个部分来建模，并使用可加性模型进行预测。

核心公式

Prophet模型的核心公式是：

：趋势函数（线性或逻辑回归）。
：季节性成分，通常是年周期。
：假期效应（对特定日期的修正）。
：误差项。

趋势函数：

线性趋势：
饱和增长：

算法流程

1. 模型分解： 将时间序列分解为趋势、季节性和假期效应。

2. 模型拟合： 使用分段线性或逻辑回归拟合趋势部分，使用傅里叶级数拟合季节性部分，处理假期效应。

3. 预测： 将各部分预测结果叠加得到最终预测值。

优缺点

优点：

处理季节性和假期效应特别方便。
可视化好，参数易于调节。
适合非技术人员使用。

缺点：

对非季节性数据效果一般。
对长时间跨度的数据可能过拟合。

适用场景

数据具有显著的季节性或节假日效应。
需要快速上手并获得较好的预测结果。
电商销量预测、网络流量预测等。

代表案例

下面，是使用 ARIMA、SARIMA、指数平滑法（ETS）和 Prophet 进行时间序列预测的综合案例。

在这个案例中，我们使用一个虚拟的数据集，并且使用这四种方法进行预测。

最后绘制三个不同形式的图表来比较这些算法的预测结果，并详细讨论它们的适用性、性能以及调参细节。

数据生成

我们生成一个包含趋势、季节性和噪声的虚拟时间序列数据。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 设置随机种子以确保可重复性
np.random.seed(42)

# 生成日期范围
dates = pd.date_range(start='2020-01-01', periods=100, freq='M')

# 生成趋势、季节性和噪声
trend = np.linspace(10, 50, 100)
seasonality = 10 * np.sin(np.linspace(0, 3 * np.pi, 100))
noise = np.random.normal(scale=5, size=100)

# 创建数据集
data = trend + seasonality + noise
df = pd.DataFrame({'Date': dates, 'Value': data})
df.set_index('Date', inplace=True)

# 可视化生成的数据
plt.figure(figsize=(10, 6))
plt.plot(df.index, df['Value'], label='Generated Data', color='blue')
plt.title('Generated Time Series Data')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()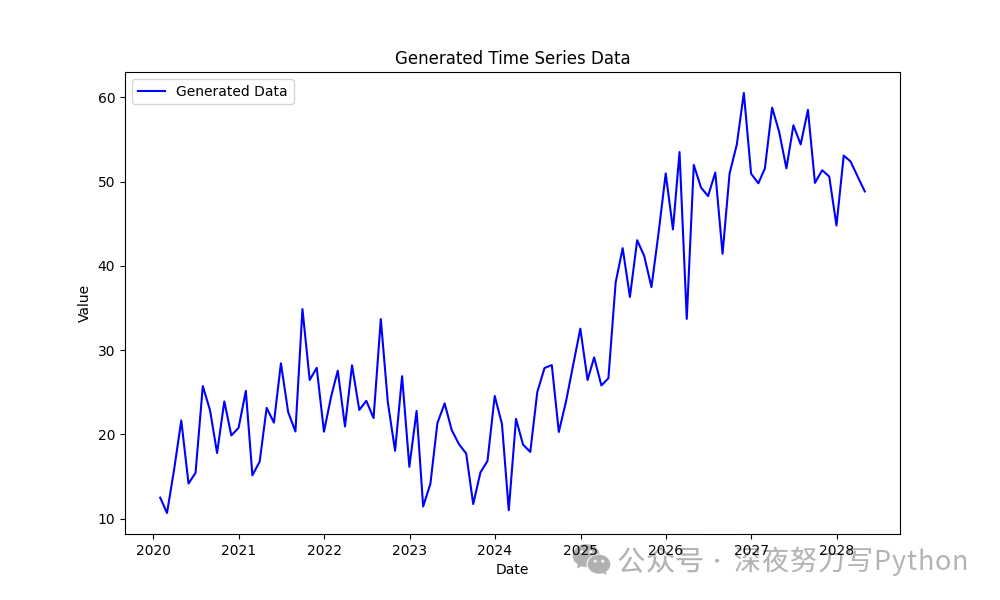

ARIMA 模型

ARIMA 适用于无季节性的时间序列数据。我们将对数据进行建模，并进行预测。

from statsmodels.tsa.arima.model import ARIMA

# 拟合 ARIMA 模型
arima_model = ARIMA(df['Value'], order=(5, 1, 0))
arima_result = arima_model.fit()

# 预测
df['ARIMA_Prediction'] = arima_result.predict(start=1, end=len(df), dynamic=False)

# 可视化 ARIMA 预测结果
plt.figure(figsize=(10, 6))
plt.plot(df.index, df['Value'], label='Actual', color='blue')
plt.plot(df.index, df['ARIMA_Prediction'], label='ARIMA Prediction', color='red')
plt.title('ARIMA Model Prediction')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()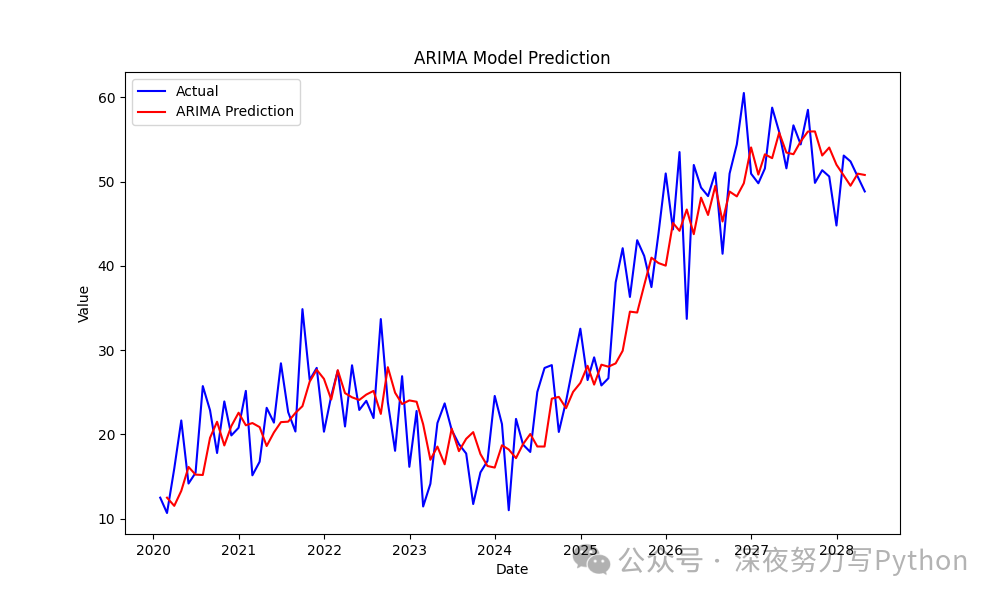

SARIMA 模型

SARIMA 是 ARIMA 的扩展，适用于带有季节性的时间序列数据。

from statsmodels.tsa.statespace.sarimax import SARIMAX

# 拟合 SARIMA 模型
sarima_model = SARIMAX(df['Value'], order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
sarima_result = sarima_model.fit()

# 预测
df['SARIMA_Prediction'] = sarima_result.predict(start=1, end=len(df), dynamic=False)

# 可视化 SARIMA 预测结果
plt.figure(figsize=(10, 6))
plt.plot(df.index, df['Value'], label='Actual', color='blue')
plt.plot(df.index, df['SARIMA_Prediction'], label='SARIMA Prediction', color='green')
plt.title('SARIMA Model Prediction')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()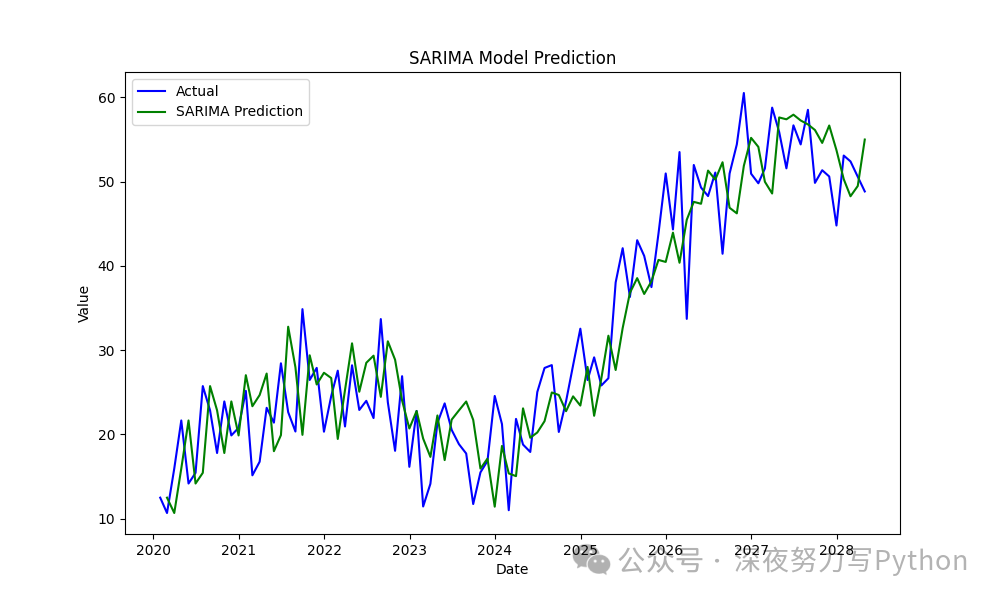

指数平滑法 (ETS)

ETS 模型适用于具有趋势和季节性的时间序列数据。

from statsmodels.tsa.holtwinters import ExponentialSmoothing

# 拟合 ETS 模型
ets_model = ExponentialSmoothing(df['Value'], trend='add', seasonal='add', seasonal_periods=12)
ets_result = ets_model.fit()

# 预测
df['ETS_Prediction'] = ets_result.predict(start=1, end=len(df))

# 可视化 ETS 预测结果
plt.figure(figsize=(10, 6))
plt.plot(df.index, df['Value'], label='Actual', color='blue')
plt.plot(df.index, df['ETS_Prediction'], label='ETS Prediction', color='purple')
plt.title('ETS Model Prediction')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()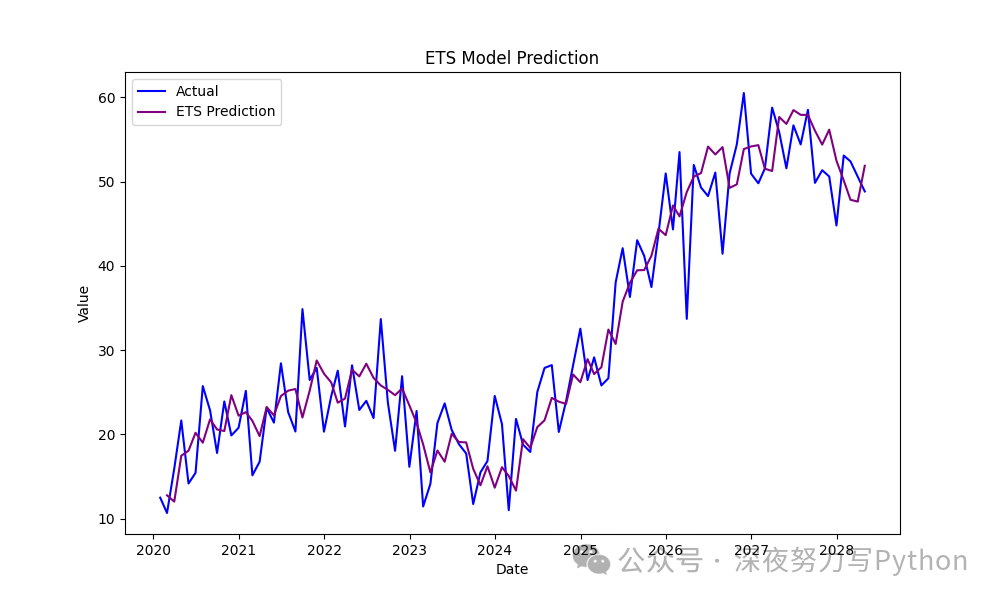

Prophet 模型

Prophet 适用于具有复杂趋势和季节性的时间序列数据，并且在处理缺失值和异常值时表现良好。

from prophet import Prophet

# Prophet 需要特定的数据格式
df_prophet = df.reset_index().rename(columns={'Date': 'ds', 'Value': 'y'})

# 拟合 Prophet 模型
prophet_model = Prophet(yearly_seasonality=True, weekly_seasonality=False, daily_seasonality=False)
prophet_model.fit(df_prophet)

# 预测
future = prophet_model.make_future_dataframe(periods=0)
forecast = prophet_model.predict(future)

# Prophet 结果处理
df['Prophet_Prediction'] = forecast['yhat'].values

# 可视化 Prophet 预测结果
plt.figure(figsize=(10, 6))
plt.plot(df.index, df['Value'], label='Actual', color='blue')
plt.plot(df.index, df['Prophet_Prediction'], label='Prophet Prediction', color='orange')
plt.title('Prophet Model Prediction')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()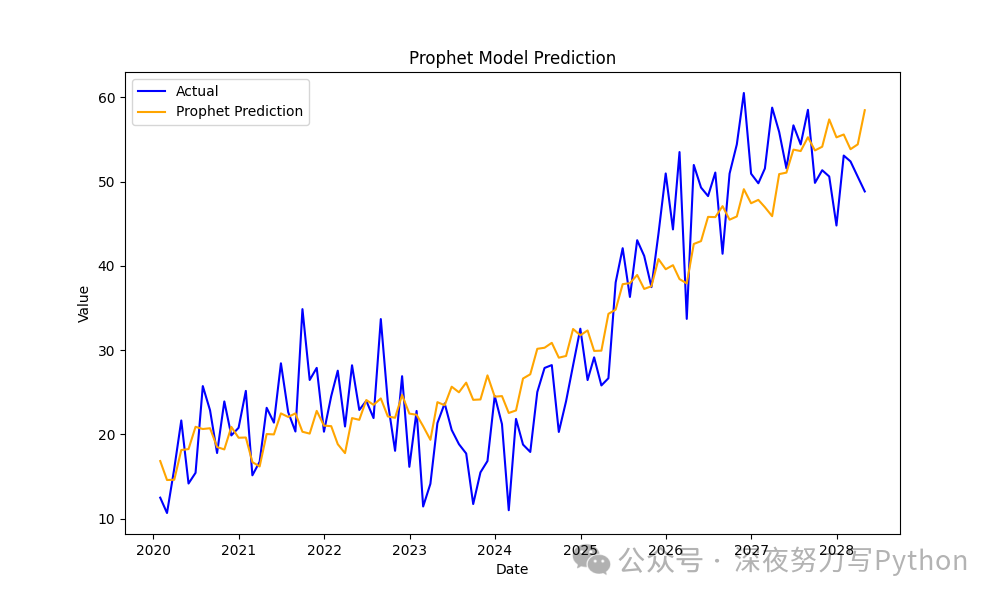

综合对比分析

将所有模型的预测结果绘制在一起进行比较。

plt.figure(figsize=(14, 8))
plt.plot(df.index, df['Value'], label='Actual', color='black', linewidth=2)
plt.plot(df.index, df['ARIMA_Prediction'], label='ARIMA Prediction', color='red')
plt.plot(df.index, df['SARIMA_Prediction'], label='SARIMA Prediction', color='green')
plt.plot(df.index, df['ETS_Prediction'], label='ETS Prediction', color='purple')
plt.plot(df.index, df['Prophet_Prediction'], label='Prophet Prediction', color='orange')
plt.title('Comparison of Different Time Series Models')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()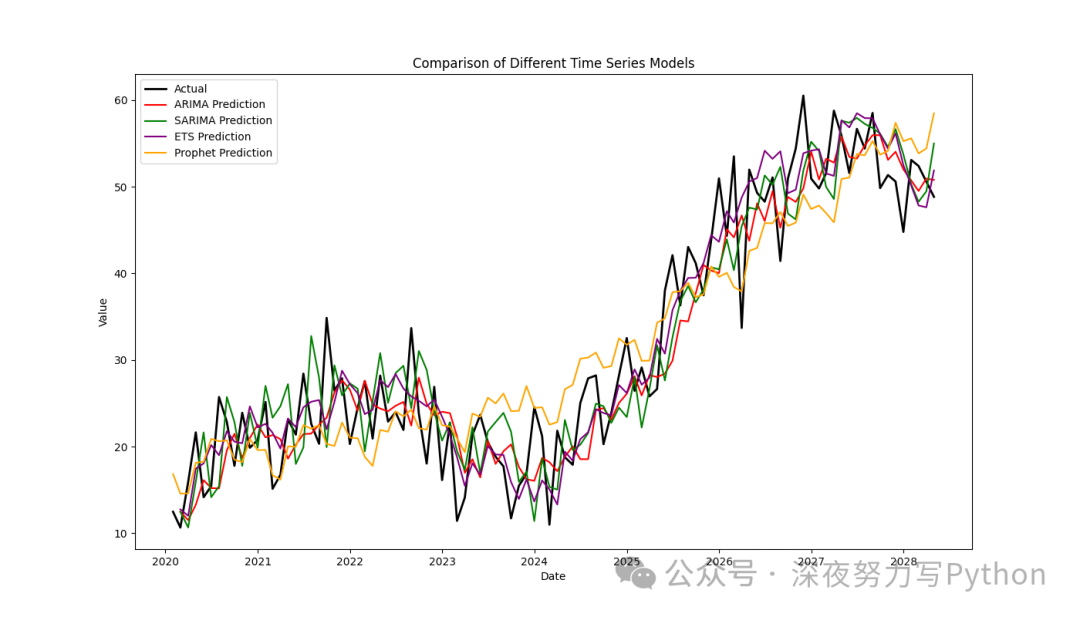

不同形式的数据分析绘图

「残差分析图」

我们可以绘制每个模型的残差图，以观察预测误差的分布。

plt.figure(figsize=(14, 8))

plt.subplot(2, 2, 1)
plt.plot(df.index, df['Value'] - df['ARIMA_Prediction'], color='red')
plt.title('ARIMA Residuals')

plt.subplot(2, 2, 2)
plt.plot(df.index, df['Value'] - df['SARIMA_Prediction'], color='green')
plt.title('SARIMA Residuals')

plt.subplot(2, 2, 3)
plt.plot(df.index, df['Value'] - df['ETS_Prediction'], color='purple')
plt.title('ETS Residuals')

plt.subplot(2, 2, 4)
plt.plot(df.index, df['Value'] - df['Prophet_Prediction'], color='orange')
plt.title('Prophet Residuals')

plt.tight_layout()
plt.show()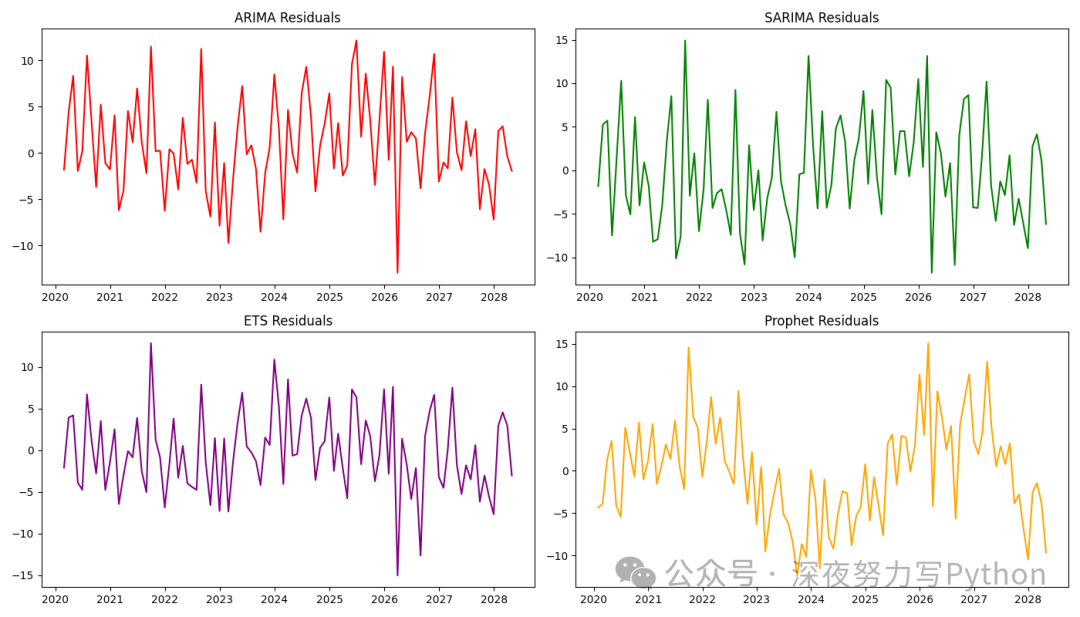

「预测误差的分布直方图」

绘制每个模型的预测误差的分布直方图，了解误差的分布情况。

plt.figure(figsize=(14, 8))

plt.subplot(2, 2, 1)
plt.hist(df['Value'] - df['ARIMA_Prediction'], bins=20, color='red', alpha=0.7)
plt.title('ARIMA Prediction Error Distribution')

plt.subplot(2, 2, 2)
plt.hist(df['Value'] - df['SARIMA_Prediction'], bins=20, color='green', alpha=0.7)
plt.title('SARIMA Prediction Error Distribution')

plt.subplot(2, 2, 3)
plt.hist(df['Value'] - df['ETS_Prediction'], bins=20, color='purple', alpha=0.7)
plt.title('ETS Prediction Error Distribution')

plt.subplot(2, 2, 4)
plt.hist(df['Value'] - df['Prophet_Prediction'], bins=20, color='orange', alpha=0.7)
plt.title('Prophet Prediction Error Distribution')

plt.tight_layout()
plt.show()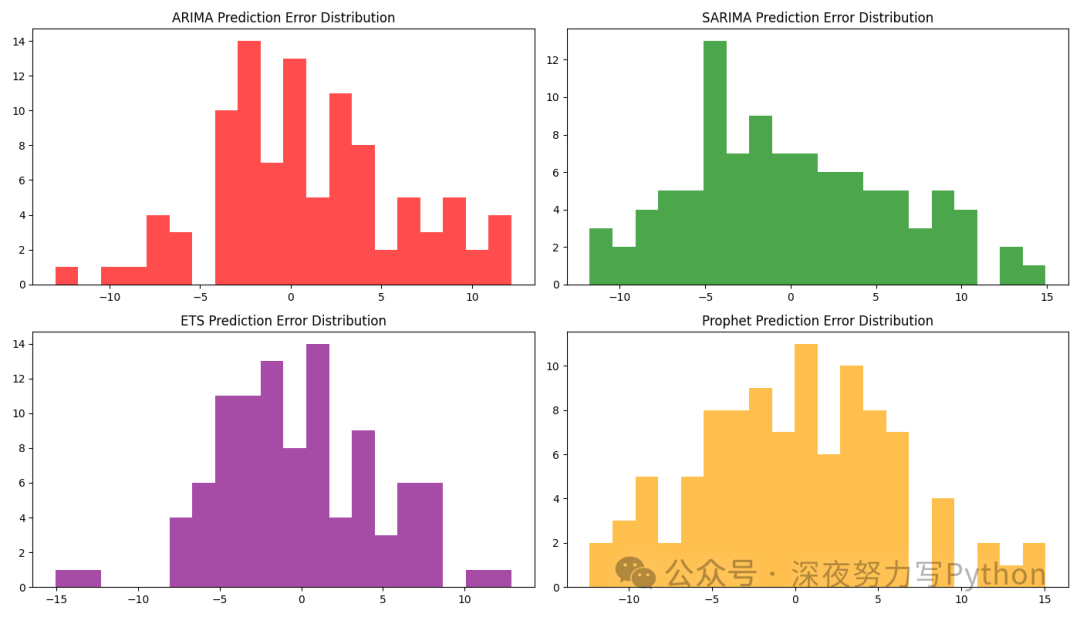

「模型预测与实际值的相对误差」

绘制每个模型预测值与实际值的相对误差百分比，以更直观地比较模型的预测准确性。

plt.figure(figsize=(14, 8))

plt.subplot(2, 2, 1)
plt.plot(df.index, (df['Value'] - df['ARIMA_Prediction']) / df['Value'] * 100, color='red')
plt.title('ARIMA Relative Error (%)')

plt.subplot(2, 2, 2)
plt.plot(df.index, (df['Value'] - df['SARIMA_Prediction']) / df['Value'] * 100, color='green')
plt.title('SARIMA Relative Error (%)')

plt.subplot(2, 2, 

3)
plt.plot(df.index, (df['Value'] - df['ETS_Prediction']) / df['Value'] * 100, color='purple')
plt.title('ETS Relative Error (%)')

plt.subplot(2, 2, 4)
plt.plot(df.index, (df['Value'] - df['Prophet_Prediction']) / df['Value'] * 100, color='orange')
plt.title('Prophet Relative Error (%)')

plt.tight_layout()
plt.show()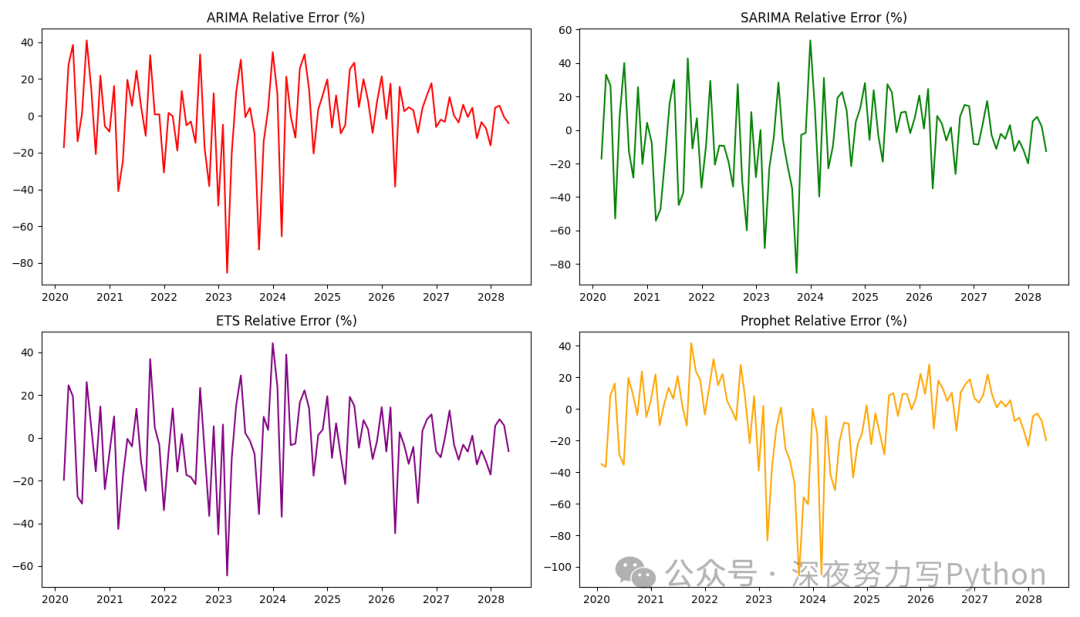

适用性和性能比较

ARIMA: 适用于无季节性或季节性非常微弱的时间序列。数据中存在明显季节性时效果较差。
SARIMA: 在数据具有季节性模式时表现良好，适合捕捉季节性和非季节性成分。
ETS (指数平滑法): 适用于具有趋势和季节性的时间序列，在处理复杂的趋势和季节性变化时表现良好。
Prophet: 适用于具有复杂趋势和多种季节性的时间序列，处理缺失值和突变时表现优异。

调参细节

ARIMA: 通过调整 p、d、q 参数来平衡模型的复杂度和预测性能。通常使用 AIC 或 BIC 选择最优参数。
SARIMA: 需要调整季节性参数 P、D、Q 和季节周期 m。与 ARIMA 相似，可以通过网格搜索或自动化工具来选择最优参数。
ETS: 主要调节趋势 (additive/multiplicative) 和季节性模型类型。通过调节 seasonal_periods 参数匹配数据的周期性。
Prophet: 通过调整 changepoint_prior_scale 来控制趋势的灵活性。可以根据需要开启或关闭年、月、周等周期性成分。

最后

在不同的时间序列预测任务中，根据数据的特性选择合适的模型至关重要。通过这四种算法的对比，我们可以更清晰地理解各自的优缺点，并根据数据特性和任务需求进行选择和调参，从而实现更好的预测效果。

大家有问题可以直接在评论区留言即可~

往期精彩回顾




适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑

```
交流群
```

欢迎加入机器学习爱好者微信群一起和同行交流，目前有机器学习交流群、博士群、博士申报交流、CV、NLP等微信群，请扫描下面的微信号加群，备注：”昵称-学校/公司-研究方向“，例如：”张小明-浙大-CV“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~（也可以加入机器学习交流qq群772479961）