【深度学习】TPAMI 2024.9 | AdamW为什么比其他优化器具有更小的泛化误差

论文标题：Towards Understanding Convergence and Generalization of AdamW

论文翻译：关于理解 AdamW 的收敛性和泛化能力

论文链接：https://ieeexplore.ieee.org/document/10480574

论文作者：Pan Zhou; Xingyu Xie;Zhouchen Lin;Shuicheng Yan

---

摘要

AdamW 通过添加解耦的权重衰减来修改 Adam，以在每次训练迭代中减少网络权重。对于自适应算法，这种解耦的权重衰减不会影响特定的优化步骤，且不同于广泛使用的 L2 正则化器，后者通过改变一阶和二阶梯度矩来改变优化步骤。尽管 AdamW 在实践中取得了巨大成功，但关于 AdamW 相较于 Adam 和 L2 正则化的 Adam（L2-Adam）的收敛性和泛化能力提升仍未得到研究。为了解决这一问题，我们证明了 AdamW 的收敛性，并阐明了其相较于 Adam 和 L2-Adam 的泛化优势。具体来说，AdamW 可以证明是收敛的，但它最小化的是一个动态正则化损失，该损失结合了原始损失和由解耦权重衰减引发的动态正则化，因此表现出与 Adam 和 L2-Adam 不同的行为。此外，在一般的非凸问题和 PŁ 条件问题上，我们建立了 AdamW 的随机梯度复杂性，以找到一个稳定点。该复杂性同样适用于 Adam 和 L2-Adam，并改进了它们已知的复杂性，特别是在过度参数化的网络中。此外，我们证明了 AdamW 从贝叶斯后验角度来看，具有比 Adam 和 L2-Adam 更小的泛化误差。这个结果首次明确揭示了 AdamW 中解耦权重衰减的优势。实验结果验证了我们的理论。

关键词——自适应梯度算法、AdamW 分析、AdamW 收敛性、AdamW 泛化能力。

I.引言

自适应梯度算法，如 Adam [1]，由于其相较于随机梯度下降（SGD）[2] 具有更快的收敛速度，已经成为训练深度网络最流行的优化器，在计算机视觉 [3]、[4] 和自然语言处理 [5] 等领域中有许多成功的应用。与二阶算法中的预条件 [6] 类似，自适应算法根据损失目标的曲率调整每个梯度坐标的学习率。这种预处理通常帮助自适应算法比其非自适应算法（例如使用单一学习率的SGD）实现更快的收敛速度。不幸的是，这种预处理也带来了负面影响，即自适应算法通常在泛化性能上表现得比SGD更差[7] [8] [9]。

作为一种领先的自适应梯度方法，AdamW[11]显著提高了自适应算法在视觉Transformer (ViTs) 和卷积神经网络 (CNNs) 上的泛化性能。AdamW 的核心是解耦的权重衰减。具体来说，AdamW 像 Adam 一样使用指数移动平均来估计一阶矩 和二阶矩 ，然后使用学习率 、权重衰减参数 λ 和一个小常数 更新网络权重。可以观察到，AdamW 将权重衰减从相对于损失函数的优化步骤中解耦开来，因为无论损失和优化步骤是什么，权重衰减始终是 。这种解耦的权重衰减在 SGD 中成为 L2 正则化，但在自适应算法中有所不同。由于其有效性，AdamW 被广泛用于网络训练。然而，关于 AdamW 仍存在许多未解之谜。首先，尚不清楚 AdamW 是否能够理论上收敛，以及如果可以，能够达到何种收敛速度。此外，虽然 AdamW 在泛化性能上优于广泛使用的 Adam 和 L2 正则化的 Adam (L2-Adam)，但其理论原因很少被探讨，尽管这方面的研究需求很高。

接下来，我们从贝叶斯后验的角度理论证明了 AdamW 中解耦的权重衰减对泛化性能的好处。具体来说，我们证明了一个适当的解耦权重衰减 可以帮助 AdamW 实现较小的泛化误差，表明 AdamW 优于对应于 λ 的普通 Adam。我们进一步分析了 L2 正则化的 Adam，并观察到 AdamW 通常享有比 L2 正则化的 Adam 更小的泛化误差界。据我们所知，这项工作是首次明确显示 AdamW 优于 Adam 及其 L2 正则化版本的研究。

II.相关工作

收敛性分析：自适应梯度算法（如 Adam）由于其快速的收敛速度，已成为深度学习中的默认优化器。因此，许多研究探讨其收敛性以加深理解。在凸优化问题中，Adam 类型的算法（如 Adam 和 AMSGrad[19]）在线学习设置下具有 的遗憾（regret），其中 T 是训练迭代次数。在非凸问题中，Adam 类型的算法具有 的随机梯度复杂度，可以找到 ε-精确的驻点。RMSProp 和 Padam[17] 的复杂度为[16]，而 Adabelief[21] 的复杂度为 ，其中 c2 是随机梯度的 L2 范数上界。然而，尽管 AdamW 是视觉Transformer 和 CNN 的主要优化器，其收敛行为仍然不明确。

泛化性分析：大多数研究通过分析算法的随机微分方程（SDE）来研究算法的泛化性能，因为算法和其 SDE 的收敛行为相似。例如，通过将 SGD 公式化为布朗运动或莱维驱动的 SDE，SGD 被证明趋向于收敛到平坦的极小值，从而具有良好的泛化性。最近的研究表明，对于带有正则化层（如 BatchNormalization）的网络，权重衰减通过减小网络权重的规模来增加有效学习率，较高的学习率带来更大的梯度噪声，梯度噪声往往作为一种随机正则化手段。然而，Zhou 等人论证了权重衰减对没有正则化层（如全连接网络）的好处，并进一步实验证明了权重衰减对网络最后一层全连接层的正则化效果。不幸的是，现有研究并未明确展示 AdamW 中权重衰减对泛化性能的好处。我们借助上述的 SDE 工具和 PAC Bayesian 框架，明确分析了 AdamW 中解耦的权重衰减的泛化效应及其相较于 L2-Adam 的优越性。

III. 符号和预备知识

AdamW 和 L2-Adam：我们首先简要回顾 AdamW、Adam 和 L2-Adam 解决随机非凸问题的步骤：

其中损失函数f是可谓且非凸的，样本从分布D中抽取。为了解决上述问题，在第k次迭代中，AdamW估计当前梯度为小批量梯度，并使用三个常数、和更新变量：

这里，，所有涉及向量的操作（例如乘法、除法）都是逐元素的。这里允许 随着迭代次数 k 变化，因为在实际应用中，变化的 通常比固定的 展示更好的性能。有关 AdamW 的详细信息，请参见附录 B 的算法 1，在线提供。AdamW 在上述方程的第三步与普通的 Adam 不同。具体来说，AdamW 将权重衰减与优化步骤解耦，因为无论损失和优化步骤如何，权重衰减始终为 ηλ。而 L2-Adam 在梯度估计中添加了常规的权重衰减 λ，计算方式为 ，然后更新 和 （见2），并使用 。在许多网络中，AdamW 的解耦权重衰减通常比 L2-Adam 实现更好的泛化性能。

分析假设：在此我们介绍分析所需的假设，这些假设在文献 [1]、[8]、[19]、[34]、[35]、[36] 中常被使用。

**假设 1 (L-光滑性)**：如果存在 L>0，对所有 和 ，我们有 , 则函数 对参数是 L-光滑的。

**假设 2 (梯度假设)**：梯度估计 是无偏的，其幅度和方差有界：

当一个非凸问题满足假设 1 和 2 时，找到一个 ϵ-精确的一阶驻点的随机梯度复杂度下界（也称为 IFO 复杂度）为 [15]。接下来，我们介绍 Polyak-Łojasiewicz (PŁ) 条件，这在深度网络分析中被广泛使用，因为在 [37]、[38]、[39]、[40] 中观察或证明，深度神经网络在局部最小值附近通常满足 PŁ 条件。

**假设 3 (PŁ 条件)**：设 。如果函数 F(x)满足Ł 条件，即 其中 μ 是一个常数，则我们称函数 F(x) 满足 μ-PŁ 条件。

IV. 收敛性分析

在这里，我们首先使用一个具体的最小二乘问题来比较 AdamW 和 L2-Adam 的收敛行为。接下来，我们研究 AdamW 在一般非凸问题上的收敛性，并展示其在 PŁ 条件问题上的性能改进。

A. 特定最小二乘问题的结果

在这里，我们首先使用一个具体的最小二乘问题 (3) 来分析 AdamW 和 L2-Adam 的不同收敛性能：

其中 a 是一个不为零的常数。关于此问题的证明可以在附录 G.1 中找到，在线提供。

定理 1：假设随机梯度 是无偏的，满足 ，且 。那么，当学习率 和权重衰减 时，AdamW 生成的序列 满足：

其中 ，。当学习率 和 时，L2-Adam 生成的序列 满足：

在本章中，作者首先使用一个特定的最小二乘问题来比较AdamW和L2-Adam的收敛行为。接着，他们研究了AdamW在一般非凸问题上的收敛性，并展示了其在PŁ条件问题上的性能改进。

以下是文档中第4章B节“非凸问题的结果”的Markdown格式翻译：

B. 非凸问题的结果

现在我们讨论一般的非凸问题以及在Polyak-Łojasiewicz (PŁ) 条件下的问题。首先，我们在第 k 次迭代时定义一个动态替代函数 ，它实际上是原始损失函数 （来自方程(1)）与动态正则化项 的组合：

其中 ，并且 表示元素逐个相乘的内积。为了最小化方程(4)，可以通过泰勒展开近似原始损失函数 F(x)，并计算出 ：

因此得到：

考虑到在实践中 非常小，，并且与 相比，项 对于 来说很小，可以忽略不计。最终在随机设置中，可以使用梯度估计 来估算全梯度 ，因此得到的 更新公式为：

这与AdamW的更新步骤(2)一致。从这个过程可以看到，AdamW中的去耦权重衰减 诱导了动态正则化项 。接下来，我们将证明AdamW实际上是最小化动态函数 ，而不是原始损失 。

C. 一般非凸问题的结果

根据许多分析自适应梯度算法的研究【16, 18, 21, 41, 42】，我们首先通过使用恒定的学习率 提供 AdamW 的收敛结果。

定理 2：假设假设1和假设2成立。设 ，定义 ，且令 、和 在所有迭代中有效，权重衰减 为常数 。

在经过 次迭代后，AdamW 的更新序列 满足以下条件：

此外，实现这些条件所需的随机梯度复杂度为：

其证明详见在线附录G.2。定理2显示了 AdamW 在非凸问题上的收敛性。在 次迭代后，AdamW 的平均梯度

小于 ，表明了 AdamW 的收敛性。现在我们通过推论1展示小的 可以保证小的 ，其证明详见在线附录G.3。

推论1：假设 ，且常数，并且，我们有：

推论1中的假设是温和的。由于 是随机梯度 的移动平均值，特别是在训练的后期阶段，参数 的更新非常缓慢。因此可以假设，这在 Adam 分析工作中得到了验证，例如文献【9】。此外，假设 非常小，在实践中 ，因此可以找到常数 ，使得 $ || v_k ||_2 \leq || \nabla F(x_k) ||2 。对于假设 1 > \lambda_k \rho' | x_k |\infty $，它也是温和的，因为：

a) 实际上，权重衰减 通常非常小，例如 ，

b) 网络参数的最大范数 $ | x_k |\infty 并不大，这在文献【】中得到了证明，因为网络中不同层的参数大小之间存在自动适应的权衡。事实上，我们在训练良好的中观察到 | x_k |\infty \approx 8.0 $。

式(5) 中的第二个不等式保证了相邻解 和 之间的距离较小，这也显示了 AdamW 的良好收敛行为。最后一个不等式显示，历史随机梯度的指数移动平均 (EMA) 与全梯度 非常接近，这解释了 EMA 梯度估计的成功。

此外，在定理2中，为了找到 -精确的一级平稳点 (ASP)，AdamW 的随机梯度复杂度为 ，这与文献【15】中的下界 相匹配（仅差常数因子）。此外，AdamW 的复杂度比 Adabelief【21】的 和 LAMB【44】的 更低，特别是在过参数化的网络上， 限定了随机梯度的 范数上界。这是因为对于 d 维梯度，其 -范数 通常远小于其 -范数 ，并且在最佳情况下可以小 。

Appendix D 在线讨论了我们和上述工作的证明技术差异。可以将定理2中的结果扩展到 -Adam，参见附录 G.4 中的推论2。

推论2：在定理2中的相同参数设置下，Adam 和 -Adam 的随机梯度复杂度为 。

推论2 表明，Adam 和 -Adam 的复杂度为 ，并且优于之前已知的 Adam 类型优化器的复杂度 【16, 17, 18】，例如 -Adam、AdaGrad【34】、AdaBound【8】。虽然 AdamW 与 Adam 和 -Adam 共享相同的复杂度，但 AdamW 通过解耦的权重衰减将 -正则化器与损失目标分离，其泛化优势已在许多工作中得到了验证【12】，并在我们的第V节理论上得到了验证。

D. 针对 PŁ 条件的非凸问题的结果

在本研究中，我们特别关注满足 PŁ 条件的非凸问题，因为如 [37]，[38] 所观察到或证明的那样，深度学习模型通常至少在局部最小值附近满足 PŁ 条件。对于这种特殊的非凸问题，我们遵循 [18] 的做法，将整个优化过程分为 K 个阶段。具体来说，对于常数学习率设定，AdamW 在第 k 阶段使用学习率 ；对于衰减学习率设定，AdamW 在第 k 阶段使用衰减的 ，其满足 如果 ，其中 表示第 k 阶段第 i 次迭代的学习率。此外，对于两种学习率设定，AdamW 在第 k 阶段运行 次迭代，以实现 ，其中 ，是第 k 阶段的输出，表示优化精度。详细的算法 2 请参见附录 B，在线可用。以下我们分别给出了常数和衰减学习率设定下 AdamW 的收敛结果，详细见定理 4，证明在附录 G.6，在线可用。

定理 4：假设满足假设 1 和 2，且 。假设损失函数 和 满足假设 3 中的 PŁ 条件。

1. 对于常数学习率设定，假设常数学习率 ，常数 ，并且 在第 k 阶段。我们有：

1.1) 对于第 k 阶段，AdamW 至多运行 次迭代以实现 ，其中输出 是第 k 阶段的序列 中的随机选择。

1.2) 对于 K 个阶段，总的随机复杂度为 以实现 。

1. 对于衰减学习率设定，设 ，，，在第 k 阶段的第 i 次迭代中，其中 。

2.1) 对于第 k 阶段，AdamW 至多运行 次迭代以实现 ，其中输出 是根据分布 从序列 中随机选择的。

2.2) 总的复杂度为 以实现 。

定理 4 说明了 AdamW 在常数和衰减学习率设定下均可收敛。此外，通过对比，要实现 (6) 中的 -准确度点，衰减学习率的总复杂度为 ，并且可能比常数学习率的复杂度 更好。

V. 泛化性分析

本节内容主要聚焦于AdamW优化算法的泛化性能与收敛性分析，提出了其相对于传统Adam和L2正则化Adam的显著优势，并通过理论和实验验证加以支持。

泛化性能分析

AdamW通过引入去耦合的权重衰减，使其与传统的L2正则化方法不同。传统的L2正则化会直接影响优化步骤，而AdamW的去耦合机制使得权重衰减与优化步骤分离，从而能够更好地控制模型的泛化能力。基于PAC-Bayesian框架，作者对AdamW的泛化误差上界进行了推导，证明了在适当的权重衰减参数下，AdamW能够实现比L2正则化Adam更小的泛化误差。这个结果表明，AdamW在处理泛化问题上具有显著的理论优势。

泛化误差推导

通过对算法的随机微分方程（SDEs）的分析，作者探讨了AdamW的后验假设及其泛化行为。具体而言，AdamW的更新规则可以被描述为：

其中，是梯度噪声，是对角矩阵，描述了梯度的自适应调整。进一步假设梯度噪声服从高斯分布，作者将AdamW的更新过程转化为随机微分方程（SDE），并推导出其泛化误差的理论表达式。这一过程揭示了AdamW的去耦合权重衰减如何通过降低噪声，从而提升模型的泛化能力。

VI 实验

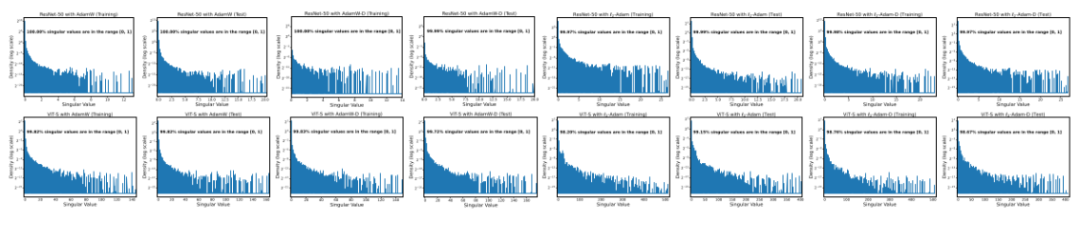
关于Hessian矩阵奇异值的研究：我们分别使用AdamW和L2正则化Adam（L2-Adam）在ImageNet数据集上训练了ResNet50和ViT-small这两种流行的网络。AdamW和L2-Adam都使用了恒定的权重衰减参数 ，而AdamW-D和L2-Adam-D则使用了指数衰减的权重衰减参数 （其中 且 ）。图1展示了在ImageNet上的训练和测试数据中的这些奇异值的谱密度，显示超过99%的奇异值在[0,1]范围内且远小于1。这与AlexNet、VGG和ResNet的研究结果一致。

image-20240909224900984

关于泛化性能的研究：为了计算泛化误差，作者使用了推导出的泛化误差上界。我们分别使用AdamW、AdamW-D、L2-Adam和L2-Adam-D训练了ResNet18、ResNet50和ViT-small这三个模型，并调优了它们的超参数，包括学习率和权重衰减参数。结果表明，AdamW和AdamW-D的泛化误差显著小于L2-Adam和L2-Adam-D。

关于收敛性能的研究：我们绘制了AdamW、AdamW-D、L2-Adam和L2-Adam-D在ImageNet上的训练和测试曲线。结果表明，当权重衰减参数调优得当时，AdamW和AdamW-D的收敛速度快于L2-Adam（包括将Adam视为 的情况）。此外，AdamW和AdamW-D表现出类似的收敛行为，这意味着权重衰减参数对优化器的收敛速度有显著影响。

VII 总结实验结果验证了AdamW在收敛速度和泛化能力上的优越性。与L2-Adam相比，AdamW不仅表现出更快的收敛速度，而且在各种测试场景下展现了更好的泛化性能。通过这些实验，作者成功证明了AdamW优化算法在深度学习任务中的有效性，并支持了之前的理论分析 。

往期精彩回顾




适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑

• 交流群

欢迎加入机器学习爱好者微信群一起和同行交流，目前有机器学习交流群、博士群、博士申报交流、CV、NLP等微信群，请扫描下面的微信号加群，备注：”昵称-学校/公司-研究方向“，例如：”张小明-浙大-CV“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~（也可以加入机器学习交流qq群772479961）