线性与非线性规划
- 一、线性规划(LP)
- 二、线性规划问题解的概念:
- 三、图解法
- 四、单纯形法
- 单纯形法计算步骤:
- 五、化标准型
- 六、单纯形表
- 七、单纯形表的衍生(人工变量法)
- 7.1 大M法
- 7.2 两阶段法
一、线性规划(LP)
数学模型都是求一组非负解,在满足一组以线性等式或线性不等式所表示的限制条件下,使一个线性函数取得最优值(最大值或者最小值)
标准型:
m
a
x
z
=
∑
j
=
1
n
c
j
x
j
s
.
t
.
∑
j
=
1
n
a
i
j
x
j
=
b
j
(
i
=
1
,
2
,
3...
)
s
.
t
.
x
j
≥
0
(
j
=
1
,
2
,
3...
)
max z=\sum_{j=1}^{n}{c_jx_j}\\ s.t.\sum_{j=1}^{n}{a_{ij}x_j}=b_j\\(i=1,2,3...) s.t.x_j\geq0(j=1,2,3...)
maxz=j=1∑ncjxjs.t.j=1∑naijxj=bj(i=1,2,3...)s.t.xj≥0(j=1,2,3...)
其中,
a
i
j
、
b
i
、
c
j
a_{ij}、b_i、c_j
aij、bi、cj都是确定的常数,
x
j
x_j
xj称为决策变量,z为目标函数,
a
i
j
a_{ij}
aij称为技术系数,
b
i
b_i
bi称为资源系数、
c
j
c_j
cj称为价值系数
二、线性规划问题解的概念:
可行解、基、基可行解、可行基
这里面要先明白可行解的概念,毋庸置疑,在方程中满足约束条件的解称为可行解,其中目标函数值达到最大称为最优解;
如果有B的系数矩阵是m*m的非奇异矩阵,那么B就是基;
满足非负条件的基解,称为基可行解;
基可行解的基称为可行基;
下面图解释一下不同解之间的关系:

三、图解法
适用于两个决策变量
思路:
-
先在直角坐标系平面上画出可行域;
-
其中,非负约束确定了可行域必在第一象限,所求最优解是使目标函数取得最优的可行域上的点
结论:
- 两个变量线性规划的可行域一般是凸多边形;若存在最优解一定可在可行域的某顶点上找到;
- LP约束条件所构成的集合是一凸集合,两个变量时为凸多边形;
四、单纯形法
1、思路1:从线性方程组中找出一个个的单纯形,每一个单纯形可以求得一组解,然后再判断该解使目标函数值是增大还是变小,决定下一步选择的单纯形。这就是迭代,直到目标函数实现最大值或最小值为止。最终得到最优解。
基本思想2:从一个初始基可行解出发,每次选一个非基变量(入基变量)来取代一个基变量(出基变量),也就是说,把一个非基变量从0增加到某一个正数,而把相应的一个基变量从一个正数变为0,多次迭代,最终得到最优解。
单纯形法计算步骤:
- 将线性规划问题化成标准型 (引入松弛变量)
- 找出或构造一个m阶单位矩阵作为初始可行基,建立初始单纯形表。
- 计算各非基变量的检验数$σj=c_j−z_j $若所有检验数≤0,则问题已得到最优解,停止计算。否则,转入下一步。(检验数)
- 在大于0的检验数中,若某个检验数对应的系数列向量≤ 0,则此问题是无界解,停止计算,否则转入下步。
- 根据max(检验数j | 检验数j>0)=检验数k的原则,确定为换入变量(进基变量) 再按最小比值法则( b i a i k b_ia_{ik} biaik,& a i k a_{ik} aik>0)确定换出变量,建立新的单纯形表,此时的基变量中 x k x_k xk代替的换出变量的位置。
- 以 a i k a_{ik} aik为主元素进行迭代,把 x k x_k xk所对应的列向量变为单位列向量,即 a i k a_{ik} aik变为1 同列中其他元素变为0,继续计算各非基变量的检验数,进行第三步。
2、例:
- 化标准型

-
系数矩阵可以写成:
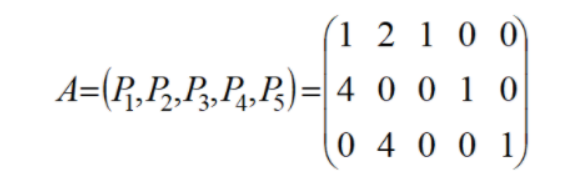
-
我们可以发现以 x 3 , x 4 , x 5 x_3,x_4,x_5 x3,x4,x5的系数可以构成单位矩阵,我们可以以 x 3 , x 4 , x 5 x_3,x_4,x_5 x3,x4,x5为基变量,可以化成:
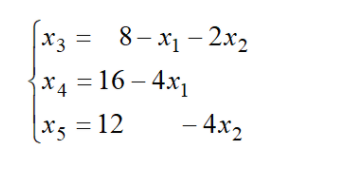
使非基变量 x 1 = 0 , x 2 = 0 x_1=0,x_2=0 x1=0,x2=0
可以得出,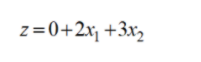
我们此时可以得到一个基解:X(0)=(0,0,8,16,12)T
只要在目标函数的表达式中还存在有正系数的非基变量,这表示目标函数值还有增加的可能,就需要将非基变量与基变量进行对换。
x 2 与 x 5 x_2与x_5 x2与x5进行变换,

**以此类推,**求得
X
(
2
)
X^{(2)}
X(2)=(2,3,0,8,0)T,
X
(
3
)
X^{(3)}
X(3)=(4,2,0,0,4)T
z
=
14
−
1.5
x
3
−
0.125
x
4
z=14−1.5x_3− 0.125x_4
z=14−1.5x3−0.125x4
五、化标准型
1、标准式目标函数为最大值,约束条件为等式、右端项为非负、决策变量取值非负:
例:

2、向量形式
m
a
x
z
=
∑
j
=
1
n
c
j
x
j
s
.
t
.
∑
j
=
1
n
a
i
j
x
i
=
b
j
(
i
=
1
,
2
,
3...
)
s
.
t
.
x
j
≥
0
(
j
=
1
,
2
,
3...
)
max z=\sum_{j=1}^{n}{c_jx_j}\\ s.t.\sum_{j=1}^{n}{a_{ij}x_i}=b_j(i=1,2,3...)\\ s.t.x_j\geq0(j=1,2,3...)
maxz=j=1∑ncjxjs.t.j=1∑naijxi=bj(i=1,2,3...)s.t.xj≥0(j=1,2,3...)
目标函数变为:
m
a
x
z
=
z
0
+
∑
j
=
m
+
1
n
δ
j
x
j
max z=z_0+\sum_{j=m+1}^{n}{\delta_jx_j}
maxz=z0+j=m+1∑nδjxj
其中,
z
0
=
∑
i
=
1
m
c
i
b
i
δ
j
=
c
j
−
∑
i
=
1
m
c
i
a
i
j
z_0=\sum_{i=1}^{m}{c_ib_i}\\ \delta_j=c_j-\sum_{i=1}^{m}{c_ia_{ij}}
z0=i=1∑mcibiδj=cj−i=1∑mciaij
δ
j
\delta_j
δj称为检验数
六、单纯形表

例题:

①先引入三个松弛变量,构造单位矩阵。

得到单位矩阵,构造出初始可行基B

从中我们可以得到信息:基向量组B和非基向量组N
还可以知道所有变量的系数所组成的向量C和基变量 X B X_B XB、非基变量 X N X_N XN:


刚开始,基变量的系数全为0,所以Z=0,Zj=0,可以写出对应的检验数:
可以看出,x2对应的检验数最大,成为换入变量,而且根据最小值法则,知道s3是换出变量。于是将s3的位置换上x2,对应的系数也变成了100。

我们再进行初等行变换,使 x 2 , s 1 , s 2 x_2,s_1,s_2 x2,s1,s2对应的基矩阵变成单位矩阵。在此基础上进行计算 Z j Z_j Zj,就可以利用其算出新一轮的检验数:

我们可以发现,仍然存在检验数大于0的情况,唉,只能进入新一轮的迭代,x1作为换入变量,而经过最小比值规则,可以判定出s1是换出变量

然后,我们再根据新的数据,写出新一轮的Zj和 检验数 ,发现此时的检验数全部≤0,我们成功地找到了最优解!

表格中,检验数全部≤0,根据判断规则,Z值为最优值(Z=27500)
七、单纯形表的衍生(人工变量法)
原始线性规划:
m
a
x
z
=
∑
j
=
1
n
c
j
x
j
s
.
t
.
∑
j
=
1
n
a
i
j
x
j
=
b
i
(
i
=
1
,
2
,
3...
)
s
.
t
.
x
j
≥
0
(
j
=
1
,
2
,
3...
)
max z=\sum_{j=1}^{n}{c_jx_j}\\ s.t.\sum_{j=1}^{n}{a_{ij}x_j}=b_i(i=1,2,3...)\\ s.t.x_j\geq0(j=1,2,3...)
maxz=j=1∑ncjxjs.t.j=1∑naijxj=bi(i=1,2,3...)s.t.xj≥0(j=1,2,3...)
其中,约束方程组中的系数矩阵不含m阶单位阵
故,引入m个人工变量
x
n
+
i
x_{n+i}
xn+i,得到新约束方程组
s
.
t
.
∑
j
=
1
n
a
i
j
x
j
+
x
n
+
i
=
b
i
(
i
=
1
,
2
,
3...
)
s
.
t
.
x
j
≥
0
(
j
=
1
,
2
,
3...
)
s.t.\sum_{j=1}^{n}{a_{ij}x_j+x_{n+i}}=b_i(i=1,2,3...)\\ s.t.x_j\geq0(j=1,2,3...)
s.t.j=1∑naijxj+xn+i=bi(i=1,2,3...)s.t.xj≥0(j=1,2,3...)
对上述新规划问题进行单纯形迭代后,若最优解中每个人工变量取值皆为0,则删去它们后,即可得原线性规划的最优解;若至少有一个人工变量取值大于0,则原规划无可行解
7.1 大M法
由于人工变量在最优解中一律取0值,故,可通过引入一个称为罚因子的大正数M,进行修正,即
m
a
x
z
=
∑
j
=
1
n
c
j
x
j
−
M
∑
i
=
1
m
x
n
+
i
s
.
t
.
∑
j
=
1
n
a
i
j
x
j
+
x
n
+
i
=
b
i
(
i
=
1
,
2
,
3...
)
s
.
t
.
x
j
≥
0
(
j
=
1
,
2
,
3...
)
max z=\sum_{j=1}^{n}{c_jx_j}-M\sum_{i=1}^{m}{x_{n+i}}\\ s.t.\sum_{j=1}^{n}{a_{ij}x_j+x_{n+i}}=b_i(i=1,2,3...)\\ s.t.x_j\geq0(j=1,2,3...)
maxz=j=1∑ncjxj−Mi=1∑mxn+is.t.j=1∑naijxj+xn+i=bi(i=1,2,3...)s.t.xj≥0(j=1,2,3...)
若最优解中含有取正值的人工变量,目标函数不能实现最大化;罚因子的作用:迫使所有的人工变量最终取值均为零。
7.2 两阶段法
第一阶段,求初始基可行解:在原线性规划问题中加入人工变量,使约束矩阵出现单位子矩阵,然后以这些人工变量之和W求最小为目标函数,构造如下模型:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kY8qjW47-1638106249224)(C:\Users\28960\AppData\Roaming\Typora\typora-user-images\image-20211128212814741.png)]
对上述模型求解(单纯形法),若W=0,说明问题存在基本可行解,可以进行第二个阶段;否则,原问题无可行解,停止运算。
**第二阶段:**在第一阶段的最终表中,去掉人工变量,将目标函数的系数换成原问题的目标函数系数,作为第二阶段计算的初始表(用单纯形法计算)。























 4157
4157











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








