稠密(Dense)架构与稀疏(Sparse,以MoE为代表)架构的差异
flyfish
各词的词性与含义
(1)Dense(形容词)
含义:表示 “密集的、稠密的”,描述事物在空间或数量上分布紧凑、数量多。
(2)sparse(形容词)
含义:表示 “稀疏的、稀少的”,与 “Dense” 语义完全相反,描述事物分布松散、数量少。
(3)sparsity(名词)
含义:是 “sparse” 的名词形式,指 “稀疏性”,表示 “稀疏的属性或状态”,而非形容词。
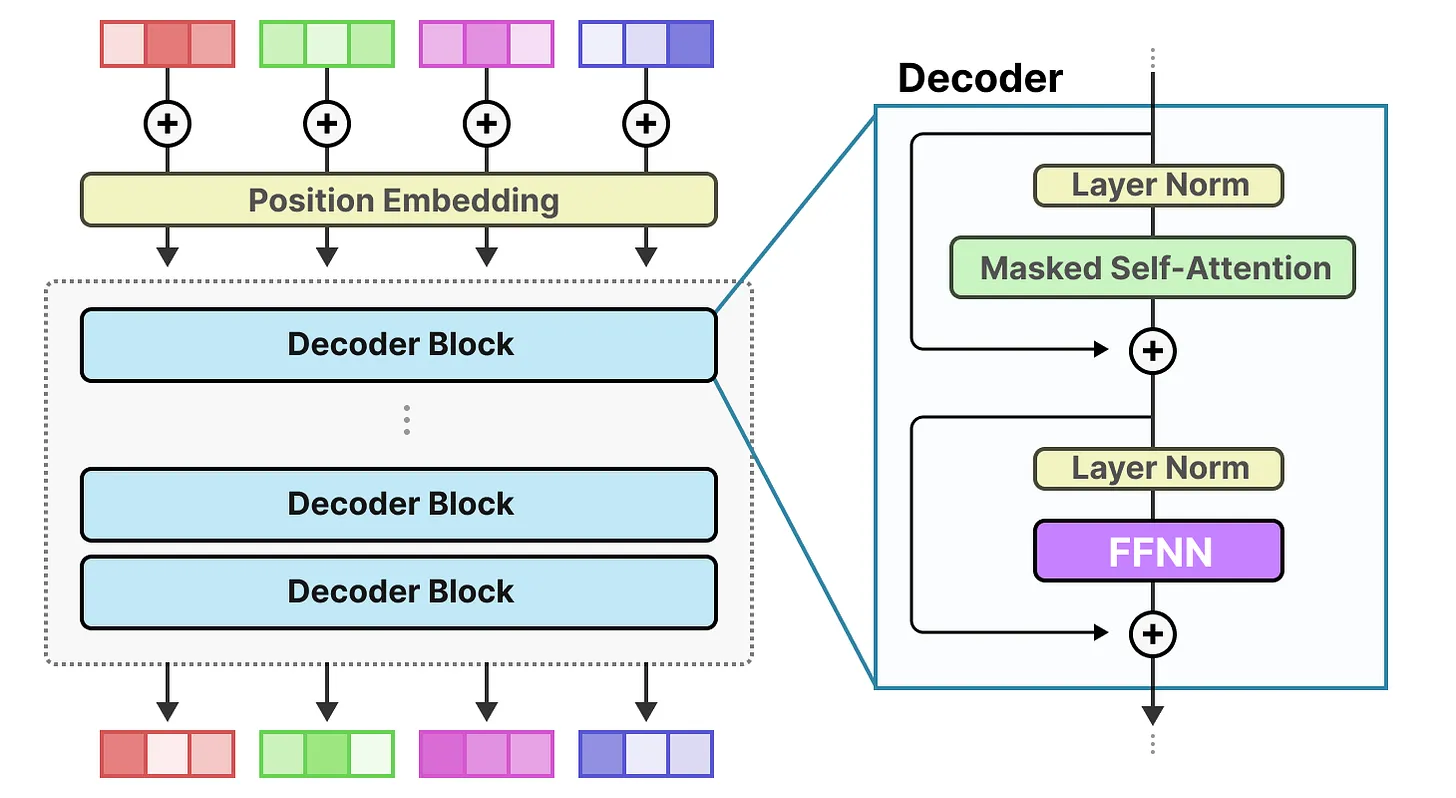
FFNN(Feedforward Neural Network,前馈神经网络)
FFNN(Feedforward Neural Network,前馈神经网络)是一种基础的神经网络架构
1. 定义与结构
“前馈”的本质:数据从「输入层」向「隐藏层」「输出层」单向传递,无循环或反馈连接(信息不会“回头”流动)。
层级组成:
- 输入层:接收原始特征(如图片像素值、文本的词向量表示);
- 隐藏层(可包含多层):对前一层输出进行「加权求和 + 激活函数处理」,实现非线性变换(让网络能学习复杂模式);
- 输出层:生成最终结果(如分类任务的“类别概率分布”、回归任务的“连续预测值”)。
2. 工作原理:“线性变换 + 非线性激活”
每个神经元(节点)的计算分两步:
- 线性变换:接收上一层所有神经元的输出,通过**权重矩阵(( W ))和偏置(( b ))**做加权求和,公式为 ( z = xW + b )(( x ) 为输入);
- 非线性激活:用激活函数(如ReLU、Sigmoid、GeLU等)处理线性结果,引入“非线性能力”(否则多层网络会退化为单层线性模型)。
以Transformer中的经典FFN为例,计算式为:
FFN(x)=f(xW1+b1)W2+b2\text{FFN}(x) = f(xW_1 + b_1)W_2 + b_2FFN(x)=f(xW1+b1)W2+b2
(其中 fff 是激活函数,第一层将输入维度“扩展”,第二层再“还原”维度,实现特征的高效变换)
稠密(Dense)架构与稀疏(Sparse,以MoE为代表)架构的差异
Transformer解码器中稠密(Dense)架构与稀疏(Sparse,以MoE为代表)架构的差异,重点体现**前馈网络(FFNN)的设计变化
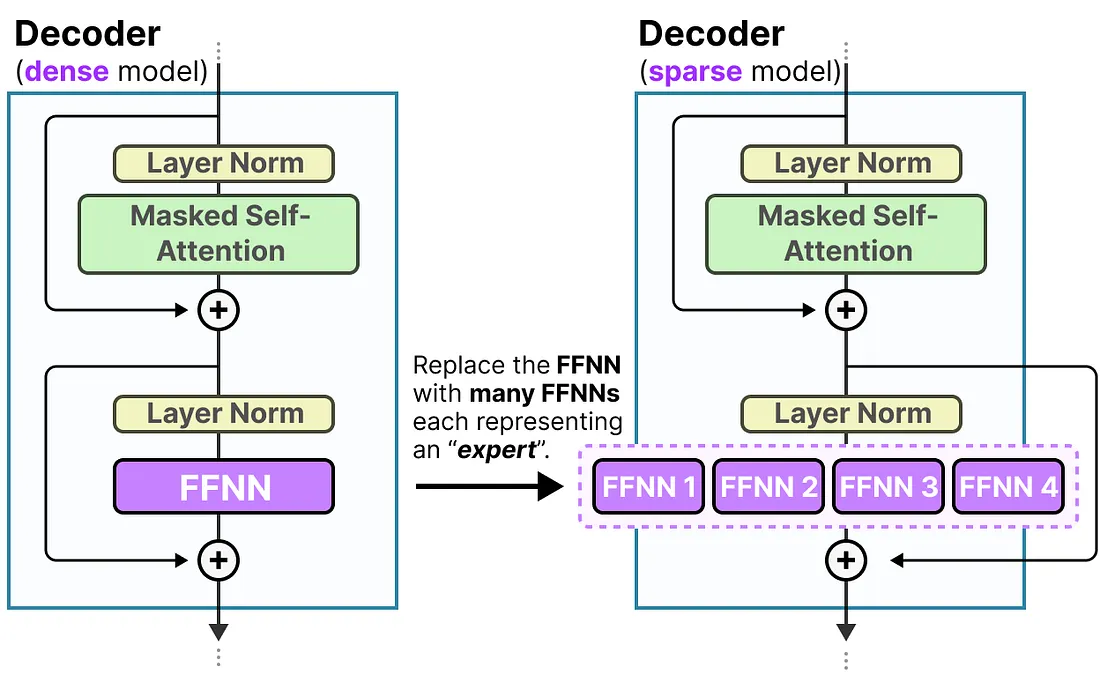
左侧:Dense模型的Decoder结构
这是传统稠密Transformer解码器的典型模块,流程为:
Layer Norm(层归一化,稳定数据分布)→ 2.Masked Self-Attention(掩码自注意力,捕捉序列内的token关联)→ 3. 残差连接(+,避免信息在多层传递中丢失)→ 4.Layer Norm→ 5. 单个FFNN(前馈神经网络) → 6. 残差连接 → 输出。
所有输入都会经过同一个FFNN处理,没有“选择性激活”——FFNN是“全局且唯一的”,所有参数全程参与计算(体现“稠密”的本质:全参数激活)。
右侧:Sparse模型的Decoder结构(MoE类改造)
变化是Replace the FFNN with many FFNNs each representing an expert 将单个FFNN 替换为多个FFNN(每个代表一个专家子网络),流程调整为:
- 前序步骤(
Layer Norm、Masked Self-Attention、残差连接)与左侧一致; - 注意力层输出后,不再进入“单个FFNN”,而是被路由到多个“专家FFNN”(图中为FFNN 1~4);
- 只有与当前输入最匹配的少数专家FFNN会被激活计算(未被选中的专家“休眠”,不消耗算力);
- 激活的专家FFNN输出经整合(残差连接)后,得到最终结果。
设计逻辑
从“全稠密计算”到“稀疏条件计算”的改造:
- Dense架构:用单个FFNN处理所有任务,泛化性强但算力消耗大(全参数激活);
- Sparse(MoE类)架构:用多个“专家FFNN”替代单个FFNN,通过“选择性激活专家”实现“稀疏计算”——既保留多任务能力,又大幅降低算力开销(仅少数专家工作)。
MoE 模型(Mixture of Experts,混合专家模型)
MoE 模型是一种稀疏条件计算架构,核心思想是 “分工与选择性激活”,由两大关键组件构成:
专家子网络(Expert Subnetworks):多个专业化的子模型(通常为 FFN 结构),每个 “专家” 被设计为专精于某一类任务或特征空间(如逻辑推理、文本生成、代码理解等);
门控网络(Gating Network):轻量级决策模块,负责分析输入并动态选择 “最匹配的少数专家子网络” 参与计算(未被选中的专家处于 “休眠” 状态,不消耗算力)。
流程对比
1. Dense模型的计算流程
输入序列(如自然语言文本)经分词(Tokenization)后,依次流经Transformer的编码器/解码器层:
- 每层先通过自注意力(Self-Attention)捕捉序列内关联;
- 随后进入全连接前馈网络(Dense-FFN),此时FFN的所有参数被激活,对注意力层输出的特征进行高维映射与变换;
- 经层归一化(Layer Norm)与残差连接后,传递至下一层,最终生成输出。
简言之,Dense模型的计算是全参数串行激活的流程:输入 → 注意力层 → 全参数FFN → 层归一化&残差连接 → 下一层… → 输出。
2. MoE模型的计算流程
输入序列经分词后进入Transformer层,核心差异体现在FFN阶段:
- 注意力层输出先传递至门控网络,门控网络通过可学习权重与激活函数(如Softmax、Noisy Top-k等),计算输入与每个专家子网络的“匹配分数”;
- 根据匹配分数,仅选择Top-k个专家子网络(如k=2)进行激活,其余专家不参与计算;
- 被激活的专家子网络对输入特征进行处理,各自输出中间结果;
- 门控网络根据“匹配分数”对专家输出进行加权求和,再经层归一化与残差连接后传递至下一层。
简言之,MoE的计算是门控选专家→稀疏激活计算→加权整合的流程:输入 → 注意力层 → 门控网络选专家 → 少数专家FFN计算 → 加权整合 → 层归一化&残差连接 → 下一层… → 输出。
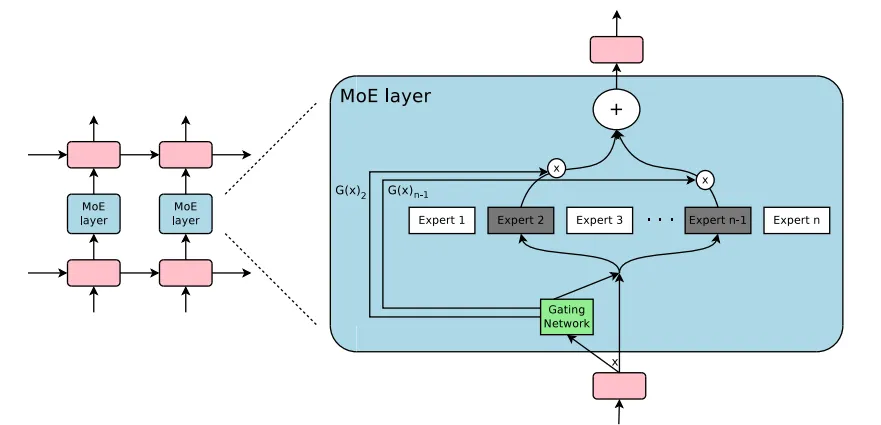
混合专家模型(Mixture of Experts, MoE)的架构
可从多层堆叠和“单MoE层内部逻辑两部分看
1. 整体结构:MoE层的“可堆叠性”
左侧显示 多个MoE层能像传统神经网络层一样“级联堆叠”,构建更深的模型。每一层都可根据输入动态选择专家,让信息在多层中逐步处理、提炼(类似普通神经网络的“层级特征提取”,但每层都有“动态选专家”的智能性)。
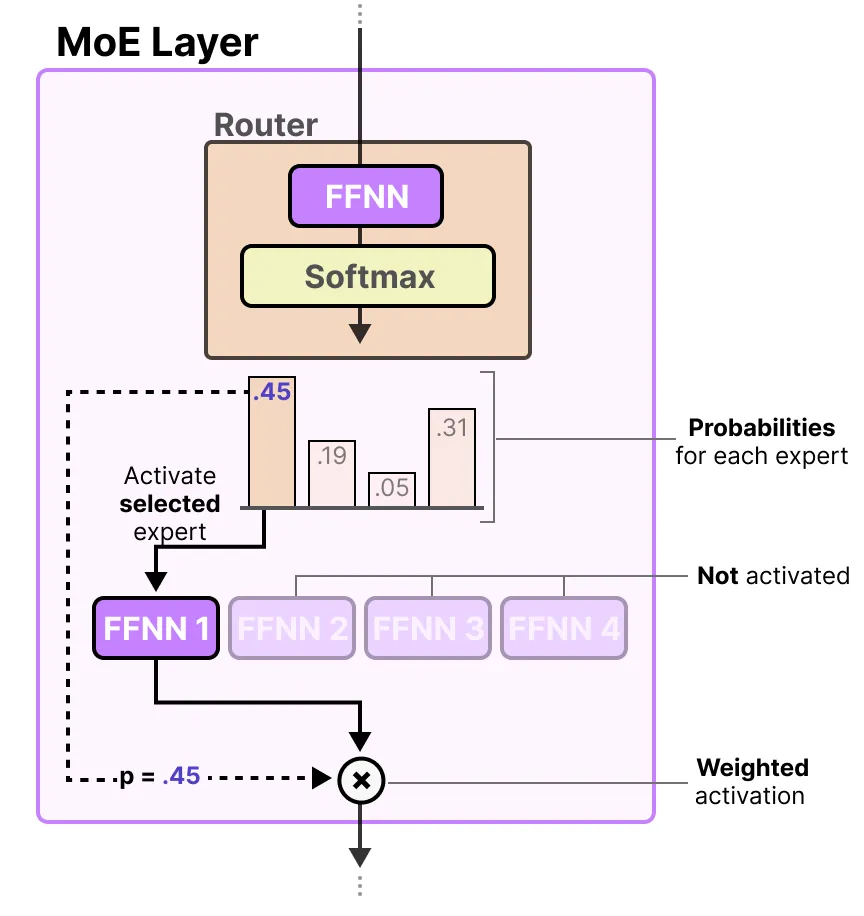
2. 单个MoE层的内部逻辑(右侧放大区域)
单个MoE层是核心,通过“门控选专家 → 专家计算 → 加权整合”的流程,实现“按需调用专家”的高效计算,包含三大关键组件:
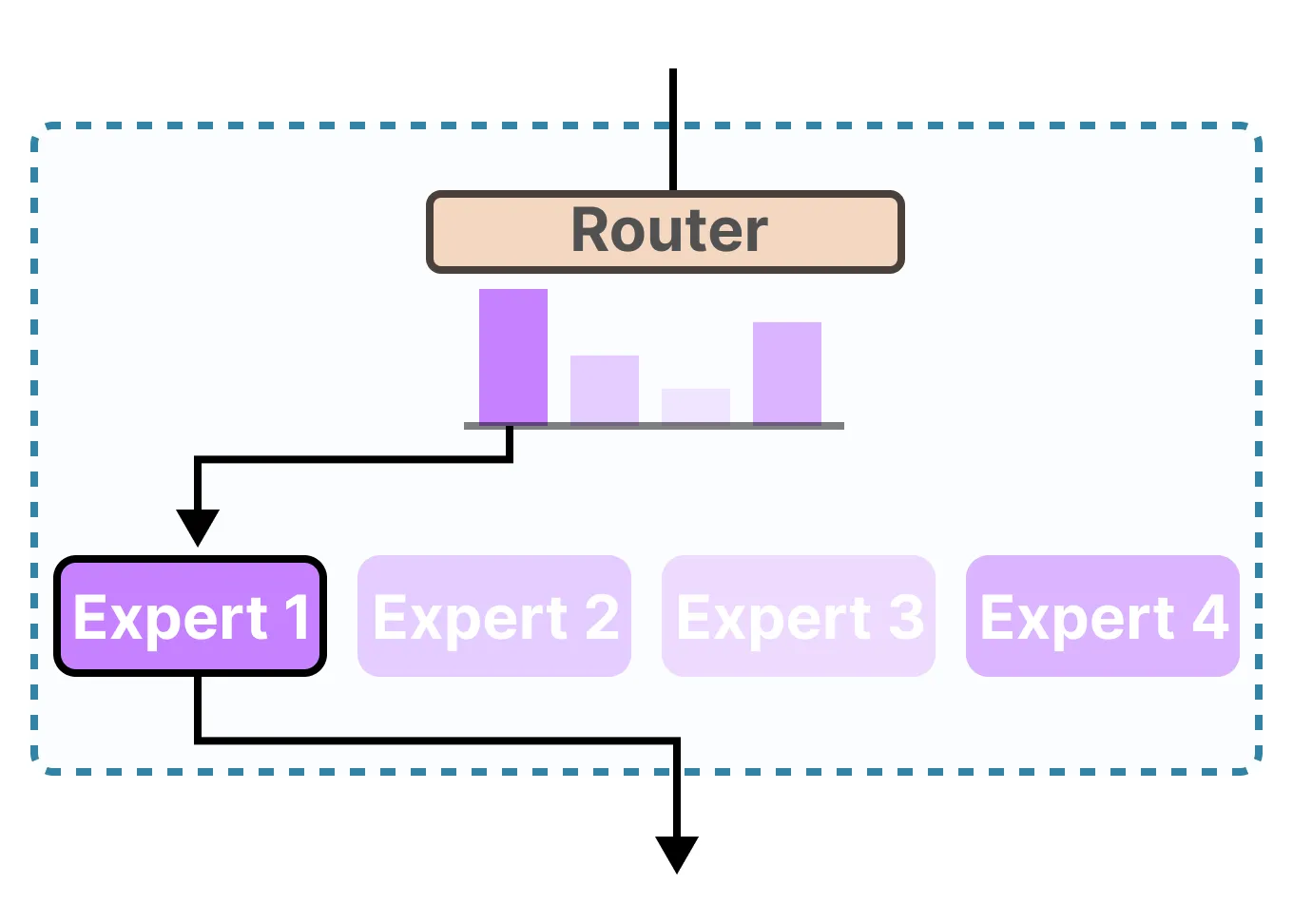
(1)Gating Network(门控网络)
角色:“决策调度器”。
功能:接收输入(下方粉色方块),计算“每个专家子网络与当前输入的匹配程度”,输出“匹配分数”(如图中 G(x)2G(x)_2G(x)2、G(x)n−1G(x)_{n-1}G(x)n−1 等)。
特点:是轻量级网络,参数少、计算快,负责“选谁来干活”。
(2)Expert Subnetworks(专家子网络)
角色:“专项执行者”。
功能:每个“Expert”是专精于某类任务的子模型(比如有的擅长逻辑推理,有的擅长文本生成)。
特点:数量可灵活设置(图中为 Expert 1∼n\text{Expert } 1 \sim nExpert 1∼n),但每次仅激活少数专家(图中深色标注的 Expert 2\text{Expert } 2Expert 2、Expert n−1\text{Expert } n-1Expert n−1 是被选中的专家,其余专家“休眠”,不消耗算力)。
(3)加权整合输出
过程:门控网络的“匹配分数”作为权重,与对应专家的输出相乘(“×”表示“加权”),再通过“+”求和整合,得到MoE层的最终输出(上方粉色方块)。只有被选中的专家会参与计算,体现了MoE的**“稀疏激活”特性**——用“少数专家的计算”替代“全量专家的冗余消耗”,既省算力又保性能。
学习型门控网络(Gating Network)
为了高效分配输入到专家,MoE引入 门控网络(Gating Network, GGG):它通过学习,决定把输入的哪部分发给哪些专家(EEE)。
MoE的输出公式为:
y=∑i=1nG(x)i⋅Ei(x)y = \sum_{i=1}^n G(x)_i \cdot E_i(x)y=i=1∑nG(x)i⋅Ei(x)
- yyy:模型最终输出;
- G(x)iG(x)_iG(x)i:门控网络给第iii个专家的“分配权重”;
- Ei(x)E_i(x)Ei(x):第iii个专家对输入xxx的处理结果。
如果某个专家的权重 G(x)i=0G(x)_i = 0G(x)i=0,该专家就不会参与计算——从而节省算力。
最传统的门控网络是“带Softmax的简单网络”,公式为:
Gσ(x)=Softmax(x⋅Wg)G_\sigma(x) = \text{Softmax}(x \cdot W_g)Gσ(x)=Softmax(x⋅Wg)
- WgW_gWg:门控网络的可学习权重矩阵;
- Softmax的作用:让权重“归一化”(所有专家的权重总和为1),从而明确“输入该优先分配给哪些专家”。
门控网络会在训练中逐渐学习“如何为不同输入选择最合适的专家”。
带噪声的Top-k门控(Noisy Top-k Gating)
1. 从传统Softmax门控说起
传统MoE的门控函数是简单的Softmax:
Gσ(x)=Softmax(x⋅Wg)G_\sigma(x) = \text{Softmax}(x \cdot W_g)Gσ(x)=Softmax(x⋅Wg)
(WgW_gWg是门控网络的可学习权重,输出每个专家的“分配概率”)。
但这种方式容易导致“少数专家被频繁调用,多数专家闲置”,因此需要更智能的门控策略。
2. Noisy Top-k Gating的三步流程
Shazeer等人提出的“带噪声的Top-k门控”分三步,是**“加噪声→选Top-k→Softmax归一化”**:
步骤1:添加噪声(Noise Injection)
对每个专家的“基础门控得分”(由x⋅Wgx \cdot W_gx⋅Wg计算)添加随机噪声:
H(x)i=(x⋅Wg)i+StandardNormal()⋅Softplus((x⋅Wnoise)i)H(x)_i = (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{\text{noise}})_i)H(x)i=(x⋅Wg)i+StandardNormal()⋅Softplus((x⋅Wnoise)i)
- (x⋅Wg)i(x \cdot W_g)_i(x⋅Wg)i:第iii个专家的“基础匹配得分”;
- StandardNormal()\text{StandardNormal}()StandardNormal():生成标准正态分布的随机数(引入随机性);
- Softplus((x⋅Wnoise)i)\text{Softplus}((x \cdot W_{\text{noise}})_i)Softplus((x⋅Wnoise)i):对“噪声权重得分”做平滑处理(确保噪声的缩放为正,避免负向干扰)。
目的:通过噪声让门控选择更“随机”,避免门控网络“固化”地只选少数专家,从而平衡各专家的负载(防止部分专家忙到爆、部分专家闲置)。
步骤2:保留Top-k个专家(Keep Top-k Experts)
对加噪声后的得分向量v=H(x)v = H(x)v=H(x),只保留前kkk大的元素,其余设为−∞-\infty−∞:
KeepTopK(v,k)i={vi若 vi 是 v 中前 k 大的元素,−∞否则.\text{KeepTopK}(v, k)_i = \begin{cases}
v_i & \text{若 } v_i \text{ 是 } v \text{ 中前 } k \text{ 大的元素}, \\
-\infty & \text{否则}.
\end{cases}KeepTopK(v,k)i={vi−∞若 vi 是 v 中前 k 大的元素,否则.
效果:只有前kkk个专家会获得“有效得分”,其余专家的得分在后续Softmax中会被“压制”(因为Softmax对−∞-\infty−∞的输出接近0),相当于只激活Top-k个专家。
步骤3:应用Softmax归一化
对“保留Top-k后的得分”做Softmax,得到最终的门控权重:
G(x)=Softmax(KeepTopK(H(x),k))G(x) = \text{Softmax}(\text{KeepTopK}(H(x), k))G(x)=Softmax(KeepTopK(H(x),k))
让Top-k个专家的权重“归一化”(总和为1),用于后续“专家输出的加权求和”。
若kkk很小(如k=1k=1k=1或k=2k=2k=2),每次仅激活极少数专家,训练和推理速度会远快于“激活大量专家”的情况。
为了负载均衡——防止门控网络“偷懒”式地总选少数专家,让所有专家都有机会被调用,提升整体资源利用率。
Noisy Top-k Gating通过“加噪声→选Top-k→Softmax”的流程,保证了MoE的“稀疏激活(只调用少数专家)”效率,解决“专家负载不均”的问题。























 3248
3248

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










