反向传播(BPTT)与循环神经网络(RNN)文本预测
BPTT 与 RNN文本预测
参考博客:
- http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/
- http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-2-implementing-a-language-model-rnn-with-python-numpy-and-theano/
参考论文:
- A guide to recurrent neural networks and backpropagation
本文介绍简单Recurrent Neural Networks(RNN)的基本训练算法BACKPROPAGATION THROUGH TIME (BPTT),并用 python2.7 实现RNN的文本预测。
1. RNN训练方法:BACKPROPAGATION THROUGH TIME (BPTT)
基本RNN结构如下所示:
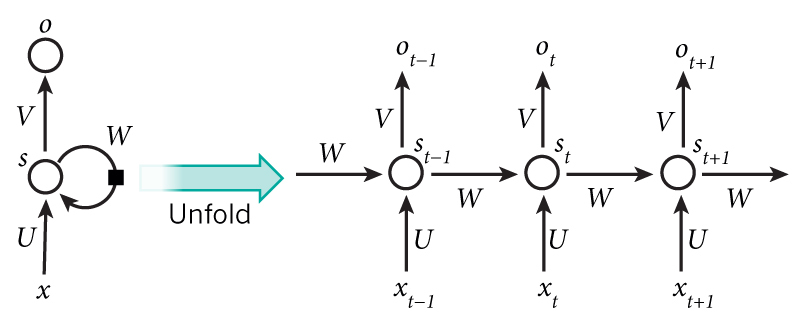
st 是 t 时刻的隐藏状态,它表示网络的记忆单元,由前一时刻的隐藏状态和当前时刻的输入来确定, ot 表示 t 时刻的输出,它与隐藏状态有关:
ot=g(Vst) ,假定 g 为
U,W,V 分别是输入与隐藏状态、先前隐藏状态与当前隐藏状态、隐藏状态与输出之间的连接权重,可分别叫做输入权重、循环权重、输出权重。
BPTT与传统的反向传播算法基本相同,包含如下三个步骤:
(1) 前向传播计算输出 o 和隐藏状态
(2) 反向传播计算误差 δ ,表示模型目标函数 E 对加权输入
(3) 求解模型目标函数
(1) 前向计算
利用如下两式从输入层 xt 计算每层的隐藏状态 s 和 输出
st = f(Uxt+Wst−1) ,假定 f








 本文详细介绍了BPTT(反向传播通过时间)算法在RNN(循环神经网络)中的应用,用于文本预测。讨论了RNN的基本结构,前向传播,误差计算以及权重偏导数的求解。还提到了RNN在处理长序列依赖时的梯度消失或爆炸问题,并探讨了解决策略,如使用ReLU激活函数和LSTM/GRU单元。文中给出了实际的文本预测操作步骤,包括数据预处理、RNN模型的实现和训练。
本文详细介绍了BPTT(反向传播通过时间)算法在RNN(循环神经网络)中的应用,用于文本预测。讨论了RNN的基本结构,前向传播,误差计算以及权重偏导数的求解。还提到了RNN在处理长序列依赖时的梯度消失或爆炸问题,并探讨了解决策略,如使用ReLU激活函数和LSTM/GRU单元。文中给出了实际的文本预测操作步骤,包括数据预处理、RNN模型的实现和训练。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1019
1019

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








