岭回归原理简单分析与理解

岭回归原理简单分析与理解

首先说明一下，岭回归用于回归。学习岭回归，给我的感受是，它的数学公式推导比较简单，然而理解其含义相对难一些，所以本文着重引导你去理解它，而不仅仅是会推导公式。至于背景介绍，网络上很多，这里就不再“复制”了。

这里对数据以及直线方程等全部进行定义与说明，后面就不再重复，直接使用。
现在有一些数据(𝐱_1 , y_1 ) , (𝐱_2 , y_2 ) , … , (𝐱_n , y_n )，其中𝐱_i，i=1 , 2 , … , n 表示第i个样本的一些特征，y_i，i=1 , 2 , … , n 表示第i个样本的数值。
对于拟合的线性方程

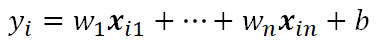
这里，为了使式子变得简化，可以进行一定的变换，令

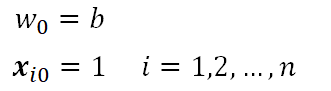
则原线性方程可写成

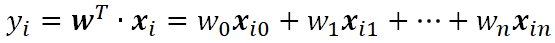
先看一下岭回归的目标函数：

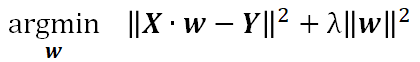
显然，它是在最小二乘的基础之上，在目标函数中增加了后面一项，为了完全弄明白上面这个式子的含义，我们还是先简单说一下最小二乘法。
这里就不介绍背景部分了，直接进入正题，简单介绍最小二乘法。
现在，想一个问题：下面的这些样本，用哪条直线进行拟合比较好？

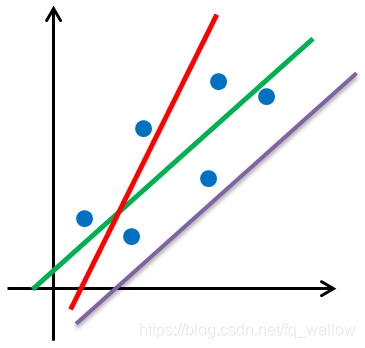
显然，我们会觉得使用绿色的线进行拟合相对来讲更好一些，那么，我们为什么会觉得绿色的这条线，好一些呢？能不能给出一个比较合理的解释呢？
每一个x都对应一个相应的y值，那么，我们可以设计一条直线使得每个x在这个函数上的y‘值与y很接近，当然，如果每个y’与y值都相等是最好的。所以就可以写出目标函数

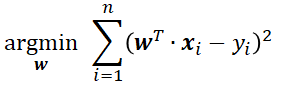
用图形来表示，大概如下图所示（注：此时x是1维的）

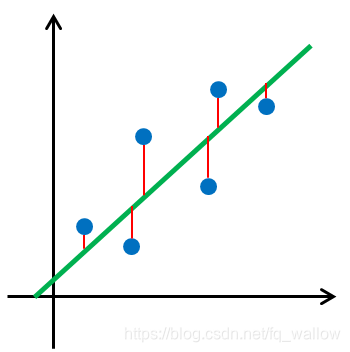
然后，我们再进行求解这个目标函数 ，为了使公式更为简洁，令


则目标函数可以写成

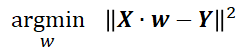
由于这个函数是凸函数，而且是求极小值，所以可以对其求导，导数为0的点，即是极小值点，简化过程（具体如何求导，这里就不仔细讲了）如下

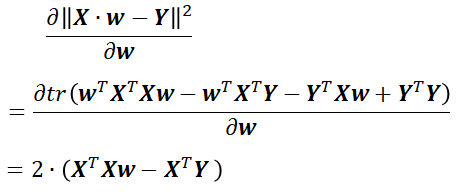
令其导数等于0，得


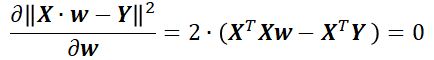
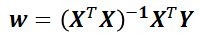
似乎，写到这里，最开始的那个问题就解决了，因为X与Y是训练样本，都已知，完全可以求出w的值。
但是，还有一下几个问题需要考虑

1. 如果X的转置与X的乘积如果不可导，这个方法可行吗？
   答：如果不可导，那这个方法就不太可行。
2. 在什么情况下，X的转置与X的乘积不可导？
   答：假设X是列不满秩的，X的转置与X的乘积就不可导，比如每个样本有N个维度（属性），但训练样本的总个数小于N个。（这只是它不满秩的情况之一，但很常见）
3. 针对不可导的情况，有没有什么比较好的解决办法呢？
   答：岭回归就是专门为解决X的转置与X的乘积不可导而设计的，其具体方法在后面详细介绍。

当然，“天下没有免费的午餐”，解决了某个问题，很可能会出现另外一个问题，但如果另外一个问题的影响不那么大，一般还是可以接受的。
下面是思考过程：
先看一下刚才计算的w

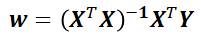
此时的w是理论上的最优解（至于是不是现实的最优解还不一定），但X的转置与X的乘积一般不可导，很可能求不出w。
这个方法还是很好的，不能直接舍弃，那么如何去改进呢？（改进一般比创造新方法相对简单）
最直接的想法就是：既然X的转置与X的乘积一般不可导，那在后面加上一个单位阵，相当于是对w进行小小的扰动，最后得到的w*一般不是最优解，但也比较接近最优解了。（当最优解很难很难求解出来，然而可以较为简单的求出接近最优解的解一般是一种很好的选择）
将刚才解出来的，添加一些扰动（大小由λ控制），变为

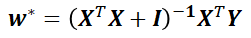
再反推一下目标函数，可以得到

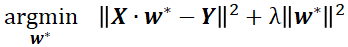
注意：这里，通过增加一个单位阵使得w 有解，从而推出极小化的目标函数只是我个人猜测，仅供参考！
这个含义很明显，就是使得所有的w_i平方和更小，为了更方便理解其具体含义，暂且将其设置成二维的，即w = (w_1 , w_2)，那么该式用图形可表示为

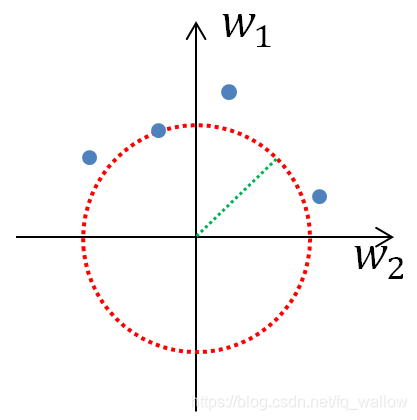
其中，每个蓝色的点表示可以选择的(w_1 , w_2)的值，然后选择其中平方和最小的那一个。
例如，在上面的图中，平方和最小的那个点，显然就是有红色虚线画成的圆上的那个点。
那么，这样选择有什么好处呢？
一般来讲，拟合的线性回归方程中w_i , i = 1 , 2 , … , n 越“简单”，用来预测新的样本时效果更好一些。具体原因，可以了解“奥卡姆剃刀定律”
那么，怎么样才算简单呢？下面看几个例子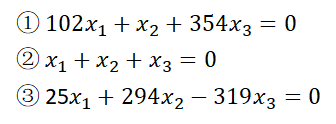
假设这3个式子拟合同一样本，且拟合效果相差不大，那么即便第二个式子的拟合效果差一点点，一般人很可能还是更愿意选择第二条直线当作拟合的直线。（如果相信奥卡姆剃刀定律，那就不要犹豫了，选第二条直线吧）
那么，现在想一下，怎么样才能用数学公式选择出那个更为简单的式子？
思考过程：经过简单观察，第2个式子有个特点，那就是每个变量的系数比较小，那先暂且假设，所有的系数之和越小，函数简单。经过计算，发现第3个式子系数之和等于0，显然，刚才的假设不太好，那现在更改一下假设，所有系数的绝对值之和越小，函数越简单，好像这样假设没什么问题了。但还需要注意的是，计算机计算绝对值的速度比计算平方要慢，所以刚才那个假设，也可以大致等价为，所有系数的平方和越小，函数越简单。
注意：所有思考的最终结果，都不可能绝对完美，所以你才需要学习，然后慢慢改进啊。毕竟，再贵的电脑也有出bug的时候，再完美的人也会有缺点。

上面，理解了岭回归目标函数的后面那个函数（称为L2正则化）的大概含义，下面我们换种方式理解“最小二乘法”目标函数的含义，先来看看这个目标函数

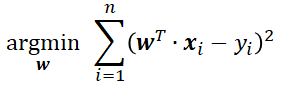
这里的x_i , y_i都是已知的，未知参数只有w，现在换成一种你们最常见的函数的样子。（这里只是为了方便理解，注意：字母含义都变了！）
当w只有1维的，则可以化简为

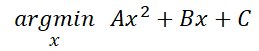
其中A，B，C都是常数。显然，这是一个一元二次方程，然后求它的极小值点（注意：这里的极值点必然是极小值点，想一下为什么？）
函数图像大概如下图所示（蓝色的线）

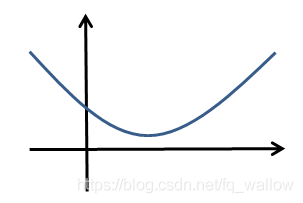
与此同时，再考虑一下另外一个目标函数，可以写成

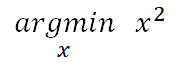
将这个目标函数用红色的线画在上一个图中

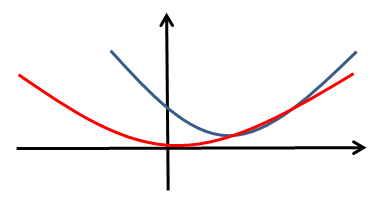
给定一个平衡的常数λ，将两者相加（用绿色的线表示），如下图所示

显然，现在的（绿色线条）极值点比原来的（蓝色线条）极值点，更接近原点O。
再看看二维的情况，这里就不一一计算了，直接上图

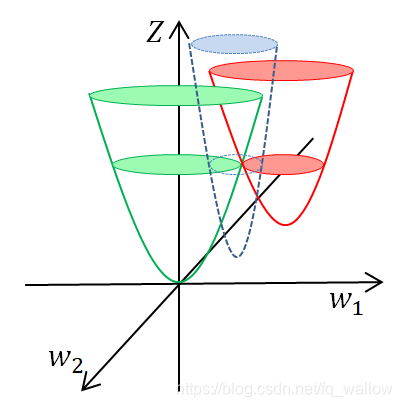
这里解释一下上面那张图的含义，此时考虑的是w = (w_1 , w_2)二维的情况，其中绿色的图形是“最小二乘法”函数的图形，红色的图形是“L2正则化”（也就是岭回归目标函数后面的那个函数）的图形，最后那个虚线蓝色的图形表示给定λ情况下岭回归函数（给定λ，绿色和红色相加）的大致图形。
显然，从图中可以看出，岭回归的极值点比最小二乘法的极值点更接近原点，在“最小二乘法”的基础上，增加一个L2正则项，得到的最优的 w* 更为“简单”（这里再看一下刚才的假设：所有系数的平方和越小，函数越简单）
写到这里，我所理解的岭回归的含义就基本写完了。
接下来，写一下岭回归的计算过程（矩阵求导部分，本文略过）：
目标函数

因为该函数是凸函数，所以极值点就是导数为0的点，先对w求偏导

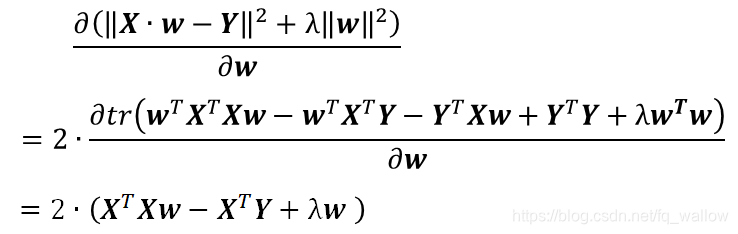
令偏导等于0，有

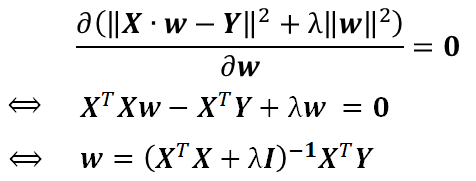
此时，一般情况下w是可以计算出来的（一般不会有不可逆的情况了）。至于特殊情况，那就需要你继续努力的改进了啊！

如果，有什么问题，欢迎留言！