囫囵吞枣电子结构

frank_haha

于 2024-11-25 02:47:50 发布

阅读量1.1k

点赞数 12

分类专栏： AI电子结构预测文章标签：人工智能

本文链接：https://blog.csdn.net/frank_haha/article/details/144017347

版权

AI电子结构预测专栏收录该内容

1 篇文章

订阅专栏

文章目录

前言

大概是2年前，我开始接触计算模拟这个行业，相信和很多人一样，最开始都是去完成实验组的一个合作课题。按照网上的课程（卢天）和师兄导师的指导，使用 Gaussian+MultiWFN （或者凝聚态物理里的 VASP+vaspkit）完成任务。不需要太深的理论知识，跟好网上的帖子即可。

后来，我开始断断续续看一些网课，学校里也上了理论课。教科书十分规整，从最简单的单电子原子结构、均匀电子气模型，讲到复杂的 HF, DFT, 微扰理论。上完课依然云里雾里的，感觉自己了解了一些名词，好像是能按照 PPT 串起来了，但又不知道这些知识除了考试外有什么用，因为实际操作起来依然是无脑的 Gaussian+MultiWFN 组合，时间久了，又慢慢忘掉了。有了一些操作经验后，我开始学文献里搞 “高通量计算”，其实说到底也是写一些自动化脚本，批量提交 Gaussian+MultiWFN 组合，正式成为了业内人士自嘲的 ”熟练的软件操作工“。

直到最近，AI for Science 逐渐进入深水区，研究热点逐渐从原子结构（端到端，无需介入电子结构计算）向电子结构转移，我在做了几个月的相关研究后才逐步重新认识电子结构计算。通过手搓相关代码，对照教科书，对以往的 “深不可测” 的名词有了新的认识。

这篇博客尝试回顾我在这几个阶段对电子结构计算的认识，若有错误，欢迎指正。

实验组眼中的电子结构计算

大部分实验组都有理论支撑的需要，实操起来主要分成如下几步：

使用建模软件 gview/MS 捏出分子/晶体结构，导出结构文件，网上教程很多很详细；

在这里插入图片描述

修改输入文件，把关键词改成已发表文献中提到的参数，或者严谨一些，评测很多泛函基组的组合，选出最贴近实验报道参数的组合（某个键的键长等参数）。
在超算上提交任务，等待任务计算，回收任务结果。
使用 multiwfn 对结果进行分析，照着原贴做就行。

在完成上述步骤后，我们能得到漂亮的电子结构图像，如下图所示：
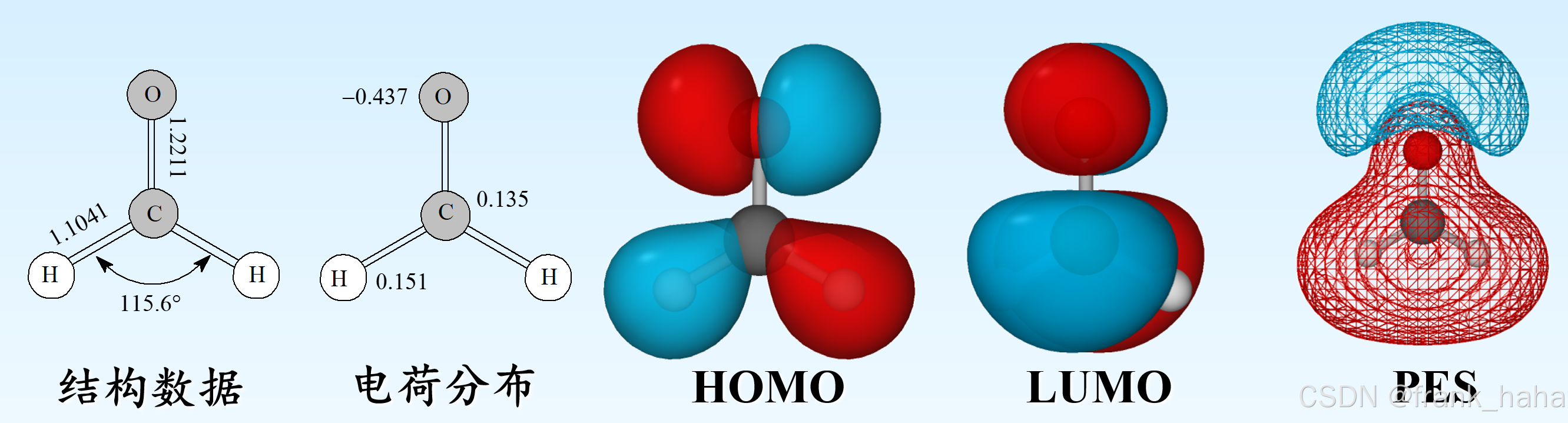
在这里插入图片描述

大部分人都将止步于此，然而，对于那些将计算模拟当成中长期职业发展的人，可能需要自愿或非自愿的啃一些理论课本，大概如下所示。

教科书中的电子结构计算

相信大部分学生拿到课本那一刻，不会觉得这是一门简单的学科。正统教材事无巨细，像一位唠叨的老人，从量子力学诞生那个风起云涌的时代开始讲起。抛去这些宏大的叙事，实用性较强的（也是我现在能回想起的）大概剩下薛定谔方程，以及围绕薛定谔方程的多种解法（泛函），波函数的数值设定（基组）这些。

我们可以切换视角到顶刊论文（例如：2023 NeruIPS QH9），看看计算机背景的人是如何解释电子结构计算的。

薛定谔方程

这篇论文开门见山引入了薛定谔方程，它是处理多电子物理体系的基石。对相关历史感兴趣的话可以去找历史书，在 2024 年的今天，从实用主义者角度出发，我们只需要知道他是基石，跟物理体系的诸多可观测量密切相关。

在这里插入图片描述

方程中 $\hat{H}$ 就是哈密顿算子，他可能包含了很多子项，比如系统的动能、势能，公式推导很复杂，但实际应用里，这个位置就是一个需要求解的二维矩阵。

当哈密顿量固定时，方程就变成了一个广义本征值问题，存在多个满足方程的本征值 $E$ （用于描述整个体系的能量）和本征向量 $\Psi\left(\boldsymbol{r}_{1},\cdots,\boldsymbol{r}_{n}\right)$ （用于描述电子的分布状态，例如分子周围的电子密度）。

然而，通常情况下，即便哈密顿量固定，我们依然无法精确求解该方程。事实上，现在能精确求解的体系只有最简单的单电子原子体系。幸运的是，我们能够利用单电子原子体系的精确解，通过排列组合，线性拟合出复杂的多电子分子体系（含有超过一个电子）的波函数 $\Psi\left(\boldsymbol{r}_{1},\cdots,\boldsymbol{r}_{n}\right)$ ，这种通过已知解近似未知解的方法叫做原子轨道线性组合(LCAO,Linear Combination of Atomic Orbitals) 表示： $\psi_i(\boldsymbol r)=\sum_jC_{ij}\phi_j(\boldsymbol r)$

我们将薛定谔方程中的波函数替换成原子轨道线性组合形式，再经过一同公式变化，得到了更简洁的形式：

请添加图片描述

方程中 $H$ 是一个需要求解的二维矩阵， $C_i$ 是我们做上述替换时的系数，也是一个矩阵， $S$ 跟 “选择什么样的原子轨道波函数” 相关，即，跟计算时用的基组相关，不同的基组对应不同的 $S$ 矩阵，是一个提前定好的矩阵，常数值。最后， $\epsilon_i$ 对应能级，即整个体系能量高低水平，值越小体系越稳定。

自洽场迭代

上一小节，我们使用了原子轨道线性组合理论简化了薛定谔方程，变成了一个广义本征值求解问题。事实上，在计算机从业者眼里（例如：2023 NeruIPS QH9），知道这么多已经够了。

公式 2 里一共 4 个变量：

$S$ 矩阵是一个提前定好的矩阵
$H$ 矩阵是通过 AI 拟合出来的
将 $H$ 和 $S$ 矩阵代入公式 2，求解本征值问题（调包即可）得到配对的能级 $\epsilon_i$ 和系数矩阵 $C_i$

在原子轨道线性组合表示下，系数矩阵 $C_i$ 描述了电子的分布状态，与可观测量直接相连：

得到系数矩阵 $C_i$ 后，代入 $\psi_i(\boldsymbol r)=\sum_jC_{ij}\phi_j(\boldsymbol r)$ 得到分子轨道波函数
所有占据轨道波函数的模值即为电子密度矩阵，在实空间积分后得到实空间电子密度（可观测量）

在梳理这几个变量之间的关系，以及推导顺序以后，我们发现，整个方程的求解是一个单向过程：

提前定好的 $S$ 矩阵+ AI 拟合的 $H$ 矩阵 → 调包解出本征值和本征向量 → 进一步后处理拿到实空间电子密度等可观测量

当然传统教科书里是复杂很多的。具体来说，书里引入了自洽场（self-consistent field, SCF ）方法：

初猜一个系数矩阵 → 配合提前定好的 $S$ 矩阵解出 $H$ 矩阵 → 调包解出新的本征值和本征向量（系数矩阵） → 配合提前定好的 $S$ 矩阵解出新的 $H$ 矩阵 →

如此往复直到收敛。

上述迭代求解系数矩阵的方案是最原始的基于原子轨道线性组合的方案，学界称之为 HF 自洽场方法：

请添加图片描述

该方案最早源自于 1928 年 Hatree 轨道近似思想，最初主要针对简单分子体系。HF 方法的核心：单电子近似会不可避免的引入电子自相关误差。而在 1960 年代发展起来的 DFT （密度泛函理论）则能从原理上避免这一误差，但又会引入新的误差（通常称作交换关联误差）。

两个方案都有误差，通过将 HF 与 DFT 进行掺杂可将误差相互抵消，提高精度，这种就是大家常说的杂化泛函。比如常用的 B3LYP 泛函就是 20% HF+80%DFT 的组合。

DIY 爱好者代码里的电子结构计算

看书学习更深层的计算模拟原理就像迷雾森林里的摸索探险，因为相关公式推导太多了，很难读下去。好在如今有很多编程工具能帮助我们辅助理解这一过程。（因为里面各种积分也是调包）

PySCF 就是这样一款轻量级软件。我们可以借助 ChatGPT 学习使用 PySCF，加深对电子结构计算的认识：

请添加图片描述

import numpy as np
import matplotlib.pyplot as plt
from pyscf import gto, scf, dft, tools

# 1. 定义水分子结构和基组
mol = gto.Mole()
mol.atom = """
O  0.0000  0.0000  0.0000
H  0.0000  0.7570  0.5860
H  0.0000 -0.7570  0.5860
"""
mol.basis = 'def2-svp'  # 使用较准确的基组
mol.charge = 0
mol.spin = 0  # 闭壳层
mol.build()

# 2. 进行SCF计算
mf = scf.RHF(mol)
mf.kernel()

# 获取 HOMO 和 LUMO 信息
homo_idx = mf.mol.nelectron // 2 - 1
lumo_idx = homo_idx + 1
print(f"HOMO: {mf.mo_energy[homo_idx]:.6f} Hartree, LUMO: {mf.mo_energy[lumo_idx]:.6f} Hartree")

# 3. 生成格点文件（拖入 VESTA 即可可视化）
dm = mf.make_rdm1()  # 密度矩阵
tools.cubegen.density(mol, 'electron_density.cube', dm)
homo_coeff = mf.mo_coeff[:, homo_idx]
tools.cubegen.orbital(mol, 'HOMO.cube', homo_coeff)
lumo_coeff = mf.mo_coeff[:, lumo_idx]
tools.cubegen.orbital(mol, 'LUMO.cube', lumo_coeff)

# 4. 可视化重要矩阵
# 4.1 获取哈密顿矩阵和重叠矩阵
Hamiltonian = mf.get_fock()  # 哈密顿矩阵
overlap = mol.intor("int1e_ovlp")  # 重叠矩阵


# 4.2 绘制热图函数
def plot_matrix(matrix, title, filename):
    plt.figure(figsize=(8, 6))
    plt.imshow(matrix, cmap='viridis', interpolation='nearest')
    plt.colorbar(label='Value')
    plt.title(title)
    plt.xlabel("Basis Function Index")
    plt.ylabel("Basis Function Index")
    plt.tight_layout()
    plt.savefig(filename)
    plt.show()


# 4.3 绘制哈密顿矩阵和重叠矩阵的热图
plot_matrix(Hamiltonian, "Hamiltonian Matrix (H_core)", "Hamiltonian_heatmap.png")
plot_matrix(overlap, "Overlap Matrix (S)", "overlap_matrix_heatmap.png")

通过 DIY 编程，我们拿到了 Gaussian+MultiWFN 同样的计算结果，对电子结构计算有了更深刻的认识。

请添加图片描述

AI for Science 时代下的电子结构计算

AI for 计算模拟是近 5 年来兴起的新兴学科，按照是否涉及薛定谔方程，我们可以将其粗略地划分为：原子模型和电子模型。

请添加图片描述

从实用主义视角审视这两种模型，二者优劣如下：

原子模型训练过程中能够有效利用的信息少，仅有结构信息、分子能量、原子受力信息。而电子模型能够有效利用哈密顿量信息，信息密度更高。因而在电子结构相关的性质预测上，电子结构模型优于原子结构模型。这一点已经有了相关的报道。（2025 ICLR under reveiw_WANet）

请添加图片描述

电子结构模型通过预测哈密顿量，能够间接推导出更复杂的空间图像，例如可视化 HOMO-LUMO 轨道、分子静电势等，而原子模型做不了。下面是我最近做的电子结构模型预测碳酸乙酯分子静电势的案例，此外还有人用来预测质子转移过程中的电子密度动态变化（2019_NC_SchNOrb），分子器件工作机理（unpublished_DeepTB-NEGF）
电子结构模型需要准备信息量更丰富的数据集，学习成本高。
推理速度，如果单单预测哈密顿量矩阵，与原子模型速度近似。实测更耗时的地方在于后期求本征值以及计算格点积分。