The Designer
Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 898 Accepted Submission(s): 174
Problem Description
Nowadays, little haha got a problem from his teacher.His teacher wants to design a big logo for the campus with some circles tangent with each other. And now, here comes the problem. The teacher want to draw the logo on a big plane. You could see the example of the graph in the Figure1
At first, haha’s teacher gives him two big circles, which are tangent with each other. And, then, he wants to add more small circles in the area where is outside of the small circle, but on the other hand, inside the bigger one (you may understand this easily if you look carefully at the Figure1.
Each small circles are added by the following principles.
- you should add the small circles in the order like Figure1.
- every time you add a small circle, you should make sure that it is tangented with the other circles (2 or 3 circles) like Figure1.
The teacher wants to know the total amount of pigment he would use when he creates his master piece.haha doesn’t know how to answer the question, so he comes to you.
Task
The teacher would give you the number of small circles he want to add in the figure. You are supposed to write a program to calculate the total area of all the small circles.
Input
The first line contains a integer t(1≤t≤1200), which means the number of the test cases. For each test case, the first line insist of two integers R1 and R2separated by a space (1≤R≤100), which are the radius of the two big circles. You could assume that the two circles are internally tangented. The second line have a simple integer N (1≤N≤10 000 000), which is the number of small circles the teacher want to add.
Output
For each test case:
Contains a number in a single line, which shows the total area of the small circles. You should out put your answer with exactly 5 digits after the decimal point (NO SPJ).
Sample Input
2
5 4
1
4 5
1
Sample Output
3.14159
3.14159
题意：给一个大圆和小圆的半径，小圆内切于大圆，在大圆和小圆的缝隙中加相互相切的n个圆，以如图的方式加求加的n个圆的面积
思路1：若半径为r1、r2、r3的圆内切于半径为r4的圆中，则
——笛卡尔定理
从这个定理求得rk通项
有笛卡尔定理得
(
1
r
k
+
1
+
1
r
k
+
1
R
2
−
1
R
1
)
2
=
2
(
1
r
k
+
1
2
+
1
r
k
2
+
1
R
2
2
+
1
R
1
2
)
\left ( \frac{1}{r_{k+1}}+\frac{1}{r_{k}}+\frac{1}{R_{2}}-\frac{1}{R_{1}}\right )^{2}=2\left (\frac{1}{r_{k+1}^{2}}+\frac{1}{r_{k}^{2}}+\frac{1}{R_{2}^{2}}+\frac{1}{R_{1}^{2}}\right )
(rk+11+rk1+R21−R11)2=2(rk+121+rk21+R221+R121)
类似的
(
1
r
k
−
1
+
1
r
k
+
1
R
2
−
1
R
1
)
2
=
2
(
1
r
k
−
1
2
+
1
r
k
2
+
1
R
2
2
+
1
R
1
2
)
\left ( \frac{1}{r_{k-1}}+\frac{1}{r_{k}}+\frac{1}{R_{2}}-\frac{1}{R_{1}}\right )^{2}=2\left (\frac{1}{r_{k-1}^{2}}+\frac{1}{r_{k}^{2}}+\frac{1}{R_{2}^{2}}+\frac{1}{R_{1}^{2}}\right )
(rk−11+rk1+R21−R11)2=2(rk−121+rk21+R221+R121)
两式相减得
2
(
1
r
k
+
1
−
1
r
k
−
1
)
(
1
r
k
+
1
+
1
r
k
−
1
)
=
(
1
r
k
+
1
−
1
r
k
−
1
)
(
2
r
k
+
1
r
k
+
1
+
1
r
k
−
1
+
2
R
2
−
2
R
1
)
2\left ( \frac{1}{r_{k+1}}- \frac{1}{r_{k-1}}\right )\left ( \frac{1}{r_{k+1}}+\frac{1}{r_{k-1}} \right )=\left ( \frac{1}{r_{k+1}}- \frac{1}{r_{k-1}}\right )\left ( \frac{2}{rk}+\frac{1}{r_{k+1}}+\frac{1}{r_{k-1}}+\frac{2}{R_{2}}- \frac{2}{R_{1}}\right )
2(rk+11−rk−11)(rk+11+rk−11)=(rk+11−rk−11)(rk2+rk+11+rk−11+R22−R12)
⇒
1
r
k
+
1
+
1
r
k
−
1
−
2
r
k
=
2
(
1
R
2
−
1
R
1
)
\Rightarrow \frac{1}{r_{k+1}}+\frac{1}{r_{k-1}}-\frac{2}{r_{k}}=2\left ( \frac{1}{R_{2}} -\frac{1}{R_{1}}\right )
⇒rk+11+rk−11−rk2=2(R21−R11)
⇒
(
1
r
k
+
1
−
1
r
k
)
−
(
1
r
k
−
1
r
k
−
1
)
=
2
(
1
R
2
−
1
R
1
)
\Rightarrow\left ( \frac{1}{r_{k+1}}-\frac{1}{r_{k}} \right )-\left ( \frac{1}{r_{k}}-\frac{1}{r_{k-1}} \right )=2\left ( \frac{1}{R_{2}} -\frac{1}{R_{1}}\right )
⇒(rk+11−rk1)−(rk1−rk−11)=2(R21−R11)
进行累加
令
1
R
2
−
1
R
1
\frac{1}{R_{2}} -\frac{1}{R_{1}}
R21−R11=A
⇒
1
r
k
+
1
−
1
r
k
=
2
A
(
k
−
1
)
+
(
1
r
2
−
1
r
1
)
\Rightarrow\frac{1}{r_{k+1}}-\frac{1}{r_{k}}=2A\left ( k-1 \right )+\left ( \frac{1}{r_{2}}-\frac{1}{r_{1}} \right )
⇒rk+11−rk1=2A(k−1)+(r21−r11)
再次累加
⇒
1
r
k
+
1
=
2
A
[
k
2
−
k
+
k
2
2
]
+
(
1
r
2
−
1
r
1
)
k
+
1
r
1
\Rightarrow\frac{1}{r_{k+1}}=2A\left [ k^{2}-\frac{k+k^{2}}{2} \right ]+\left ( \frac{1}{r_{2}}-\frac{1}{r_{1}} \right )k+\frac{1}{r_{1}}
⇒rk+11=2A[k2−2k+k2]+(r21−r11)k+r11
⇒
1
r
k
+
1
=
A
k
2
+
(
1
r
2
−
1
r
1
−
A
)
k
+
1
r
1
\Rightarrow\frac{1}{r_{k+1}}=Ak^{2}+\left ( \frac{1}{r_{2}}-\frac{1}{r_{1}} -A\right )k+\frac{1}{r_{1}}
⇒rk+11=Ak2+(r21−r11−A)k+r11
⇒
1
r
k
=
A
(
k
−
1
)
2
+
(
1
r
2
−
1
r
1
−
A
)
(
k
−
1
)
+
1
r
1
\Rightarrow\frac{1}{r_{k}}=A\left ( k-1 \right )^{2}+\left ( \frac{1}{r_{2}}-\frac{1}{r_{1}} -A\right )\left ( k-1 \right )+\frac{1}{r_{1}}
⇒rk1=A(k−1)2+(r21−r11−A)(k−1)+r11
⇒
1
r
k
=
A
k
2
+
(
1
r
2
−
1
r
1
−
3
A
)
k
+
2
A
+
2
r
1
−
1
r
2
\Rightarrow\frac{1}{r_{k}}=Ak^{2}+\left ( \frac{1}{r_{2}}-\frac{1}{r_{1}} -3A\right )k+2A+\frac{2}{r_{1}}-\frac{1}{r_{2}}
⇒rk1=Ak2+(r21−r11−3A)k+2A+r12−r21
⇒
r
k
=
1
A
k
2
+
(
1
r
2
−
1
r
1
−
3
A
)
k
+
2
A
+
2
r
1
−
1
r
2
\Rightarrow r_{k}=\frac{1}{Ak^{2}+\left ( \frac{1}{r_{2}}-\frac{1}{r_{1}} -3A\right )k+2A+\frac{2}{r_{1}}-\frac{1}{r_{2}}}
⇒rk=Ak2+(r21−r11−3A)k+2A+r12−r211
其中
r
1
=
R
1
−
R
2
r_{1}=R_{1}-R_{2}
r1=R1−R2,
r
2
=
1
A
+
1
r
1
r_{2}=\frac{1}{A+\frac{1}{r_{1}}}
r2=A+r111
接下来我们可以直接求解了，注意的是这里求得都是单侧的圆的半径，如图这样的圆的半径
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <math.h>
#define eps 1e-13
using namespace std;
const double PI=acos(-1);
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
double R1,R2;
int n;
scanf("%lf%lf%d",&R1,&R2,&n);
if(R2>R1)
swap(R1,R2);
if(R2==R1)
{
printf("0.00000\n");
continue;
}
double A=1.0/R2-1.0/R1;
double r1_=1.0/(R1-R2);
double r2_=r1_+A;
double ans=(1.0/r1_)*(1.0/r1_);
double r;
n--;
for(int i=2,j=1;j<=n;i++,j+=2)
{
r=1.0/(A*i*i+(r2_-r1_-3*A)*i+2*r1_+2*A-r2_);
if(r*r<eps)
break;
ans+=r*r; if(j+1<=n) ans+=r*r;
}
printf("%.5lf\n",ans*PI);
}
return 0;
}
思路2：r1我们可以直接求
r
1
=
R
1
−
R
2
r_{1}=R_{1}-R_{2}
r1=R1−R2
那么我们根据笛卡尔定理得：
(
1
r
1
+
1
r
2
+
1
R
2
−
1
R
1
)
2
=
2
(
1
r
1
2
+
1
r
2
2
+
1
R
2
2
+
1
R
1
2
)
\left ( \frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{R_{2}}-\frac{1}{R_{1}}\right )^{2}=2\left (\frac{1}{r_{1}^{2}}+\frac{1}{r_{2}^{2}}+\frac{1}{R_{2}^{2}}+\frac{1}{R_{1}^{2}}\right )
(r11+r21+R21−R11)2=2(r121+r221+R221+R121)
⇒
−
1
r
2
2
+
2
(
A
+
1
r
1
)
1
r
2
+
(
A
+
1
r
1
)
2
−
2
(
1
r
1
2
+
1
R
2
2
+
1
R
1
2
)
=
0
\Rightarrow -\frac{1}{r_{2}^{2}}+2\left ( A+\frac{1}{r_{1}} \right )\frac{1}{r_{2}}+\left ( A+\frac{1}{r_{1}} \right )^{2}-2\left ( \frac{1}{r_{1}^{2}}+\frac{1}{R_{2}^{2}}+\frac{1}{R_{1}^{2}} \right )=0
⇒−r221+2(A+r11)r21+(A+r11)2−2(r121+R221+R121)=0
这里将
1
r
2
\frac{1}{r_{2}}
r21看作未知数，可解得两个解，我们从图上来看的话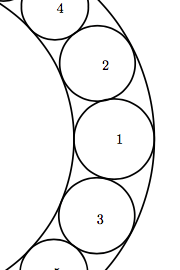
2和3就是这里的解，并且圆2和圆3半径相同，也就是说
x
1
+
x
2
=
−
b
a
x_{1}+x_{2}=-\frac{b}{a}
x1+x2=−ab,
1
r
2
=
A
+
1
r
1
\frac{1}{r_{2}}=A+\frac{1}{r_{1}}
r21=A+r11
我们求得了
r
2
r_{2}
r2那么当要求
r
3
r_{3}
r3时方程是一样的
x
1
+
x
2
=
2
(
A
+
1
r
2
)
x_{1}+x_{2}=2\left ( A+\frac{1}{r_{2}} \right )
x1+x2=2(A+r21)
相当于
1
r
3
+
1
r
1
=
2
(
A
+
1
r
2
)
\frac{1}{r_{3}}+\frac{1}{r_{1}}=2\left ( A+\frac{1}{r_{2}} \right )
r31+r11=2(A+r21)，那么递推公式就有了
⇒
1
r
k
+
1
r
k
−
2
=
2
(
A
+
1
r
k
−
1
)
\Rightarrow \frac{1}{r_{k}}+\frac{1}{r_{k-2}}=2\left ( A+\frac{1}{r_{k-1}} \right )
⇒rk1+rk−21=2(A+rk−11)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <math.h>
#define eps 1e-13
using namespace std;
const double PI=acos(-1);
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
double R1,R2;
int n;
scanf("%lf%lf%d",&R1,&R2,&n);
if(R1<R2)
swap(R1,R2);
double r1_=1.0/(R1-R2);
double A=1.0/R2-1.0/R1;
double r2_=A+r1_;
double ans=(1.0/r1_)*(1.0/r1_);
double r=r2_;
n--;
for(int i=1; i<=n; i+=2)
{
if((1.0/r)*(1.0/r)<eps)
break;
ans+=(1.0/r)*(1.0/r);
if(i+1<=n) ans+=(1.0/r)*(1.0/r);
r=2*(A+r2_)-r1_;
r1_=r2_,r2_=r;
}
printf("%.5lf\n",ans*PI);
}
return 0;
}
152
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
