【交通预测模型】STSGCN

最新推荐文章于 2025-03-16 09:05:33 发布

gao00013

最新推荐文章于 2025-03-16 09:05:33 发布

阅读量1.4k

点赞数 1

文章标签：深度学习人工智能

本文链接：https://blog.csdn.net/gao00013/article/details/134414631

版权

Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting

时空同步图卷积网络:一种新的时空网络数据预测框架

AAAI 2020

摘要

时空网络数据预测在交通管理和城市规划中有着广泛的应用。然而，潜在的复杂时空相关性和异质性使这个问题具有挑战性。现有方法通常使用单独的分量来捕获时空相关性，而忽略了时空数据的异质性。本文提出了一种时空同步图卷积网络(STSGCN)模型，用于时空网络数据预测。该模型通过精心设计的时空同步建模机制，能够有效捕获复杂的局部时空关联。同时，在模型中针对不同时间段设计了多个模块，有效捕捉局部时空图的异质性。在四个真实数据集上进行了广泛的实验，这表明我们的方法达到了最先进的性能，并且始终优于其他基线。

介绍

时空网络数据预测是时空数据挖掘中的一个基础性研究问题。在交通网络、移动基站网络、城市供水系统等现实应用中，时空网络是一种典型的能够描述大量数据的数据结构。准确的时空网络数据预测可以显著提高这些应用的服务质量。随着图上深度学习的发展，图卷积网络及其变体等强大的方法已被广泛应用于这些时空网络数据预测任务中，并取得了良好的性能。然而，目前还缺乏有效的方法来模拟空间和时间方面的相关性和异质性。为了提高时空网络数据预测的准确性，本文重点设计了一个同步捕获复杂时空相关性并考虑异质性的模型。

图1：时空网络中红节点的影响。棕色箭头表示网络的边缘，也表示在空间维度上的影响。蓝色箭头表示红色节点在下一个时间步对自身的影响。绿色箭头表示红色节点与其相邻节点在下一个时间步之间跨空间和时间维度的影响。t1和t2表示两个连续的时间步长。

以图1所示的时空网络为例，该网络中存在三种不同的影响。时空图中的每个节点都可以在同一时间步对相邻节点产生直接影响，这种影响来源于实际的空间依赖关系。同时，由于时间序列中的时间相关性，每个节点也可以在下一个时间步直接影响自己。此外，由于同步的时空相关性，每个节点甚至可以在下一个时间步直接影响相邻节点，如图1所示。三种不同影响存在的原因是信息在时空网络中的传播同时沿着空间和时间维度发生。由于节点间空间距离和时间序列时间范围的限制，这些复杂的时空相关性通常是局部化的。我们把这些复杂的影响称为局部时空相关性。这种相关性建模对于时空网络数据预测至关重要。

之前的研究，如DCRNN (Li et al . 2017)、STGCN (Yu, Yin, and Zhu 2018)和ASTGCN (Guo et al . 2019a)分别使用两个独立的组件来捕获时间和空间依赖性。这些方法只直接捕捉到我们上面提到的前两种影响，即空间依赖性和时间相关性。它们将空间表示输入到时间建模模块中，以间接捕获第三种影响。然而，我们相信，如果这些复杂的局部时空相关性可以同时被捕获，它将非常有效地用于时空数据预测，因为这种建模方法暴露了时空网络数据生成的基本方式。

此外，时空网络数据在空间和时间维度上都表现出异质性。例如，在城市范围内的道路网络中，住区和商业区的交通监测站记录的观测结果往往在不同的时间表现出不同的模式。然而，以往的研究大多采用不同时间段的共享模块，无法有效捕捉时空网络的异质性。

为了捕捉复杂的局部时空相关性和时空数据的异质性，我们提出了一个时空同步图卷积网络(STSGCN)模型。与以往的许多研究不同，STSGCN模型可以同时直接捕获局部时空相关性，而不是使用不同类型的深度神经网络分别对空间依赖性和时间相关性进行建模。具体来说，我们构建了局部时空图，将相邻时间步长的单个空间图连接成一个图。然后，我们构建了一个时空同步图卷积模块(STSGCM)来捕获这些局域时空图中复杂的局域时空相关性。同时，为了捕获远程时空网络数据的异质性，我们设计了一个时空同步图卷积层(STSGCL)，该层在不同的时间段部署了多个单独的stsgcm。最后，我们将多个STSGCLs叠加在一起，汇总长期时空相关性和异质性，用于预测。

总体而言，我们的工作贡献如下:

•我们提出了一种新的时空图卷积模块，可以直接同步捕获局部时空相关性，而不是单独使用不同类型的神经网络模块。

•我们构建了一个多模块层来捕获远程时空图中的异质性。这个多模块层在每个时间段上部署多个模块，允许每个模块专注于提取每个局部时空图上的时空相关性。

•在四个真实数据集上进行了广泛的实验，实验结果表明，我们的模型始终优于所有基线方法。

准备

定义1:空间网络G，用G = (V, E, A)表示空间网络，其中|V | = N为顶点集，N为顶点数，E为边集。A为网络G的邻接矩阵。空间网络G表示空间维度上节点之间的关系，网络结构不随时间变化。在我们的工作中，这个空间网络可以是有向的，也可以是无向的。

•定义2:图信号矩阵 $X_G^{(t)}\in R^{N \times C}$ ，其中C为属性特征个数，t为时间步长。此图信号矩阵表示时间步长t时空间网络G的观测值。

时空网络数据预测问题可以描述为:学习映射历史时空网络序列 $(X_G^{(t-T+1)},X_G^{(t-T+2)},...,X_G^{(t)})$ 来预测 $(X_G^{(t+1)},X_G^{(t+2)},...,X_G^{(t+{T}')})$ 的映射函数 $f$ ，其中 $T$ 为历史时空网络序列的长度， ${T}'$ 为待预测目标时空网络序列的长度。

时空同步图卷积网络

图2说明了我们的STSGCN模型的体系结构。我们将STSGCN的核心思想概括为三点:1)在前一步和下一步将每个节点与自身连接起来，构建局域化的时空图。2)使用时空同步图卷积模块捕获局部时空相关性。3)部署多个模块对时空网络序列的异构性进行建模。

图2:STSGCN架构。我们的STSGCN由多个具有输入层和输出层的时空同步图卷积层(stsgcl)组成。它使用输入层将输入特征转换为更高维度的空间。然后，叠加多个STSGCLs捕获时空网络序列中的局部时空相关性和异质性。最后，它使用多模块输出层将最终表示映射到输出空间。

局域时空图构建

我们打算建立一个模型，可以直接捕获每个节点对其邻居的影响，这些节点既属于当前时间步长，也属于相邻时间步长。实现这一目标的最直观的想法是在相邻的时间步将所有节点与其自身连接起来(图3 (a))。通过将所有节点与前一时刻和后一时刻的自身连接起来，我们可以得到一个局域化的时空图。根据局域化时空图的拓扑结构，可以直接捕获每个节点与其时空邻居之间的相关性。

图3:局域化时空图构建。(a)是一个局域化时空图的例子。(b)为(a)中局部时空图的邻接矩阵。 $A^{(t_i)}$ 表示时间步长i时空间图的邻接矩阵。 $A^{t_i \rightarrow t_j}$ 表示时间步长i和j时节点与自身的连接。

我们用 $A\in R^{N \times N}$ 表示空间图的邻接矩阵。 ${A}'\in R^{3N \times 3N}$ 表示在三个连续空间图上构造的局域时空图的邻接矩阵。对于空间图中的节点 $i$ ，我们可以计算其在局部时空中的新索引图 $(t-1)N+i$ ，其中t (0 < t≤3)表示局域化时空图中的时间步长。如果在这个局域化的时空图中有两个节点相互连接，则邻接矩阵中对应的值设为1。局域化时空图的邻接矩阵可表示为:

式中， $v_i$ 为局域时空图中的节点 $i$ 。邻接矩阵 ${A}'$ 包含3N个节点。图3 (b)给出了局域化时空图的邻接矩阵。邻接矩阵的对角线是三个连续时间步长的空间网络的邻接矩阵。对角线的两边表示属于相邻时间步长的每个节点与自身的连通性。

时空嵌入

然而，将不同时间步长的节点连接到一个图中会模糊每个节点的时间属性。换句话说，这个局域化的时空图将不同时间步长的节点放在同一个环境中，而不区分它们。受ConvS2S启发(Gehring等2017)，我们将位置嵌入到时空网络序列中，使模型能够考虑时空信息，从而增强了对时空相关性的建模能力。对于时空网络序列 $X_G \in R^{N \times C \times T}$ ，我们创建一个可学习的时间嵌入矩阵 $T_{emb} \in R^{ C \times T}$ 和可学习空间嵌入矩阵 $S_{emb} \in R^{ N \times C}$ 。训练过程完成后，两个嵌入矩阵将包含必要的时间和空间信息，以帮助模型捕获时空相关性。

我们将这两个嵌入矩阵通过广播运算加入到时空网络序列中，得到网络序列的新表示: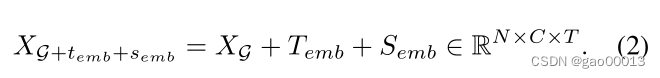

时空同步图卷积模块

我们构建了一个时空同步图卷积模块(STSGCM)来捕获局部时空相关性。STSGCM由一组图卷积操作组成。图卷积运算可以将每个节点的特征与其相邻节点进行聚合。我们在顶点域中定义了一种图卷积运算来聚合时空网络中的局域时空特征。图卷积运算的输入是局域化时空图的图信号矩阵。在我们的图卷积操作中，每个节点在相邻的时间步长上聚合自己和邻居的特征。聚合函数是一个线性组合，其权值等于节点与其相邻节点之间的边的权值。然后，我们部署一个带有激活函数的全连接层，将节点的特征转化为一个新的空间。该图卷积运算可表示为:

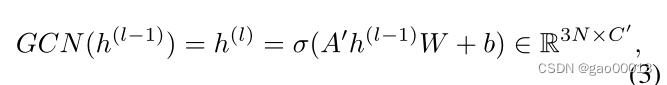
其中 ${A}'\in R^{3N \times 3N}$ 表示局域化时空图的邻接矩阵， $h^{(l-1)}\in R^{3N \times C}$ 表示第 $l$ 个图卷积层的输入， $W\in R^{C \times {C}'}$ 和 $b\in R^{C'}$ 为可学习参数，σ表示激活函数，如ReLU和GLU (Dauphin et al 2017)。如果我们选择GLU作为图卷积层的激活函数，则图卷积层可以描述为:

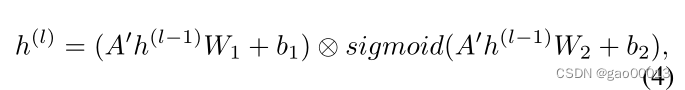
其中， $W_1\in R^{C \times {C}'}$ , $W_2\in R^{C \times {C}'}$ , $b_1\in R^{C'}$ , $b_2\in R^{C'}$ 为可学习参数，sigmoid表示sigmoid激活函数，即sigmoid(x) = $\frac{1}{1+e^{-x}}$ ，⊗表示元素智能积。门控线性单元控制哪个节点的信息可以传递到下一层。

这个图卷积运算是在顶点域中定义的，这意味着它不需要计算图拉普拉斯向量。此外，这种图卷积运算不仅可以应用于无向图，也可以应用于有向图。此外，我们在局域化时空图的每个节点上添加了自循环，以便图卷积运算在聚合特征时考虑到自身的特征。

我们叠加多个图卷积操作来扩展聚集区域，这可以增加图卷积操作的接受域，以捕获局部时空相关性(图4 (a))。我们选择JK-net (Xu et al . 2018)作为STSGCM的基础结构，并设计了一个新的聚合层来过滤无用信息(图4 (b)， 4 (c))。

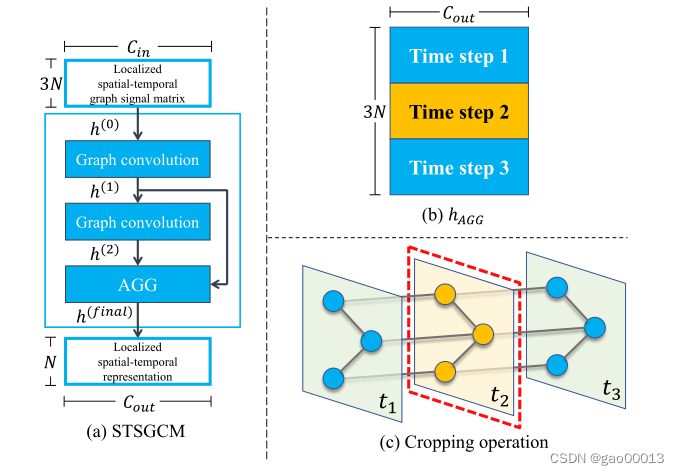
图4:(a)是具有两个图卷积操作的时空同步图卷积模块的架构示例。 $C_{in}$ 和 $C_{out}$ 分别表示输入矩阵和输出矩阵的特征个数，AGG表示聚合层。(b)表示聚合操作的输出。(c)为聚合层裁剪操作示例，仅保留中间时间步的节点

我们用 $h^{(l)}$ 表示第 $l$ 个图卷积运算的输出，其中 $h^{(0)}$ 表示第一个图卷积运算的输入。对于具有L个图卷积操作的STSGCM，每个图卷积操作的输出将被馈送到聚合层(图4 (a))。聚合层将压缩STSGCM中所有层的输出。聚合操作有两个步骤:聚合和裁剪。

聚合操作

我们选择最大池作为聚合操作。它对STSGCM中所有图形卷积的输出应用一个元素max操作。max操作需要所有的输出都有相同的大小，所以一个模块内图形卷积操作的核数应该是相等的。最大聚合操作可表示为:

其中Cout表示图卷积运算的核数。

裁剪操作

裁剪操作(图4 (c))删除了节点在前一个和下一个时间步长的所有特征，只保留中间时刻的节点。原因是图卷积运算已经聚合了前一个和下一个时间步的信息。即使我们裁剪了两个时间步，每个节点也包含了局部的时空相关性。如果将多个stsgcm叠加在一起并保留所有相邻时间步长的特征，会导致模型中存在大量冗余信息，严重影响模型的性能。

综上所述，STSGCM的输入是一个局域时空图信号矩阵 $h^{(0)}\in R^{3N \times C_{in}}$ 。经过多次图卷积运算后，每次图卷积运算的输出可记为 $h^{(i)}\in R^{3N \times C_{out}}$ ，其中 $i$ 为运算指标。聚合操作将它们压缩成 $h_{AGG}\in R^{3N \times C_{out}}$ 。然后裁剪操作保留中间时间步的节点，生成 $STSGCMh^{(final)}\in R^{N \times C_{out}}$ 的输出。图1中的绿色箭头表示在局部时空图中节点与其两跳邻居之间的时空相关性。具有至少两个堆叠图卷积操作的stsgcm可以直接对图1中所示的三种不同类型的相关性进行建模。

时空同步图卷积层

为了捕捉整个网络序列的长期时空相关性，我们使用滑动窗口来剪切不同的时间段。由于时空数据的异质性，最好使用多个stsgcm来模拟不同时期，而不是所有时期共享一个。多个stsgcm允许每个stsgcm专注于建模局域图中的局域时空相关性。我们部署了一组stsgcm作为时空同步图卷积层(STSGCL)来提取远程时空特征，如图2所示。

我们将STSGCL的输入矩阵记为 $X\in R^{T \times N \times C}$ 。我们首先为每个STSGCL添加时空嵌入。然后STSGCL中的滑动窗口将输入截断到T−2时空网络序列中。每个时空网络序列可表示为 $X'\in R^{3\times N \times C}$ 。我们将其重塑为 $X'_{reshape}\in R^{3N \times C}$ ，可以直接将其与局部时空图一起馈入STSGCM。STSGCL在T−2局域时空图上部署T−2 stsgcm，以捕获这些T−2时空网络序列中的局域时空相关性。然后，将所有这些T−2 stsgcm的输出串联成一个矩阵，作为STSGCL的输出。可以表示为:，其中 $M_i \in R^{N \times C_{out}}$ 表示第 $i$ 个STSGCM的输出。

通过叠加多个stsgcl，我们可以建立一个能够捕获复杂时空相关性和时空异质性的分层模型。经过多次时空同步图卷积运算后，每个节点将包含以自身为中心的局域时空关联。

额外的组件

在本节中，我们将介绍STSGCN为增强其表示能力而配备的一些额外组件。

掩模矩阵

对于STSGCN中的图卷积操作，邻接矩阵A'决定聚合权值。然而，每个节点对其邻居的影响程度不同。如果邻接矩阵只包含0和1，则可能限制聚合。如果局域化时空图中的两个节点是连通的，即使它们在某一时期没有相关性，它们的特征也会被聚合。因此，我们在STSGCN中加入一个可学习的掩码矩阵 $W_{mask}$ 来调整聚合权值，使聚合更加合理。

$W_{mask} \in R^{3N \times 3N}$ 表示掩码矩阵。我们 $W_{mask}$ 和局部邻接矩阵A'之间做元素积，生成一个权值调整后的局部邻接矩阵:

之后，我们使用 $A'_{adjusted}$ 来计算我们模型中的所有图卷积。

输入层

我们在网络的顶部增加了一个全连接层，将输入转换成一个高维空间，这样可以提高网络的表示能力。

输出层

我们设计了一个输出层，将最后一个STSGCL的输出转换为预期的预测。该输出层的输入可以表示为 $X \in R^{T\times N \times C}$ 。我们首先将其转置并重塑为 $X^T \in R^{N \times TC}$ ，然后使用 $T'$ 两个完全连通层生成如下预测:

其中， $\hat{y}^{(i)}$ 表示时间步长 $i$ 的预测。 $W_1^{(i)} \in R^{TC \times C'},b_1^{(i)} \in R^{C'},W_2^{(i)} \in R^{C' \times 1},b_2^{(i)} \in R$ 是可学习的参数，C'表示第一个全连接层的输出特征的个数。然后我们将每个时间步的所有预测连接到一个矩阵中:

其中 $\hat{Y}$ 是整个STSGCN的输出。

损失函数

我们选择Huber loss (Huber 1992)作为损失函数。与误差平方损失相比，Huber损失对异常值的敏感性较低。

其中，Y表示真实值， $\hat{Y}$ 表示模型预测值，δ是控制误差损失平方范围的阈值参数

实验

我们在四个高速公路交通数据集上评估了STSGCN的性能。这些数据收集自Caltrans绩效测量系统(PeMS) (Chen et al . 2001)。

数据集

我们分别从4个地区构建了4个不同的数据集，分别是PEMS03、PEMS04、PEMS07和PEMS08。

流量数据汇总为5分钟，即每小时流量数据中有12个点。我们使用过去一小时的交通流量数据来预测下一小时的交通流量。详细信息见表1。

每个数据集的空间网络是根据实际道路网络构建的。如果两个监视器在同一条道路上，则认为这两个点在空间网络中是连通的。我们通过去除平均值和缩放到单位方差来标准化特征:

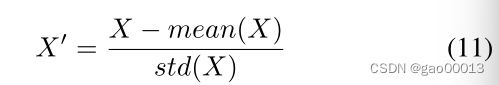
其中mean(X)和std(X)分别为历史时间序列的均值和标准差。

基准模型

•V AR (Hamilton 1994): V向量自回归是一种先进的时间序列模型，可以捕捉时间序列之间的两两关系。

•SVR (Drucker et al . 1997):支持V向量回归使用线性支持向量机进行回归任务。

•LSTM (Hochreiter and Schmidhuber 1997):用于时间序列预测的长短期记忆网络。

•DCRNN (Li et al 2017): Diffusion Convolutional Recurrent Neural Network利用扩散图卷积网络和seq2seq分别对空间信息和时间信息进行编码。

•STGCN (Y u, Yin, and Zhu 2018):时空图卷积网络。STGCN分别使用ChebNet和2D卷积网络来捕获空间依赖性和时间相关性。

•ASTGCN(r) (Guo et al . 2019a):基于注意力的时空图卷积网络(Attention Based SpatialTemporal Graph Convolutional Networks)分别设计空间注意力和时间注意力机制来模拟空间和时间动态。ASTGCN集成了三个不同的组件来模拟公路交通数据的周期性。为了保证比较实验的公正性，我们只取其最近的分量。

•STG2Seq (Bai et al . 2019):时空图到序列模型(Spatial-Temporal Graph to Sequence Model)使用多门控图卷积模块和带有注意机制的seq2seq架构进行多步预测。

•Graph WaveNet (Wu et al . 2019): Graph WaveNet将图卷积与扩展随机卷积相结合，以捕获时空依赖关系。

实验设置

我们将所有比例为6:2:2的数据集分成训练集、验证集和测试集。我们用一个小时的历史数据来预测下一个小时的数据，这意味着用过去的12个连续时间步来预测未来的12个连续时间步。所有的实验都要重复十次。

我们使用MXNet实现STSGCN模型(Chen et al . 2015)。超参数由模型在验证数据集上的性能决定。这四个数据集上的最佳模型由4个STSGCM组成，每个STSGCM分别包含3个图卷积运算，分别包含64、64、64个滤波器。

实验结果

表2显示了预测任务的不同方法的比较。除了PEMS07之外，我们的STSGCN在三个数据集上始终优于其他基线方法。在PEMS07中，除了RMSE略大于DCRNN外，我们的STSGCN具有最好的MAE和MAPE。

var、SVM和LSTM只考虑时间相关性，不能利用时空网络的空间依赖性。DCRNN、STGCN、ASTGCN(r)、STG2Seq和我们的STSGCN都利用了空间信息，因此它们比仅用于时间序列预测的方法具有更好的性能。

DCRNN、STGCN、ASTGCN和Graph WaveNet分别使用两个模块对空间依赖性和时间相关性进行建模。他们和所有人共用一个模块在不同时段提取长程时空相关性，忽略了时空网络数据的异质性。我们的方法考虑了局部时空相关性，并捕获了时空数据的异质性，因此我们的STSGCN比这些方法具有更好的性能。

STG2Seq还打算同时对时空相关性进行建模。从表2中可以看出，我们的STSGCN在这四个数据集上具有更好的性能。STG2Seq的局限性在于它只是简单地将相邻周期的特征连接起来，而不是像我们的STSGCN那样将不同时间步长的节点视为不同的单个节点。在某种程度上，这种方法忽略了时间信息和时空相关性。

成分分析

为了进一步研究STSGCN不同模块的效果，我们设计了6种不同的STSGCN模型。我们将这六种变体与PEMS03数据集上的STSGCN模型进行了比较。所有这些模型都包含四个stsgcl，每个STSGCM中都有[64,64,64]个过滤器。

这七种模型的区别如下:

1.basic:该模型不具备时空嵌入和掩模矩阵。它使用ReLU作为激活函数。每个STSGCL只包含一个STSGCM，并且在所有时间段共享该模块。输出层与ASTGCN的输出层相同，后者只是使用带有12个过滤器的卷积层来生成预测。

2. 多模块:该模型将基础模型中的stsgcl改为多模块版本。

3.GLU:该模型将多模块模型中的所有激活函数都改为GLU。

4. +emb:该模型基于GLU版本在每个STSGCL中添加时空嵌入。

5. +mask:该模型基于+emb添加掩码矩阵。

6. shape-output:该模型使用两个完全连接的层来生成预期的预测。

7. STSGCN: STSGCN模型部署多个两个完全连接的层来生成每个时间步长的预测。

如图5所示，GLU具有比ReLU激活函数更好的性能。原因是GLU的参数大小是ReLU的两倍，因此其更大的容量使其能够捕获复杂的时空相关性。

此外，它可以比ReLU更灵活地控制输出。每个时间段配备单独的STSGCM的模型的性能明显优于共享的STSGCM，这表明了对时空网络数据异构性建模的必要性。

此外，结果表明，时空嵌入可以明显提高STSGCN模型的性能。我们添加掩码矩阵来调整图卷积操作中每个节点与其相邻节点之间的权重。该方法对预测性能有一定的提高。

用于生成预测的卷积层没有意义，因为它与空间图中的所有节点共享所有参数。由于时空数据的异质性，每个节点可能表现出不同的属性，因此使用不同的模块来生成预测结果比使用一个卷积输出层更好。因此，重塑的输出层和多输出版本可以进一步提高预测性能。

结论

我们提出了一个既能有效捕捉局部时空相关性又能考虑到时空数据异质性的模型。在四个实际数据集上的大量实验表明，我们的模型优于现有的模型。此外，该模型是一个时空网络数据预测的通用框架，因此可以应用于许多相关应用。代码和数据集已在https://github.com/Davidham3/STSGCN上发布。