首先,我们举个例子来说明什么是生成学习算法:
假设要判定一个病人所患的是癌症是良性的还是恶性的,我们可以分别对恶性的样本进行训练得到一个模型,再在对良性的样本进行
训练得到一个模型,然后对新的病人分别匹配这两个样本看看哪一个样本匹配的更好,匹配较好的那个即为所求。
生成学习算法概念:对两个类别的样本分别进行建模,用新的样本去匹配两个模型,匹配度较高的作为新样本的类别。
判别算法的概念:之前我们所说的分类算法称之为判别算法,他通过学习p(y|x)或
感知机算法是都是判别算法的一个实例。也就是说判别算法是在解空间中寻求一条直线从而把两种类别的样本分开,对于新的样本只
要判断他属于直线那一侧就可以了。
生成学习算法和判别算法形式化定义的差别:
1) 判别学习算法:直接学习p(y|x),即给定输入特征,输出所属的类;或者学习得到一个(x),直接输出0或者和1.
2) 生成学习算法:对p(x|y)进行建模,p(x|y)表示在给定所属的类的情况下,显示某种特征的概率。处于技术上的考虑,他也会对p(y)
进行建模。
以上述癌症的例子为例:p(x|y)(条件概率)可以看成假定一个癌症为恶性或良性,生成学习会对该条件下的癌症的症状x的概率分
布进行建模,并且对p(y)先验概率进行建模,则我们根据贝叶斯公式可以求出后验概率:
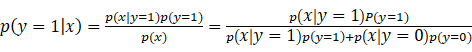
高斯判别算法(GDA):注意高斯判别算法不是判别算法,而是生成算法,不要被他的名字所误导。在GDA中,我们假设p(x|y)满足高斯
分布。这里我们回顾下
高斯分布:
高斯分布,也被成为正态分布,广泛应用于连续型随机变量分布的模型中。一元高斯分布我们在之前的章节中已经做过介绍,这里介
绍一个多元高斯分布,假设x是n维向量 ,则其多元高斯分布的概率密度函数为:
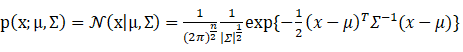 (2)
(2)
其中,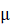
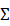
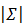
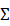
注意根据协方差矩阵的定义: 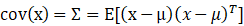
其数学期望为: 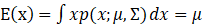
现在我们正式开始关于GDA算法的介绍,这个模型所针对的变量是连续的,这个模型的标签y服从伯努利分布,即
条件概率满足p(x|y)服从高斯分布(正太分布),则有以下分布律:
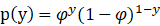
并且有:
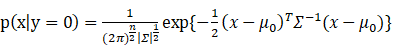 (6)
(6)
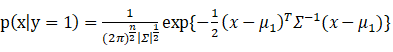 (7)
(7)
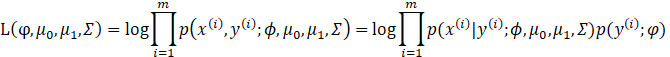 (8)
(8)
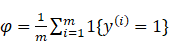 (9)
(9)
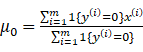 (10)
(10)
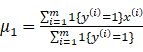 (11)
(11)
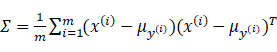 (12)
(12)
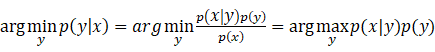 (13)
(13)
因为p(x)独立于y,所以可以忽略p(x).若取每种类型的概率都相同,即p(y=0)=p(y=1),那么求解过程变成:
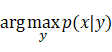
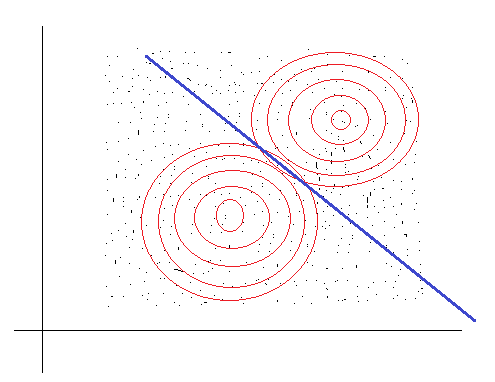
接下来我们将用一张图来说明高斯判别法的分类过程:
说明:我们先根据正样本,也就是x只观察正样本,之后拟合出一个正样本数据的高斯分布p(x|y=1),如图蓝色直线的左下方就是所求的
正样本对应的高斯分布图,同理我们会根据负样本继续拟合出一个高斯p(x|y=0),图中蓝色直线右上方即为所求,这样我们就得到了两个分
类器。注意这两个分类器有不同的均值,但是有用相同的协方差矩阵。
GDA与logistic之间的关系
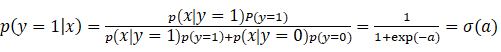
由(15)可得
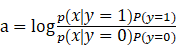
所以我们说,GDA的后验分布可以表示成logistic分布。
接下来我们通过图像来举例说明两者之间的关系:
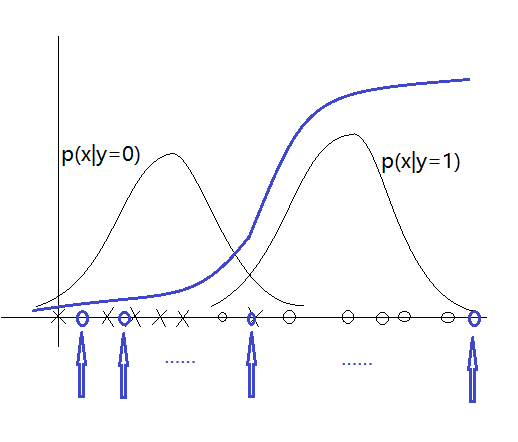
如图,假设我们有一个训练集合,包含一些负样本和一些正样本,假如我们运行了高斯判别分析,之后我们对每一类样本拟合出
一个概率密度函数,对于这2类中的每一类都会拟合出一个高斯概率密度函数,现在我们沿着x轴进行变化,对于水平x轴上的x我
们画出p(y=1|x),我们根据以下式子来计算p(y=1|x).
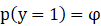 (18)
(18)
根据上述2个式子,我们可以计算出每个x对应p(y=1|x),我们将p(y=1|x)画出来就会得到一条形状类似于logistic的回归中用到sigmoid
函数曲线。换句话说,当你做出假设,使用高斯分布,当你回归计算p(y|x)时,实际上几乎得到了之前和我们在logistic回归中使用的
sigmoid函数一样的函数。注意实际上高斯判别分析得到的曲线,无论是位置还是陡峭程度都和logistic回归中的sigmoid函数不同。
综上所述:我们从推导过程中知道,logistic回归是生成学习模型的特例,假设x|y~Gaussian分布,则他的后验概率p(y=1|x)将是一
个logistic分布。但是事实证明这是个充分不必要条件,同时我们可以得出:指数族分布和高斯判别分析都能推导出logistic模型。
那么竟然是这样,你该如何在高斯判别分析于logistic回归之间进行权衡呢?
首先,高斯判别分析做了一个更强的假设,即x|y~Gaussian。所以当这个假设正确或者接近正确时,也就是说当你在画点时,x|y大
概服从高斯分布时,此时如果你在算法中显示地作出这个假设,那么这个高斯判别分析算法的表现将更好,因为这个算法利用了更多关于
数据的信息,算法知道数据服从高斯分布,所以如果高斯假设成立或者大概成立,那么高斯判别分析将会优于logistic回归。相反,如果你
不确定x|y的分布情况,那么logistic回归将会是个更加值得选择的算法,因为它做出了更少的假设,构建的模型更加健壮。y事实证明高斯
判别算法需要的更少的数据即更少的样本,因为他假设样本服从高斯分布已经默认地知道了更多关于数据的信息,而logistic回归的假设更
少,对模型的假设更为健壮,因为你做了更弱的假设,但你可能需要更多的样本。
朴素贝叶斯算法
我们在此引入垃圾邮件分类器的例子,假设你要实现一个垃圾邮件分类器,以邮件的输入流作为输入,确定邮件是否为垃圾邮件。
使用标签y={0,1},其中1表示垃圾邮件,0表示非垃圾邮件。我们要做的是给你一封邮件,你要怎样用表示这篇邮件,邮件仅仅是一段文本
,就像一个词列表,所以我可以将电子邮件表示为一个特征向量x,我们可以有多种不同的表示方法,我们这里使用的是向量空间模型,也
就是说我们利用已经存在的词典,该词典可以是从样本中统计出来的,例如词典可以是过去3个月中出现3次以上的词,对于每个邮件,我们
用长度等于词典大小的向量表示,如果邮件中包含某个词,则这个词在词典中的索引index设置成1,否则设置成0,如面式子所示:
现在假设我们的词典中有50000个词,即向量x的长度为50000,其每个元素的取值为{0,1},那么显然这是一个多项式分布,我们要对种可能
进行建模,说需要的参数为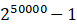
在朴素贝叶斯算法中,我们会对p(x|y)做一个非常强的假设,即在给定y的时候,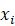
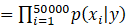
这个式子的意思是:文本中(邮件中)出现某个词语时不会影其他词语在文本中出现的概率。
我们对朴素贝叶斯算法所涉及到的参数做如下假设:
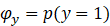
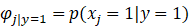
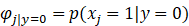
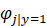
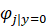
于是我们可以得到朴素贝叶斯算法中的极大似然估计算法:
注意这里我们的y的曲子是0或者1,我们说他满足伯努利分布。
我们利用极大似然极大算法得:
m表示样本数量,就是邮件数量,训练样本可以是过去2个月中收到的所有邮件,并将他们标为垃圾和非垃圾。
拉普拉斯平滑
我们所叙述的贝叶斯算法存在明显的缺陷,当你遇到一个新的词语时你该怎么办呢?假设有一个单词在你的词库中一直有这个单词,
但是对于你的邮件(无论是垃圾邮件,还是非垃圾邮件)之前都没出现过这个单词。我们假设这个单词在词典中的索引index=30000.
那么我们可以得到下面的式子:
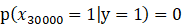
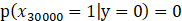
所以当你的垃圾邮件分类器开始计算p(y=1|x)时,有:
其中:
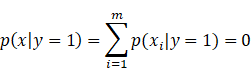
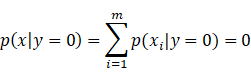
上面是式子等于0,是由(27),(28)得到的。
所以
很显然(27),(28)不是一个很好的假设。
这里我们引入拉普拉斯平滑,这里我们引入一个不是很恰当例子,假设周一到周六都是阴天,那么你判定周日晴天的概率是多少呢?
我们不能因为前面6天是阴天就断定周日也是阴天,正常情况下我们应该这么做。假设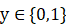
这种方法被成为拉普拉斯平滑。
跟一般的情况,假设y满足多项式分布,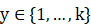
所以对于我们的贝叶斯算法,有
所以我们的朴素贝叶斯算法大体思路如下:
1)
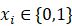 所以我们的朴素贝叶斯算法大体思路如下:
所以我们的朴素贝叶斯算法大体思路如下:
2)计算:








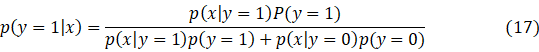
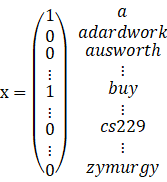
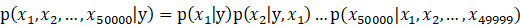
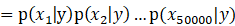
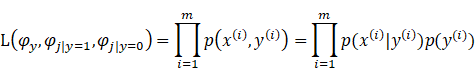
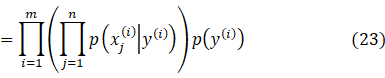
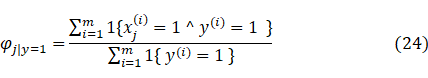
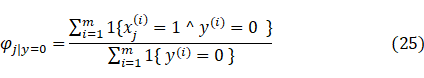

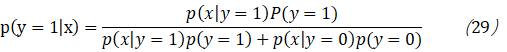
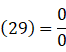
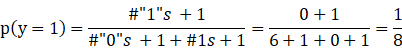
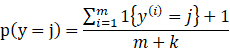
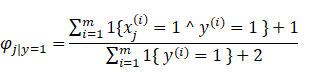
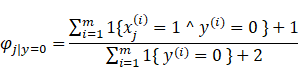
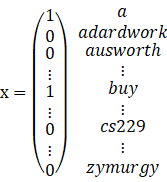
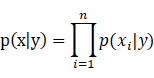
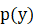
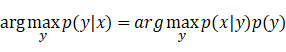














 2308
2308

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








