Conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive definite. The conjugate gradient method is an iterative method, so it can be applied to sparsesystems which are too large to be handled by direct methods such as the Cholesky decomposition. Such systems arise regularly when numerically solving partial differential equations.
The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization.
The biconjugate gradient method provides a generalization to non-symmetric matrices. Variousnonlinear conjugate gradient methods seek minima of nonlinear equations.
Description of the method
Suppose we want to solve the following system of linear equations
- Ax = b
where the n-by-n matrix A is symmetric (i.e., AT = A), positive definite (i.e., xTAx > 0 for all non-zero vectors x in Rn), and real.
We denote the unique solution of this system by x*.
The conjugate gradient method as a direct method
We say that two non-zero vectors u and v are conjugate (with respect to A) if
Since A is symmetric and positive definite, the left-hand side defines an inner product
So, two vectors are conjugate if they are orthogonal with respect to this inner product. Being conjugate is a symmetric relation: if u is conjugate to v, then v is conjugate to u. (Note: This notion of conjugate is not related to the notion of complex conjugate.)
Suppose that {pk} is a sequence of n mutually conjugate directions. Then the pk form a basis ofRn, so we can expand the solution x* of Ax = b in this basis:
The coefficients are given by
This result is perhaps most transparent by considering the inner product defined above.
This gives the following method for solving the equation Ax = b. We first find a sequence of nconjugate directions and then we compute the coefficients αk.
The conjugate gradient method as an iterative method
If we choose the conjugate vectors pk carefully, then we may not need all of them to obtain a good approximation to the solution x*. So, we want to regard the conjugate gradient method as an iterative method. This also allows us to solve systems where n is so large that the direct method would take too much time.
We denote the initial guess for x* by x0. We can assume without loss of generality that x0 = 0 (otherwise, consider the system Az = b − Ax0 instead). Note that the solution x* is also the unique minimizer of the quadratic form
This suggests taking the first basis vector p1 to be the gradient of f at x = x0, which equalsAx0−b or, since x0 = 0, −b. The other vectors in the basis will be conjugate to the gradient, hence the name conjugate gradient method.
Let rk be the residual at the kth step:
Note that rk is the negative gradient of f at x = xk, so the gradient descent method would be to move in the direction rk. Here, we insist that the directions pk are conjugate to each other, so we take the direction closest to the gradient rk under the conjugacy constraint. This gives the following expression:
(see the picture at the top of the article for the effect of the conjugacy constraint on convergence).
The resulting algorithm
After some simplifications, this results in the following algorithm for solving Ax = b where A is a real, symmetric, positive-definite matrix. The input vector x0 can be an approximate initial solution or 0.
-

-
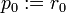
-

-
repeat
-
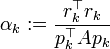
-

-

- if r k+1 is "sufficiently small" then exit loop end if
-

-

-

-
- end repeat
-
The result is

Example of conjugate gradient method for Octave
function [x] = conjgrad(A,b,x0) r = b - A*x0; w = -r; z = A*w; a = (r'*w)/(w'*z); x = x0 + a*w; B = 0; for i = 1:size(A)(1);r = r - a*z; if( norm(r) < 1e-10 ) break; endif B = (r'*z)/(w'*z); w = -r + B*w; z = A*w; a = (r'*w)/(w'*z); x = x + a*w; end end
Preconditioner
A preconditioner is a matrix P such that P-1A has a smaller condition number (κ) than A and so solving P-1Ax=P-1b is faster than solving Ax=b (see preconditioned conjugate gradient method).
Conjugate gradient on the normal equations
The conjugate gradient method can be applied to an arbitrary n-by-m matrix by applying it tonormal equations ATA and right-hand side vector ATb, since ATA is a symmetric positive (semi-)definite matrix for any A. The result is conjugate gradient on the normal equations (CGNR).
- A T Ax = A T b
As an iterative method, it is not necessary to form ATA explicitly in memory but only to perform the matrix-vector and transpose matrix-vector multiplications. Therefore CGNR is particularly useful when A is a sparse matrix since these operations are usually extremely efficient. However the downside of forming the normal equations is that the condition number κ(ATA) is equal to κA2and so the rate of convergence of CGNR may be slow. Finding a good preconditioner is often an important part of using the CGNR method.
Several algorithms have been proposed (e.g., CGLS, LSQR). The LSQR algorithm purportedly has the best numerical stability when A is ill-conditioned, i.e., A has a large condition number.
See also
- Biconjugate gradient method (BICG)
- Preconditioned conjugate gradient method (PCG)
- Nonlinear conjugate gradient method
References
The conjugate gradient method was originally proposed in
- Hestenes, Magnus R.; Stiefel, Eduard (December, 1952). "Methods of Conjugate Gradients for Solving Linear Systems". Journal of Research of the National Bureau of Standards 49 (6),http://nvl.nist.gov/pub/nistpubs/jres/049/6/V49.N06.A08.pdf.
Descriptions of the method can be found in the following text books:
- Kendell A. Atkinson (1988), An introduction to numerical analysis (2nd ed.), Section 8.9, John Wiley and Sons. ISBN 0-471-50023-2.
- Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- Gene H. Golub and Charles F. Van Loan, Matrix computations (3rd ed.), Chapter 10, Johns Hopkins University Press. ISBN 0-8018-5414-8.
External links
- Conjugate Gradient Method by Nadir Soualem.
- Preconditioned conjugate gradient method by Nadir Soualem.
- An Introduction to the Conjugate Gradient Method Without the Agonizing Pain by Jonathan Richard Shewchuk.
- Iterative methods for sparse linear systems by Yousef Saad
- LSQR: Sparse Equations and Least Squares by Christopher Paige and Michael Saunders.











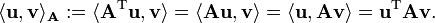


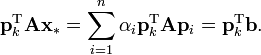
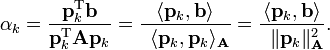
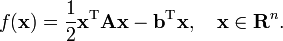
















 3391
3391











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








