思考
首先让我们来思考一个问题,给定一个数组,和left与right的值,让你求这个数组中left到right之间元素的和,你会怎么计算?最简单的当然是遍历。如果有人问你这个问题的时候,他决对是会让你优化的,起码时间复杂度一定要小于O(n),那你打算怎么做呢?
很明确的一点是,如果要优化时间复杂度,就必须要提高空间复杂度,这是算法的局限,当然也是自然界的能量守恒定律。这是不可避免的,
所以接下来你可以思考下,有什么结构可以实现了。
分块处理
这种就真的很基础了,就是开辟一个额外的数组来存储区间和。
设数组大小为 n,我们将数组 nums分成多个块,每个块大小 size,最后一个块的大小为剩余的不超过 size 的元素数目,那么块的总数为 n/size,用一个数组 sum 保存每个块的元素和。
那么究竟要分成多少个数组,才能在数量和速度上都是最优解那? 这个关键在于size的取值。在求和时:设left位于b1个块内的第i1个元素,right位于b2个块内的第i2个元素。如果b1=b2,那么直接返回第b1个块位于区间[i1,i2]的元素的和;否则计算第b1个块位于区间[i,size)的元素之和sum1,第b2个块位于区间[0,i2]的元素之和sum2,第b1+1个块到第b2-1个块的元素的总和sum3,返回sum1+sum2+sum3。这个求和的时间复杂度为。因为
,当且仅当
时等号成立。因此size的取值为
。此时的时间复杂度为
var NumArray = function(nums) {
this.nums = nums;
const n = nums.length;
size = Math.floor(Math.sqrt(n));
this.sum = new Array(Math.floor((n + size - 1) / size)).fill(0); // n/size 向上取整
for (let i = 0; i < n; i++) {
this.sum[Math.floor(i / size)] += nums[i];
}
};
NumArray.prototype.update = function(index, val) {
this.sum[Math.floor(index / size)] += val - this.nums[index];
this.nums[index] = val;
};
NumArray.prototype.sumRange = function(left, right) {
const b1 = Math.floor(left / size), i1 = left % size, b2 = Math.floor(right / size), i2 = right % size;
if (b1 === b2) { // 区间 [left, right] 在同一块中
let sum = 0;
for (let j = i1; j <= i2; j++) {
sum += this.nums[b1 * size + j];
}
return sum;
}
let sum1 = 0;
for (let j = i1; j < size; j++) {
sum1 += this.nums[b1 * size + j];
}
let sum2 = 0;
for (let j = 0; j <= i2; j++) {
sum2 += this.nums[b2 * size + j];
}
let sum3 = 0;
for (let j = b1 + 1; j < b2; j++) {
sum3 += this.sum[j];
}
return sum1 + sum2 + sum3;
};
线段树
线段树是一种二叉树,也就是对于一个线段,我们会用一个二叉树来表示。比如说一个长度为4的线段,我们可以表示成这样:

这是什么意思呢? 如果你要表示线段的和,那么最上面的根节点的权值表示的是这个线段 1 ∼ 4 的和。根的两个儿子分别表示这个线段中 1 ∼ 2 的和,与 3 ∼ 4 的和。以此类推。
然后我们还可以的到一个性质:节点 i 的权值 = 她的左儿子权值 + 她的右儿子权值。因为 1 ∼ 4 的和就是等于 1 ∼ 2 的和与 2 ∼ 3 的和的和。
给定区间 [left,right]时,我们将区间 [left,right] 拆成多个结点对应的区间。
- 如果结点 node 对应的区间与 [left,right] 相同,可以直接返回该结点的值,即当前区间和。
- 如果结点 node 对应的区间与 [left,right]不同,设左子结点对应的区间的右端点为 m,那么将区间 [left,right] 沿点 m拆成两个区间,分别计算左子结点和右子结点。
我们从根结点开始递归地拆分区间 [left,right]。
var NumArray = function(nums) {
n = nums.length;
this.segmentTree = new Array(nums.length * 4).fill(0);
this.build(0, 0, n - 1, nums);
};
NumArray.prototype.update = function(index, val) {
this.change(index, val, 0, 0, n - 1);
};
NumArray.prototype.sumRange = function(left, right) {
return this.range(left, right, 0, 0, n - 1);
};
NumArray.prototype.build = function(node, s, e, nums) {
if (s === e) {
this.segmentTree[node] = nums[s];
return;
}
const m = s + Math.floor((e - s) / 2);
this.build(node * 2 + 1, s, m, nums);
this.build(node * 2 + 2, m + 1, e, nums);
this.segmentTree[node] = this.segmentTree[node * 2 + 1] + this.segmentTree[node * 2 + 2];
}
NumArray.prototype.change = function(index, val, node, s, e) {
if (s === e) {
this.segmentTree[node] = val;
return;
}
const m = s + Math.floor((e - s) / 2);
if (index <= m) {
this.change(index, val, node * 2 + 1, s, m);
} else {
this.change(index, val, node * 2 + 2, m + 1, e);
}
this.segmentTree[node] = this.segmentTree[node * 2 + 1] + this.segmentTree[node * 2 + 2];
}
NumArray.prototype.range = function(left, right, node, s, e) {
if (left === s && right === e) {
return this.segmentTree[node];
}
const m = s + Math.floor((e - s) / 2);
if (right <= m) {
return this.range(left, right, node * 2 + 1, s, m);
} else if (left > m) {
return this.range(left, right, node * 2 + 2, m + 1, e);
} else {
return this.range(left, m, node * 2 + 1, s, m) + this.range(m + 1, right, node * 2 + 2, m + 1, e);
}
}
树状数组
树状数组是一种可以动态维护序列前缀和的数据结构(序列下标从 1 开始)
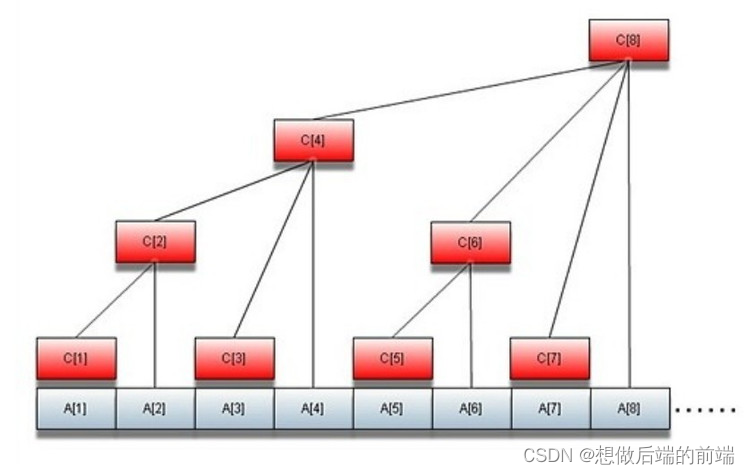
如图,A是基本数组,C是求和数组,
其中,C[1]=A[1], C[2]=C[1]+A[2], C[3]=A[3], C[4]=C[2]+C[3]+A[4]......C[8]=C[4]+C[6]+C[7]+A[8]......
树状数组最简单最经典的使用场景,就是单点更新区间查询:
- 单点修改 add(index,val):把序列第 index 个数增加 val;
- 区间查询 prefixSum(index):查询前 index个元素的前缀和。
前置知识—lowbit(x)运算
如何计算一个非负整数n在二进制下的最低为1及其后面的0构成的数?
例如:44 的二进制表示为 (101100),最低为1和后面的0构成的数是( 100 ) 是 4 。44的二进制=(101100),我们对44的二进制数取反+1,也即~44+1,得到-44
-44的二进制=(010100),然后我们把44和-44的二进制进行按位与运算,也即按位&得到,二进制000100,也就是十进制的4
所以lowbit(x) = x&(-x)
var NumArray = function(nums) {
this.tree = new Array(nums.length + 1).fill(0);
this.nums = nums;
for (let i = 0; i < nums.length; i++) {
this.add(i + 1, nums[i]);
}
};
NumArray.prototype.update = function(index, val) {
this.add(index + 1, val - this.nums[index]);
this.nums[index] = val;
};
NumArray.prototype.sumRange = function(left, right) {
return this.prefixSum(right + 1) - this.prefixSum(left);
};
NumArray.prototype.lowBit = function(x) {
return x & -x;
}
NumArray.prototype.add = function(index, val) {
while (index < this.tree.length) {
this.tree[index] += val;
index += this.lowBit(index);
}
}
NumArray.prototype.prefixSum = function(index) {
let sum = 0;
while (index > 0) {
sum += this.tree[index];
index -= this.lowBit(index);
}
return sum;
}
树状数组和线段树的区别在哪
有人会问了既然线段树的问题能够用树状数组解决而且线段树还比树状数组扩展性强,那为什么不直接用线段树呢?问的很好,树状数组的作用就是为了简化线段树,举个例子:一个问题可以用线段树解决写代码半个小时,但是用树状数组只需要10分钟,那么你会选择哪一个算法呢?没错,基于某些简单的问题,我们没必要用到功能性强但实现复杂的线段树(杀鸡焉用宰牛刀)。当并不是所有能用线段树解决的问题,用树状数组都可以解决。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










