激光多普勒测振系统将激光光束照射在粗糙目标表面,通过检测回波光束与 本振光束之间的相位差异来分析目标振动所产生的多普勒频率调制信息,从而获 得目标振动的位移、速度等物理量。
光
光的描述
为了更好地分析激光相干测振的原理,我们有必要对光的特性进行分析并推导出一定数学表达式对其运动状态进行描述。现代光学普遍认可光具有波粒二象性的观点。一方面,光的粒子性可以圆满地解释热辐射、光电效应、光压以及光的化学作用等光与物质相互作用的现象;另一方面,当面对干涉、衍射、偏振等光在空间中运动所产生的光学现象时,我们会考虑其波动的特性。由于本论文研究方向明显属于后者的范畴,所以在接下来的理论分析中将光束理解为特定频率范围的电磁波。
根据电磁理论,光在介质中的传播可用麦克斯韦方程来描述:
∇
×
E
=
−
∂
B
∂
t
,
∇
×
H
=
J
+
∂
D
∂
t
,
∇
⋅
D
=
ρ
,
∇
⋅
B
=
0.
\begin{aligned} \nabla \times \mathbf{E} &= - \frac{\partial \mathbf{B}}{\partial t}, \\ \nabla \times \mathbf{H} &= \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}, \\ \nabla \cdot \mathbf{D} &= \rho, \\ \nabla \cdot \mathbf{B} &= 0. \end{aligned}
∇×E∇×H∇⋅D∇⋅B=−∂t∂B,=J+∂t∂D,=ρ,=0.
式中, ∇ × \nabla \times ∇×代表旋度算子; ∇ \nabla ∇代表散度算符; H \mathbf{H} H代表磁场强度矢量; J \mathbf{J} J代表电流密度矢量; D \mathbf{D} D代表电位移矢量; E \mathbf{E} E代表电场强度矢量; B \mathbf{B} B代表磁感应强度矢量; ρ \rho ρ代表自由电荷密度。
光在无限大均匀绝缘介质中传播时,自由电荷密度 ρ = 0 \rho = 0 ρ=0,电导率 σ = 0 \sigma = 0 σ=0,且介电常数 ϵ \epsilon ϵ和磁导率 μ \mu μ为常量。由此可得光的波动方程:
∇ 2 E − 1 μ ϵ ∂ 2 E ∂ t 2 = 0 , ∇ 2 H − 1 μ ϵ ∂ 2 H ∂ t 2 = 0. \begin{aligned} \nabla^2 \mathbf{E} - \frac{1}{\mu \epsilon} \frac{\partial^2 \mathbf{E}}{\partial t^2} &= 0, \\ \nabla^2 \mathbf{H} - \frac{1}{\mu \epsilon} \frac{\partial^2 \mathbf{H}}{\partial t^2} &= 0. \end{aligned} ∇2E−μϵ1∂t2∂2E∇2H−μϵ1∂t2∂2H=0,=0.
这里, ∇ 2 \nabla^2 ∇2是拉普拉斯算子, ∂ 2 ∂ t 2 \frac{\partial^2}{\partial t^2} ∂t2∂2是对时间的二阶偏导数。
这里只需要考虑光束为平面波的情况。由于光束有唯一的传播方向,这个方向我们可以取为光以速度
v
v
v沿
x
x
x方向传播,其示意如图 2.1 所示。由此可得平面波的波动方程为:
∂
2
E
∂
x
2
−
1
μ
ϵ
∂
2
E
∂
t
2
=
0
,
\frac{\partial^2 \mathbf{E}}{\partial x^2} - \frac{1}{\mu \epsilon} \frac{\partial^2 \mathbf{E}}{\partial t^2} = 0,
∂x2∂2E−μϵ1∂t2∂2E=0,
∂
2
H
∂
x
2
−
1
μ
ϵ
∂
2
H
∂
t
2
=
0.
\frac{\partial^2 \mathbf{H}}{\partial x^2} - \frac{1}{\mu \epsilon} \frac{\partial^2 \mathbf{H}}{\partial t^2} = 0.
∂x2∂2H−μϵ1∂t2∂2H=0.
c
c
c是光在该介质中的速度,它等于
1
/
ϵ
μ
1/\sqrt{\epsilon \mu}
1/ϵμ

由于 H \mathbf{H} H和 E \mathbf{E} E满足关系 E = ϵ μ H \mathbf{E} = \sqrt{\epsilon \mu} \mathbf{H} E=ϵμH,在光学干涉测量的研究范围内,光振动矢量可直接用电场强度矢量来表示。由此可得沿 x x x轴正方向传播的平面余弦光波波动方程的解为:
E = E 0 cos ( 2 π ( f t − x λ ) + ϕ 0 ) E = E_0 \cos\left(2\pi (ft-\frac{x}{\lambda}) + \phi_0\right) E=E0cos(2π(ft−λx)+ϕ0)
式中, E 0 E_0 E0代表光波的振幅; f f f代表光波的频率; λ \lambda λ代表光波的波长; ϕ 0 \phi_0 ϕ0为光波的初相位。
则光波在任意坐标系中的复振幅描述为:
A = A 0 exp [ i ( K ⋅ r − 2 π f t ) ] A = A_0 \exp\left[i \left( \mathbf{K} \cdot \mathbf{r} - 2\pi ft \right)\right] A=A0exp[i(K⋅r−2πft)]
式中, A 0 A_0 A0代表光振动的振幅; K \mathbf{K} K代表激光的传播矢量, K = 2 π λ \mathbf{K} = \frac{2\pi}{\lambda} K=λ2π; r \mathbf{r} r代表在静止坐标系中光点的位置矢量。
光学混频概念
光学混频,就是当两束或两束以上不同频率的同伴光波一起致命到实体介质中时,在介质中发生电极化耦合,产生倍频、和频以及差频的现象。到非线性介质时,由幂级数分析法可以获得混频表达式为:
I
=
b
0
+
b
1
E
+
b
2
E
2
+
⋯
+
b
n
E
n
I=b_{0}+b_{1}E+b_{2}E^{2}+\cdots+b_{n}E^{n}
I=b0+b1E+b2E2+⋯+bnEn
式中, b0、 b1… bn 为常数,和非线性介质性质有关; E 为入射光合成光电场。 在实际操作时,如果接近线性,则一般取式子的前三项,即有:
I
≈
b
0
+
b
1
E
+
b
2
E
2
I\approx b_{0}+b_{1}E+b_{2}E^{2}
I≈b0+b1E+b2E2
当入射光为频率固定的单色光时,光电场强度为:
E
=
E
0
cos
w
E=E_{0}\cos w
E=E0cosw
式中, E0 为幅值; w 为角频率。则光混频后表达式为:
I
=
b
0
+
b
1
E
+
b
2
E
2
=
b
0
+
b
1
E
0
cos
w
t
+
b
2
E
0
2
cos
2
w
t
=
b
0
+
1
2
b
2
E
0
2
+
b
1
E
0
cos
w
t
+
1
2
b
2
E
0
2
cos
2
w
t
\begin{array}{l}{{I=b_{0}+b_{1}E+b_{2}E^{2}}}\\ {{=b_{0}+b_{1}E_{0}\cos{w t}+b_{2}E_{0}^{2}\cos^{2}{w t}}}\\ {=b_{0}+{\frac{1}{2}}b_{2}E_{0}^{~2}+b_{1}E_{0}\cos w t+{\frac{1}{2}}b_{2}E_{0}^{~2}\cos2wt}\end{array}
I=b0+b1E+b2E2=b0+b1E0coswt+b2E02cos2wt=b0+21b2E0 2+b1E0coswt+21b2E0 2cos2wt
式中的第三项为基频成分,第四项为倍频成分。当入射两种不同频率的光时,电场强度分别为:
E
1
=
E
01
cos
W
1
t
E_{1}=E_{\mathrm{01}}\cos_{W_{1}}t
E1=E01cosW1t
E
2
=
E
02
cos
W
2
t
E_{2}=E_{\mathrm{02}}\cos_{W_{2}}t
E2=E02cosW2t
式中,
E
01
E_{01}
E01、
E
02
E_{02}
E02分别为两光束电场强度的幅值;
w
1
w_1
w1、
w
2
w_2
w2分别为两束光的角频率。 两束光的合成电场强度为:
E
=
E
1
+
E
2
=
E
01
cos
w
1
t
+
E
02
cos
w
2
t
E=E_{1}+E_{2}=E_{01}\cos{w_{1}}t+E_{02}\cos{w_{2}t}
E=E1+E2=E01cosw1t+E02cosw2t
则混频后光强为:
E
=
b
0
+
b
1
(
E
o
l
cos
w
i
t
+
E
o
2
cos
w
2
t
)
+
E=b_{0}+b_{1}\left(E_{\mathrm{ol}}\cos{w_{\mathrm{i}}t}+E_{\mathrm{o2}}\cos{w_{2}t}\right)+
E=b0+b1(Eolcoswit+Eo2cosw2t)+
1 2 b 2 ( E 01 2 + E 02 2 + E 01 2 cos 2 w 1 t + E 02 2 cos 2 w 2 t ) + \frac{1}{2}b_{2}\left(E_{01}^{2}+E_{02}^{2}+E_{01}^{~2}\cos^{2}w_{1}t+E_{02}^{2}\cos^{2}w_{2}t\right)+ 21b2(E012+E022+E01 2cos2w1t+E022cos2w2t)+
b
2
E
01
E
02
cos
(
w
1
+
w
2
)
t
+
b
2
E
01
E
02
cos
(
w
1
−
w
2
)
t
b_{2}E_{01}E_{02}\cos(w_{1}+w_{2})t+b_{2}E_{01}E_{02}\cos\bigl(w_{1}-w_{2}\bigr)t
b2E01E02cos(w1+w2)t+b2E01E02cos(w1−w2)t
从式中可以看出最后两项为和频成分与差频成分。通过选频网络就可以将需要的差 频成分选择出来,这就是光学混频技术的原理。
光学拍频概念
当两个幅值和频率相近的简谐波进行叠加时,会出现幅值忽高忽低的现象,也就是所谓的“拍”现象,但它又不同于幅值调制,虽然在时域上表现相同:都是幅值忽高忽低,但二者有着本质的区别。当两个频率相近的声波叠加时,由于人耳听到的声音取决于声波的幅值,因此,当出现拍现象时,人耳听到的声音在幅值上会出现周期性的强弱变化,一强一弱变化就是一次拍。

当同方向的两个频率相差不大的简谐波叠加时,叠加后的波形的幅值将随时间作强弱的周期性度化,这种现象称之为“拍”,如图所示,图中有三个拍,幅值出现忽强忽弱的变化,单位时间内出现的拍数称为拍频(拍的频率),也是叠加后波形的幅值变化频率。
两个振幅相同 、振动方向相同、同方向传播,但频率接近的单色光波的叠加,将产生光学拍。
通常,原始的两个简谐波的振动频率较高,与叠加后的波形的频率接近,但拍的频率很低,远小于原始简谐波的振动频率,因而,当出现拍现象时,它把高频信号中的频率信息和相位信息转移到低频信号(拍)之中,使它们由难以测量变得容易测量。

里面的高频探测器响应不到,但探测器可以响应到轮廓线的频率。
原理公式:

混频和拍频
光学拍频(Optical Beat Frequency)和光学混频(Optical Mixing or Frequency Mixing)都是光学干涉和非线性光学的现象,但它们有一些基本的不同。
光学拍频:
- 机制:发生在两个或更多的接近频率的光波相互干涉时。
- 输出:生成一个新的光波模式,其强度随时间周期性变化。这个变化的频率是原始光波频率之间的差值。
- 线性现象:这是一个线性光学现象,不需要非线性介质。
- 应用:常用于光谱分析、高分辨率距离测量、光学通信等。
光学混频:
- 机制:当两个不同频率的光波进入一个非线性光学材料时,它们会相互作用并产生新的频率。
上述的相互作用的具体情况主要看非线性光学材料的性质,可能是两者相乘也可能是其他情况。
但混频器原理好像就是两个信号相乘,不知道有没有其他情况。
- 输出:生成的新频率通常是原始频率的和或差 ( ω 3 = ω 1 ± ω 2 (\omega_3 = \omega_1 \pm \omega_2 (ω3=ω1±ω2),还可能包括更复杂的频率组合。
- 非线性现象:这是一个非线性光学现象,需要非线性介质。
- 应用:常用于频率转换、参数振荡、二次谐波生成(SHG)和其他非线性光学应用。
简言之,光学拍频是一种线性现象,通常涉及相近的频率,而光学混频是一种非线性现象,涉及的频率可以相差很大,并且需要非线性介质来产生新的频率。
非线性光学材料的原理待补充
混频
“混频”(Mixing)是一个广泛的概念,可以用于描述多种物理现象,其中包括电子和光学系统。基本上,它涉及两个或更多不同频率的信号相互作用,生成新的信号,这些新信号的频率通常是原始频率的和或差。“光学混频”(Optical
Mixing)则是混频的一个特定子集,专门用于描述在光学系统中出现的混频现象。在光学混频中,两个或多个不同频率的光波通过非线性光学介质相互作用,生成新的光波,其频率为输入光频率的和或差。主要区别:
物理域: 混频可以在多个物理领域出现(例如电子、声学、光学等),而光学混频特指光学领域内的混频现象。
工作介质: 在普通的混频中,介质可以是电子电路(例如混频器或者调制解调器)或其他物理系统。而在光学混频中,介质通常是某种非线性光学材料。
应用领域: 混频广泛应用于通信、无线电、音频处理等,而光学混频通常应用于光学通信、激光频率转换、光谱学等。
非线性系数: 在光学混频中,通常需要使用具有高非线性系数的介质,以便在低功率下也能实现有效的混频。
效率: 由于光学系统中可以使用高质量、高非线性的光学材料,因此光学混频通常具有较高的转换效率。
生成频率: 在电子混频中,通常生成的是低频信号(例如音频频率)。而在光学混频中,生成的是光频信号,频率范围相对更广。
这些区别使得光学混频和一般的混频虽然在基本原理上相似,但在应用和实现上有明显不同。
激光多普勒效应理论
多普勒效应基本概念
任意物质或者波源相对于观察参考系发生任意方向的相对运动时,观察位置 所接收到的表观观测频率与波源的真实频率不同,这种因运动所产生的频率变化 现象被叫做多普勒效应。多普勒效应于 1842 年由 Austria 天文学家 Christian Doppler 首次提出用于对恒星彩色光效应现象的理论解释,这种现象表明观察 参考系所接收的实际频率值与信号源相对于观察者的速度大小和方向相关。当信 号源靠近观察者时,观察者的收到表观频率值将大于信号源的实际频率,而当信 号源远离观察者时,观测得到的频率值将小于信号源的实际频率。

多普勒效应是物质具有波动性的重要表现形式,如上图所示,假设信号源S 在给定可传播介质的实际波速为 V,频率为 f。若信号源以速度为 vs,沿着与观测点 P 视线方向的夹角角度为θ的方向运动,则在观测点 P 处所感知的表观观测频率为:
f
′
=
V
V
−
ν
s
cos
θ
s
f
=
1
1
−
ν
s
cos
θ
s
/
V
f
f^{\prime}={\frac{V}{V-{\nu}_{s}\cos{\theta_{s}}}}f={\frac{1}{1-{\nu}_{s}\cos{\theta_{s}}/{V}}}{\mathcal{f}}
f′=V−νscosθsVf=1−νscosθs/V1f
若当 v s V < < 1 \frac{v_s}{V} << 1 Vvs<<1,使用麦克劳林展开进行近似(仅取一次项):
f ′ ≈ f ( 1 + v s cos θ s V ) f' \approx f \left( 1 + \frac{v_s \cos \theta_s}{V} \right) f′≈f(1+Vvscosθs)
若当信号源静止,而观测点 P 以速度为 vp,夹角方向为 θp运动时, 观测点 P 测得的表观观测频率为
f ′ = f ( 1 + v p cos θ p V ) f' = f \left( 1 + \frac{v_p \cos \theta_p}{V} \right) f′=f(1+Vvpcosθp)
当信号源和观测者都在运动
f ′ = f ( ( 1 + v p cos θ p V ) 1 + v s cos θ s V ) f' = f \left( \frac{( 1 + \frac{v_p \cos \theta_p}{V})}{1 + \frac{v_s \cos \theta_s}{V}} \right) f′=f(1+Vvscosθs(1+Vvpcosθp))
激光多普勒效应

如上图所示的收发分离的激光多普勒探测系统,激光多普勒探测系统的发 射机与其相对应的接收机分别位于 O 与 Q 两点,二者之间的距离为 L。探测系 统的发射机发射的特定波长的激光信号照射在粗糙目标 P 的表面时,将会与目 标表面信息相互作用并发生散射,其中部分散射光将会返回探测系统的接收模块, 接收模块能收到经过目标表面信息调制的散射回波信号。当目标相对于探测系统 保持静止时,接收机接收到的回波散射信号与发射端的发射信号只存在固定常数 的相位偏移。而目标 P 相对于探测系统存在任意方向的相对运动时,探测系统的 接收端收到的回波信号将会在固定相移的基础上发生额外随时间变化的相位偏 移。这种额外的相移是由目标运动所引起的多普勒频移所造成的,这额外的多普勒频移就是激光多普勒效应。
对于电磁波或光波来说,波源的传播速度 c 是常数。但光多普勒效应与经典 多普勒效应有区别的地方在于,光多普勒效应在计算目标与探测系统之间相对运 动所产生的多普勒频移需要考虑相对论中的时间膨胀效应。假设发射机所发 出的光频率记为 f p o f_{po} fpo。当目标 P 以速度为 v,沿着与发射机夹角为 θ T θ_T θT,与接收机 夹角为 θ R θ_R θR的方位运动时,以目标 P 所在位置建立参考系,则在目标 P 处所观测 到的发射信号光表观频率 f p o f_{po} fpo为:
对于电磁波或光波,波源的传播速度 c c c确实是常数,通常是 3 × 1 0 8 m/s 3 \times 10^8 \, \text{m/s} 3×108m/s。相对论多普勒效应确实需要考虑时间膨胀和长度收缩效应,尤其当相对速度 v v v接近光速 c c c时。
设发射机发出的频率为 f PO f_{\text{PO}} fPO,目标 P P P以速度 v v v运动,相对于发射机的夹角为 θ T \theta_T θT,相对于接收机的夹角为 θ R \theta_R θR。
在目标 P P P的参考系下,观测到的发射信号光的表观频率 f P O f_{PO} fPO可以使用以下相对论多普勒效应公式来描述:
f PO = f ( 1 − v c cos θ T 1 − v 2 c 2 ) = f ( 1 − v c cos θ T ) ∗ γ f_{\text{PO}} = f \left( \frac{1 - \frac{v}{c} \cos \theta_T}{\sqrt{1 - \frac{v^2}{c^2}}} \right) = f \left( {1 - \frac{v}{c} \cos \theta_T} \right) *γ fPO=f 1−c2v21−cvcosθT =f(1−cvcosθT)∗γ
而接收机所探测得到的目标 P 所散射的回波表观观测频率 f Q P f_{QP} fQP为:
f QP = f P O ( 1 ( 1 − v c cos θ T ) ∗ γ ) = f ( 1 + v c cos θ T 1 − v c cos θ R ) f_{\text{QP}} = f_{PO} \left( \frac{1}{(1 - \frac{v}{c} \cos \theta_T)*γ} \right) = f \left (\frac{1 + \frac{v}{c} \cos \theta_T} {1 - \frac{v}{c} \cos \theta_R}\right) fQP=fPO((1−cvcosθT)∗γ1)=f(1−cvcosθR1+cvcosθT)
其中 c 为光在真空中传播的速度, γ γ γ为相对论时间膨胀因子
在特殊相对论中,Lorentz因子(也称为时间膨胀因子或γ因子)通常定义为:
γ = 1 1 − v 2 c 2 \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} γ=1−c2v21
此因子用于调整在相对速度下观察到的时间和长度。在时间膨胀的情境下,相对于静止观察者,运动物体的内部时间流逝得更慢,这种减缓的程度由$
\gamma$控制。如果使用 γ = 1 − v 2 c 2 \gamma = \sqrt{1 - \frac{v^2}{c^2} } γ=1−c2v2,那么在 v v v接近 c c c
时,因子会接近零,这与实际观察不符。实际上,当一个物体接近光速时,其内部时间流逝会显著减缓(相对于在静止或低速下观察),因此$
\gamma$应该是一个大于 1 的数。所以,正确的 Lorentz 因子或 γ \gamma γ因子是 1 1 − v 2 c 2 \frac{1}{\sqrt{1 -\frac{v^2}{c^2}}} 1−c2v21,而不是 1 − v 2 c 2 \sqrt{1 - \frac{v^2}{c^2} } 1−c2v2。这样的设置是为了确保当物体接近光速运动时,相关的物理量(如时间、能量等)会以正确的方式发生变化。
θT 是发射机与目标运动方向的夹角, θR 是接收机与目标运动方向的夹角。通常,目标 P 的振动的速度远小于光速,即
v
<
<
c
v<<c
v<<c,因此将式(2-6)利用 Maclaurin 展开:
f
Q
P
=
(
1
+
ν
c
cos
θ
T
+
ν
c
cos
θ
R
)
f
f_{Q P}=\left(1+{\frac{\nu}{c}}\cos\theta_{T}+{\frac{\nu}{c}}\cos\theta_{R}\right)f
fQP=(1+cνcosθT+cνcosθR)f
激光多普勒探测系统所探测到的多普勒频移可以表示为探测系统接收机的 观察频率与发射信号实际频率之差:
Δ
f
=
f
Q
P
−
f
=
v
c
(
cos
θ
T
+
cos
θ
R
)
f
\Delta\!f=f_{Q P}-f={\frac{v}{c}}\!\left(\cos\theta_{T}+\cos\theta_{R}\right)\!f_{}
Δf=fQP−f=cv(cosθT+cosθR)f
进而采用三角和差化积公式,
Δ
f
=
2
f
ν
c
cos
θ
R
+
θ
T
2
cos
θ
R
−
θ
T
2
\Delta\!f=\frac{2f\nu}{c}\cos\frac{\theta_{R}+\theta_{T}}{2}\cos\frac{\theta_{R}-\theta_{T}}{2}
Δf=c2fνcos2θR+θTcos2θR−θT
从图 2.2 的几何关系不难得出:
θ
R
−
θ
T
=
φ
,
θ
R
+
θ
T
=
2
δ
\theta_{R}-\theta_{_T}=\varphi\;,\;\;\;\theta_{R}+\theta_{_T}=2δ
θR−θT=φ,θR+θT=2δ
其中φ是激光多普勒探测系统发射端与接收端之间的夹角,δ称为探测系统双基角,是双基角角 平分线与目标运动方向之间的夹角,称为目标方位角。因此,收发分离激光多普 勒探测系统所探测到的目标多普勒频移可表示为:
Δ
f
=
2
f
ν
c
cos
δ
G
O
S
(
φ
2
)
\Delta f={\frac{2f\nu}{c}}\cos\delta\,\mathrm{GOS}\left(\frac{\varphi}{2}\right)
Δf=c2fνcosδGOS(2φ)
在收发一体的激光多普勒探测系统中,满足发送端与接收端之间的距离 L= 0,从而有探测系统双基角 φ=0 。当目标沿着激光多普勒探测系统的视线方向运动时,定义目标沿着远离系统方向的运动速度为正,此时目标运动的方位角
δ
=
Π
δ=Π
δ=Π,则收发一体的激光多普勒探测系统所探测到的目标多普勒平移量可以表示为:
Δ
f
=
−
2
f
ν
c
=
−
2
ν
λ
\Delta\!f=-\frac{2f\nu}{c}=-\frac{2\nu}{\lambda}
Δf=−c2fν=−λ2ν
式中,
Δ
f
Δf
Δf为多普勒频率,为非负值。由上式可知物体振动的瞬时速度和多普勒频移成正比,在速度方向、光源位置和光电探测器位置已知时,只要测出
Δ
f
Δf
Δf就可计算出物体 速度的大小
V
V
V,进而得到振动的位移和加速度。
激光多普勒测振原理
激光雷达技术分类

相干测量
- 零差探测(Homodyne Detection):在这种方式下,参考光与信号光具有相同的频率。这种方法通常更简单但可能对噪音更敏感。
简单性:零差技术相对更简单,因为它只涉及单一频率的信号。
解调容易:由于没有频率转换,解调过程相对简单。
成本:通常成本更低,因为不需要高精度的频率或时间参考。
信噪比限制:在高噪声环境下,信噪比可能不如外差技术。
灵敏度限制:对于微弱信号的检测,零差方式可能不如外差方式灵敏。
- 外差探测(Heterodyne Detection):在这里,参考光的频率与信号光稍有不同,从而生成一个外差信号(两者的频率差)。这种方法可以提供更高的灵敏度,并允许更复杂的信号处理。
频率灵活性: 外差技术通过混频来检测两个不同频率的信号,因此更加灵活。
灵敏度: 通常情况下,外差技术具有更高的灵敏度。
解调难度: 由于信号需要和一个参考信号(通常具有不同的频率)混合,因此解调相对复杂。
信噪比: 在高噪声环境下,外差技术可能提供更好的信噪比。
多信号处理: 适用于多信号的复杂情境,因为可以通过混频将不同频率的信号分开。
成本: 通常需要更高精度的时间或频率参考,成本相对较高。
直接测量
-
模拟探测(Analog Detection):这种方法通常使用连续波激光和光电探测器直接测量返回信号的强度。它是最简单的方法,但可能不适用于复杂或多目标的场景。
-
单光子探测(Single-Photon Detection):这是一种非常灵敏的探测方式,它能够在极低光级别下工作。这种方法通常用于长距离或非常暗的环境。
激光相干探测原理
激光多普勒测振系统是基于激光多普勒效应理论以及激光相干探测理论的 高精度测量设备。由于被检测目标的运动,通过探测器接收到的携带有多普勒频 移物体的回波散射光,就可以获取物体运动速度和位移。由于常见的激光的频率远远高于微波雷达,如基于可见光结构的激光多普勒测振仪所采用的 632nm 波 长的激光,而现有的光学探测器无法直接响应如此高的频率,因此通常采用相干测量的手段来间接获取回波散射光中的多普勒频移。

零差探测(直流干涉
在零差检测中,待测电磁波和一个已知的参考信号(经常被称作本地振荡器)进行混波,而待测信号和参考信号的载频是相同的,这样得到的干涉光场可以消除电磁波本身频率噪声所带来的影响。经典的光学零差检波装置如马赫-曾德尔干涉仪与迈克尔逊干涉仪,其待测信号和参考信号来自同一波源。

零差探测激光干涉仪大多采用迈克尔逊干涉仪的光路,白光会改成单色激光,增强光路的单色性。

频率为
f
0
f_0
f0的激光通过分光镜后分为两束,其中一束作为测量光照射到运动的物体上, 被振动物体反射后产生多普勒频移,其频率为
f
0
±
f
D
f_0±f_D
f0±fD,携带振动信息的测量光与另一束 参考光相遇并一同照射到光电探测器上进行光混频,经选频网络后输出频率为
f
D
f_D
fD的光电信号。可得其速度公式为:
V
=
∣
λ
2
cos
θ
f
D
∣
\mathrm{{V=\left|{\frac{\lambda}{2\cos\theta}}f_{D}\right|}}
V=
2cosθλfD
不难看出这种零差干涉只能测出振动速度的大小,并不能对速度方向进行判断, 而且所得频移信号为低频微弱信号,特别容易受噪声干扰,发生直流漂移,影响测量精 度。
为什么零差信号会丧失速度方向?
在多普勒效应的基础上,假设原激光频率为 f 0 f_0 f0,多普勒频移为 f D f_D fD。物体运动时反射的光的频率可以为 f 0 + f D f_0+f_D f0+fD(远离观察者)或 f 0 − f D f_0-f_D f0−fD(靠近观察者)。在零差多普勒系统中,这个反射的光会与原激光(参考光,频率为
f 0 f_0 f0)进行混合。混频后的信号包含两个主要成分,其频率为两光源频率之差或之和。因此,对于远离和靠近观察者两种情况,混频后的光电信号可以表示为:
- 远离观察者: f 0 + f D − f 0 = f D f_0 + f_D - f_0 = f_D f0+fD−f0=fD
- 靠近观察者: f 0 − f D − f 0 = − f D f_0 - f_D - f_0 = -f_D f0−fD−f0=−fD
然而,在接下来的信号处理步骤中,一般会提取这两种情况的绝对值,即 ∣ f D ∣ |f_D| ∣fD∣??????。因此,无论物体是远离还是靠近观察者,输出的
∣ f D ∣ |f_D| ∣fD∣ 都是一样的,从而丧失了方向信息。简言之,由于混频后信号处理通常只考虑 f D f_D fD
的绝对值,所以方向信息会丢失。这也是为什么在零差多普勒测速系统中,速度的方向信息通常是不可得的。
难道是因为cos时是偶函数?????
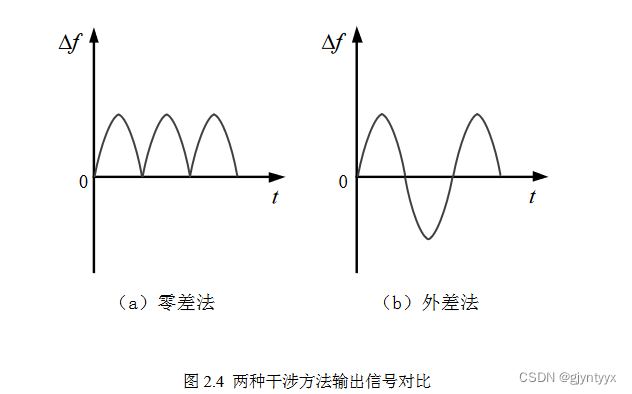
外差探测
如果参考光束和测量光束之间有一定的频差,当输出光电信号时,就相当于把多普勒频移信号载在一个固定的频率上,干涉后被测信号是通过该频率的载波信号传递,这就是外差测量。与零差法相比,外差测量不仅可 以判断物体运动方向,而且增强了抑制噪声的能力,提高了测量精度。
获取载波途径:
既然选择了外差干涉的光学结构,那么需要慎重考虑的问题就是如何获得稳定的频 差。目前来说,激光调频主要分为内调制和外调制两类,内调制是指调制在激光振荡的过程中进行,通过改变振荡参数的方法达到改变激光输出特性的目的,主要包括双频激光器等,使用这类调制方 法可以简化测量光路,但调制技术不够成熟,调制的激光不够稳定,而且如何形成同步 的外差结构也是一个比较难解决的问题,所以目前应用较少。外调制不会改变激光器的参数,而是通过改变已经输出激光的参数来达到调制的目的,主要包括电光调制、声光 调制和磁光调制三种,应用比较广泛。其中电光调制技术的调制频率和其半波电压有关, 当需要产生比较大的频差时其使用受到一定限制,而磁光调制技术最大只能产生 3MHz 的频差,也不太符合本测量系统的使用要求,所以相对来说声光调制技术比较合适,调制频率很高且频差稳定,是当前应用最普遍的一种频率调制技术
声光调制(记录一下还没看懂
当频率固定的超声波在声光晶体介质中传播时,由于超声波为纵波,其传播特点为 质点的振动方向和波的传播方向平行,因此会使得声光晶体内部各质点沿着波传播方向 发生振动,相当于产生周期性变化挤压力和拉伸力,使晶体介质内部产生疏密程度的变 化,从而晶体折射率也发生周期性的变化,当光波通过时,由于折射率的不同,产生衍 射现象,相当于对光波的频率和相位进行了调制,这就是声光效应的产生原理。由于声 光效应可以达到控制激光频率和相位的目的,因而应用这种原理制作的声光器件,在光 通信和光干涉测量领域应用非常广泛。
声光效应主要有两种典型的衍射类型,分别为拉曼-纳斯衍射和布拉格衍射。区分的依据为:
Q = 2 π L ( λ λ S ) (2.27) Q = {2\pi L} \left( \frac{\lambda}{\lambda_S} \right) \quad \text{(2.27)} Q=2πL(λSλ)(2.27)
式中, L L L为声光互相作用长度; λ \lambda λ为入射光波长; λ S \lambda_S λS为超声波波长。一般来说,当 Q ≤ 0.3 Q \leq 0.3 Q≤0.3时发生拉曼-纳斯衍射,当 Q ≥ 4 π Q \geq 4\pi Q≥4π时发生布拉格衍射,在 0.3 ≤ Q ≤ 4 π 0.3 \leq Q \leq 4\pi 0.3≤Q≤4π 的条件下,衍射情况比较复杂。
n 表示声光晶体的折射率,这个又如何推导?
当超声波的频率较低,声光互作用的长度比较短时,发生拉曼-纳斯衍射,此时所产生的衍射光对称分布在零级条纹两侧,和常见的光学光栅所产生的衍射光分布规律基本相同。由于拉曼-纳斯衍射的衍射光束是多级的对称分布的,从中选择某一级衍射光的难度较大,且由于声光互相作用长度 L L L 必须很短,会导致衍射效率不高,所以在频率调制方面应用受限。
相比较而言,布拉格衍射可以只留下 0 级和+1 级(或-1 级)衍射光,衍射效率较高,更适合进行激光频率的外调制。布拉格衍射如图 2.5 所示,下面我们就对其原理进行具体分析。
由于光速比声波的传播速度快很多,正常情况下可以近似将在光波通过这段时间内声光介质在空间上的周期变化看作是固定不变的。当超声波在声光晶体中传播时,介质折射率的变化为:
Δ
(
1
/
n
2
)
=
p
S
(2.28)
\Delta(1/ n^2) = pS \text{(2.28)}
Δ(1/n2)=pS(2.28)
式中,
n
n
n 为声光介质的折射率;
p
p
p 为光弹系数;
S
S
S 为超声波作用下的应变。
假设超声波沿
y
y
y 方向传播,则其对介质的应变可以写成:
S
=
S
0
sin
(
ω
S
t
−
k
S
y
)
(2.29)
S = S_0 \sin(\omega_S t - k_S y) \quad \text{(2.29)}
S=S0sin(ωSt−kSy)(2.29)
式中,
S
0
S_0
S0 为应变幅值;
ω
S
\omega_S
ωS 为超声波传播角频率;
k
S
k_S
kS 为角波数;
y
y
y 为位置。当应变较小时,折射率的变化方程位:
n
(
y
,
t
)
=
n
0
+
Δ
n
sin
(
ω
S
t
−
k
S
y
)
n(y,t) = n_0+ \Delta n \sin(\omega_S t - k_S y)
n(y,t)=n0+Δnsin(ωSt−kSy)
式中, n 0 n_0 n0为无超声波时声光介质的折射率; Δ n \Delta n Δn为声光介质折射率变化的幅值,可由式(2.28)求得,由此可得衍射情况。当超声波的频率很高,声光互作用长度 L L L较长,即 Q ≥ 4 π Q \geq 4\pi Q≥4π,满足布拉格衍射条件时,激光以一定角度入射到声光晶体中,整个声光晶体相当于体光栅,各高次衍射光抵消,只有 0 级和+1 级(或-1 级)衍射光存在。
此时光束的入射角
θ
B
\theta_B
θB称为布拉格角,其大小满足:
sin
θ
B
=
λ
2
λ
s
(2.31)
\sin \theta_B = \frac{\lambda}{2\lambda_s} \quad \text{(2.31)}
sinθB=2λsλ(2.31)
式中,
λ
S
\lambda_S
λS为超声波的波长;
λ
\lambda
λ为入射光波的波长。此公式为布拉格条件。
由于布拉格角非常小,所以
±
1
\pm 1
±1级衍射光对入射光的偏转角为:
ϕ
≈
2
θ
B
=
λ
λ
s
=
λ
f
s
V
s
(2.32)
\phi \approx 2\theta_B = \frac{λ}{λ_s}=\frac{\lambda f_s}{V_s} \quad \text{(2.32)}
ϕ≈2θB=λsλ=Vsλfs(2.32)
式中,
V
S
V_S
VS为超声波传播速度;
f
S
f_S
fS为超声波频率。
m
m
m级衍射光的频率为:
ω
m
=
ω
0
±
m
ω
s
(
m
=
0
或
±
1
)
(2.33)
\omega_m = \omega_0 \pm m \omega_s (m= 0 或 ±1) \quad \text{(2.33)}
ωm=ω0±mωs(m=0或±1)(2.33)
式中,
ω
\omega
ω为入射光的频率。
±
1
\pm 1
±1级衍射光的衍射效率为:
η
=
[
sin
2
(
π
λ
M
2
L
P
s
2
H
)
]
(2.34)
\eta = \left[ \sin^2 \left( \frac{\pi}{\lambda} \sqrt\frac{M_2LP_s}{2H} \right) \right]\quad \text{(2.34)}
η=[sin2(λπ2HM2LPs)](2.34)

式中, M 2 M_2 M2为常数,与声光晶体本身属性有关;L 和 H 分别为超声换能器的长和宽; P s P_s Ps为超声功率。可以通过控制超声波功率来达到控制衍射效率的作用,而且理论上只要 超声功率足够大,就能够使衍射效率达到100% 。
通过对声光调制的理论研究可以得出,我们可以通过改变加载在电声换能器上的驱 动电信号来控制超声波的频率和功率,进而达到对光束频率和衍射效率的控制,为外差 干涉结构提供稳定的频差。传统的激光多普勒测振系统典型外差为 40MHz,综合考虑 光学干涉测量条件和声光调制效率,发现在 80~120MHz 的频差范围内可以有效提高系 统测量分辨率。
基于声光调制的外差干涉仪1
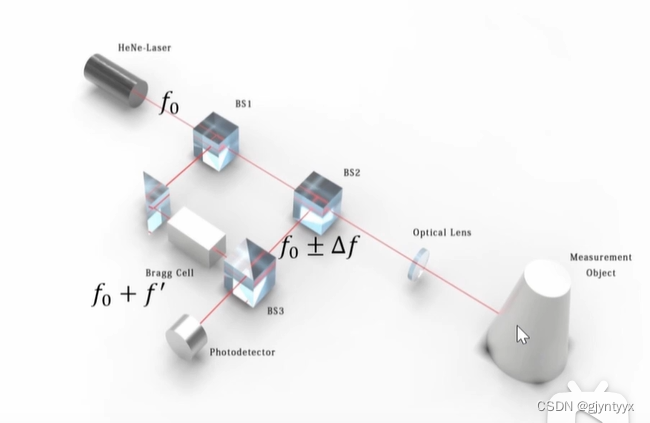

如图所示的可见光结构的激光相干多普勒探测系统,由激光光源发出的 相干激光光束经过偏振分光棱镜 PBS1 分为本振光和信号光,在本振光路上放置 声光调制器对本振光进行调制。声光调制器作用是让本振参考光额外附加一个固 定的频移
f
A
O
M
f_{AOM}
fAOM,产生的固定声光频移的值通常被称为中频频率,这种配置被称 为外差相干探测,采用外差配置可分辨物体振动的方向。信号光经过 PBS2 后, 经聚焦光学系统会聚在运动目标的粗糙表面上。由于目标的运动,使得照射在目 标表面上的这一部分信号光受到多普勒调制,并产生额外的多普勒频移。当聚焦 光学系统获得到带有目标运动信息的回波散射光信号后,与经过声光调制器调制 的本振光经过合束棱镜 BS 后在探测器的光敏面上叠加混频。假设本振光的起始位相为 0,则混频后的光波函数可以表示为:
E
⃗
(
x
,
y
,
t
)
=
E
⃗
L
O
(
x
,
y
)
exp
[
j
2
π
(
f
o
+
f
A
O
M
)
t
]
+
E
⃗
S
R
(
x
,
y
)
exp
[
j
2
π
(
f
o
+
f
d
)
t
+
ϕ
(
t
)
]
\begin{array}{c}{{\vec{E}\left(x,y,t\right)=\vec{E}_{LO}\left(x,y\right)\exp\left[j2\pi\left(f_{o}+f_{AOM}\right)t\right]+}}\\ {{\vec{E}_{SR}\left(x,y\right)\exp\left[j2\pi\left(f_{o}+f_{d}\right)t+\phi\left(t\right)\right]}}\end{array}
E(x,y,t)=ELO(x,y)exp[j2π(fo+fAOM)t]+ESR(x,y)exp[j2π(fo+fd)t+ϕ(t)]
搞不清楚用的是混频还是拍频,在查阅资料的时候发现在说明外差干涉仪原理时,两种说法都有提到。
这部分就用混频来了
在描述激光多普勒测速或激光相干测振的背景下,本振(Local Oscillator, LO)和信号(Signal, SR)通常用复振幅 E L O ( x , y ) E_{LO}(x, y) ELO(x,y)和 E S R ( x , y ) E_{SR}(x, y) ESR(x,y)表示。其中, f o f_o fo是激光器发出的光频率, f d f_d fd是由于目标运动导致的多普勒频移。 ϕ ( t ) \phi(t) ϕ(t)是由系统和环境噪声引起的随机相位干扰和探测器接收到的本振光与回波信号光之间的相位差的总和。
在这样的情境下,光电探测器上采集到的总输出光强
I
(
t
)
I(t)
I(t)可以表示为:
I
t
o
t
a
l
(
t
)
=
I
L
O
+
I
S
R
+
I
H
I_{t o t a l}\left(t\right)=I_{L O}+I_{S R}+I_{H}
Itotal(t)=ILO+ISR+IH
=
∬
β
(
x
,
y
)
[
E
⃗
L
O
(
x
,
y
)
]
2
d
x
d
y
+
∬
β
(
x
,
y
)
[
E
⃗
s
R
(
x
,
y
)
]
2
d
x
d
y
+
=\textstyle\iint\beta(x,y)\ \!\left[{\vec{E}}_{L O}\left(x,y\right)\right]^{2}d x d y+\textstyle\iint\beta(x,y)\ \!\left[{\vec{E}}_{s R}\left(x,y\right)\right]^{2}d x d y+
=∬β(x,y) [ELO(x,y)]2dxdy+∬β(x,y) [EsR(x,y)]2dxdy+
2
R
e
(
∫
∫
β
(
x
,
y
)
E
⃗
L
o
(
x
,
y
)
E
⃗
S
R
∗
(
x
,
y
)
e
x
p
[
j
2
π
(
f
A
O
M
+
f
d
)
t
+
ϕ
(
t
)
]
d
x
d
y
)
2\,\mathrm{Re}\Big(\int\int\beta(x,y)\vec{E}_{L o}\,(x,y)\,\vec{E}_{SR }^{\ast}(x,y)\,\mathrm{exp}\Big[j2\pi\big(f_{AOM}+f_{d}\big)t+\phi(t)\Big]d x d y\Big)
2Re(∫∫β(x,y)ELo(x,y)ESR∗(x,y)exp[j2π(fAOM+fd)t+ϕ(t)]dxdy)
这里, ∣ ⋅ ∣ 2 | \cdot |^2 ∣⋅∣2表示取复数的模的平方。这个公式考虑了多普勒效应(通过 f d f_d fd)和随机相位干扰 ϕ ( t ) \phi(t) ϕ(t)。
注意:这里的公式是一个简化的版本,实际应用可能需要更复杂的模型来考虑各种因素,如介质的非均匀性、光束的不完美性等。
考虑到探测器的响应强度 β ( x , y ) = η ( x , y ) ⋅ e / h ν \beta(x,y) =\eta(x,y) \cdot e/ h \nu β(x,y)=η(x,y)⋅e/hν,其中 η ( x , y ) \eta(x, y) η(x,y)是单位量子效率, e e e是电子的电荷量, h h h是普朗克常数, ν \nu ν是光量子的频率。
设光电探测器的量子效率是均匀的。这样,总输出光强 I ( t ) I(t) I(t)的三个组成部分可以分别用以下三个公式表示:、
光电探测器(Photo-detector 或 Photodetector) 是一种能够将光信号转换为电信号的设备。这些探测器有多种类型,包括光电二极管、光电倍增管、PIN二极管、雪崩光电二极管(Avalanche Photodiodes, APDs)等。每一种光电探测器都有其特定的应用、灵敏度、响应时间和其他性能指标。
主要工作原理:
光吸收:当光子撞击到探测器表面的半导体材料时,它们会将能量传递给半导体中的电子。
激发与复合:这些电子会获得足够的能量跃迁到导带,从而生成电子-空穴对。
电荷收集:然后,通过外部电路或者内部电场,这些电子和空穴会被分开并流向电极,从而产生一个可测量的电流或电压。
需要进一步了解
I
L
O
=
∫
∫
β
(
x
,
y
)
[
E
⃗
L
O
(
x
,
y
)
]
2
d
x
d
y
I_{LO}=\int\int\beta\Big(x,y\Big)\Big[\vec{E}_{L O}\Big(x,y\Big)\Big]^{2}\,d x d y
ILO=∫∫β(x,y)[ELO(x,y)]2dxdy
I
S
R
=
∫
∫
β
(
x
,
y
)
[
E
⃗
S
R
(
x
,
y
)
]
2
d
x
d
y
I_{_{S R}}=\int\!\!\!\int\beta\Big(x,y)\bigg[\vec{{{E}}}_{S R}\left(x,y\right)\bigg]^{2}\,d x d y
ISR=∫∫β(x,y)[ESR(x,y)]2dxdy
I
H
(
t
)
=
2
R
e
(
∫
∫
β
(
x
,
y
)
E
ˉ
L
O
(
x
,
y
)
E
ˉ
S
R
(
x
,
y
)
e
x
p
[
j
2
π
(
f
A
O
M
+
f
d
)
t
+
ϕ
(
t
)
]
d
x
d
y
]
=
2
β
I
L
O
I
S
R
c
o
s
[
2
π
(
f
A
O
M
+
f
d
)
t
+
ϕ
(
t
)
]
I_{H}\left(t\right)=2\,\mathrm{Re}\Bigl(\int\int\beta\left(x,y\right)\bar{E}_{LO}\left(x,y\right)\bar{E}_{SR}\left(x,y\right)\mathrm{exp}\Bigl[\,j2\pi\left(f_{AOM}+f_{d}\right)t+\phi\Bigl(t\Bigr)\Bigr]d x d y\Bigr] =2\beta\sqrt{I_{L O}I_{SR }}\;\mathrm{cos}\Big[2\pi\Big(\cal f_{AOM}+\cal f_{d}\Big)t+\phi\Big(t\Big)\Big]
IH(t)=2Re(∫∫β(x,y)EˉLO(x,y)EˉSR(x,y)exp[j2π(fAOM+fd)t+ϕ(t)]dxdy]=2βILOISRcos[2π(fAOM+fd)t+ϕ(t)]
其中 I L O I_{LO} ILO和 I S R I_{SR} ISR是本振(Local Oscillator)和信号(Signal)在探测器上产生的直流电流分量,与时间无关。 I H ( t ) I_H(t) IH(t)是探测器输出的相干交流电流分量,是经过声光调制器、目标运动和环境干扰调制后输出的电流分量,这个相干电流是随时间变化的函数,称为中频电流,通常声光调制器的中频远大于目标的多普勒频移。
在这里, f A O M f_{AOM} fAOM是声光调制器的频率,通常远大于目标产生的多普勒频移 f d f_d fd。因此,输出的中频电流信号 I H ( t ) I_H(t) IH(t)将在中频 f A O M f_{AOM} fAOM附近震荡,这是系统获取的有效输出信号。
这样的模型适用于激光相干探测和多普勒测速等应用。这些公式提供了一个量化的方法来理解和分析系统的响应。
基于声光调制的外差干涉仪2
基于声光调制的双通道激光相干振动测量原理如图2.6所示。由激光光源产生的频率为 f 0 f_0 f0的光束经过分光镜后分为两束。其中一束通过光纤耦合器分为两路完全相同的测量光。这些测量光通过光纤环形器的1和2通道照射在待测振动物体的表面上,产生多普勒频移并散射。这时,散射光的频率 f 1 f_1 f1变为 f 0 − Δ f f_0 - \Delta f f0−Δf。这些散射光经过准直透镜耦合进光纤,并通过环形器的2和3通道形成测量光束。
另一路光束经过反光镜反射后进入声光调制器。声光调制器的调制频率 f M f_M fM为100.4MHz。经过声光调制后,衍射光束的频率 f 2 f_2 f2变为 f 0 + f M f_0 + f_M f0+fM。这个光束通过透镜耦合进光纤,并分为两路完全相同的光作为参考光束。
测量光束和参考光束一同照射在光电探测器的同一位置,在光电探测器表面发生光学混频,从而产生光电流。两束光的频率分别为 f 1 f_1 f1和 f 2 f_2 f2,电场强度分别由 E S R ( x , y ) E_{SR}(x, y) ESR(x,y)和 E L O ( x , y ) E_{LO}(x, y) ELO(x,y)表示。
E 1 = E 01 cos ( 2 π f 1 t + φ 1 ) E 2 = E 02 cos ( 2 π f 2 t + φ 2 ) \begin{array}{c}{{E_{1}=E_{01}\cos(2\pi f_{1}t+\varphi_{1})}}\\ {{\ }}\\ {{E_{2}=E_{02}\cos(2\pi f_{2}t+\varphi_{2})}}\end{array} E1=E01cos(2πf1t+φ1) E2=E02cos(2πf2t+φ2)
首先,设 E 01 E_{01} E01和 E 02 E_{02} E02分别为两光束的电场强度幅值, ϕ 1 \phi_1 ϕ1和 ϕ 2 \phi_2 ϕ2分别为两束光的初始相位。两束光的合成电场强度 E E E可以表示为:
E = E 01 cos ( 2 π f 1 t + ϕ 1 ) + E 02 cos ( 2 π f 2 t + ϕ 2 ) (2.37) E = E_{01} \cos(2\pi f_1 t + \phi_1) + E_{02} \cos(2\pi f_2 t + \phi_2) \quad \text{(2.37)} E=E01cos(2πf1t+ϕ1)+E02cos(2πf2t+ϕ2)(2.37)
由于光电探测器采用的是光电二极管,这是一种非线性光电器件,使其工作在第四象限接近线性区。由此,其光学混频表达式可以表示为:
I ( t ) = b 0 + b 1 E + b 2 E 2 I\left(t\right)=b_{0}+b_{1}E+b_{2}E^{2} I(t)=b0+b1E+b2E2
= b 0 + b 1 E 01 cos ( 2 π f 1 t + φ 1 ) + b 1 E 02 cos ( 2 π f 2 t + φ 2 ) + =b_{0}+b_{1}E_{01}\cos\left(2\pi f_1 t+\varphi_{1}\right)+b_{1}E_{02}\cos\left(2\pi f_2t+\varphi_{2}\right)+ =b0+b1E01cos(2πf1t+φ1)+b1E02cos(2πf2t+φ2)+
1 2 b 2 E 01 2 + 1 2 b 2 E 02 2 + 1 2 b 2 E 01 2 cos 2 ( 2 π f 1 t + φ 1 ) + 1 2 b 2 E 02 2 cos 2 ( 2 π f 2 t + φ 2 ) + \frac{1}{2}b_{2}E_{01}^{2}+\frac{1}{2}b_{2}E_{02}^{2}+\frac{1}{2}b_{2}E_{01}^{2}\cos^{2}\left(2\pi f_{1}t+\varphi_{1}\right)+\frac{1}{2}b_{2}E_{02}^{2}\cos^{2}\left(2\pi f_{2}t+\varphi_{2}\right)+ 21b2E012+21b2E022+21b2E012cos2(2πf1t+φ1)+21b2E022cos2(2πf2t+φ2)+
b 2 E 01 E o 2 cos [ 2 π ( f 1 + f 2 ) t + ( φ 1 + φ 2 ) ] + b 2 E o 1 E o 2 cos [ 2 π ( f 2 − f 1 ) t + ( φ 2 − φ 1 ) ] b_{2}E_{01}E_{\mathrm{o2}}\cos[2\pi\bigl(f_{1}+f_{2}\bigr)t+\bigl(\varphi_{1}+\varphi_{2}\bigr)\bigr]+b_{2}E_{\mathrm{o1}}E_{\mathrm{o2}}\cos\Bigl[2\pi\bigl(f_{2}-f_{1}\bigr)t+\bigl(\varphi_{2}-\varphi_{1}\bigr)\bigr] b2E01Eo2cos[2π(f1+f2)t+(φ1+φ2)]+b2Eo1Eo2cos[2π(f2−f1)t+(φ2−φ1)]
式中,前三项均为高频分量。只有第四项为低频分量,且与物体表面的状态有关。第四项的含义是φ2所代表的物体表面与φ1所代表的参考面之间的相对变化量。
b 1 b_1 b1和 b 2 b_2 b2为常数,与光电探测器的自身参数有关。直流分量可以通过电容滤除。
经选频放大器后,光电探测器的输出电流信号留下放大后的差频电压信号 U ( t ) U(t) U(t):
上面这句话没懂,输出电流信号留下放大后的差频电压信号,是如何做到的,公式又如何推导
U ( t ) = U 0 cos ( 2 π ( f M + Δ f ) t + Δ φ ) (2.39) U(t) = U_0 \cos(2\pi (f_M + \Delta f) t + \Delta\varphi) \quad \text{(2.39)} U(t)=U0cos(2π(fM+Δf)t+Δφ)(2.39)
通过调理电路,先将信号频率搬移到中频10.7MHz进行放大滤波处理,得到的中频信号 U I ( t ) U_I(t) UI(t)可以表示为:
U I ( t ) = U I cos ( 2 π ( f M − f L + Δ f ) t + Δ φ ) (2.40) U_I(t) = U_I \cos(2\pi (f_M - f_L + \Delta f) t + \Delta\varphi) \quad \text{(2.40)} UI(t)=UIcos(2π(fM−fL+Δf)t+Δφ)(2.40)
当物体振动时,振动速度 v ( t ) v(t) v(t)可以表示为:
v ( t ) = V 0 sin ( 2 π f t ) (2.41) v(t) = V_0 \sin(2\pi f t) \quad \text{(2.41)} v(t)=V0sin(2πft)(2.41)
综合以上所有信息,最终的输出信号
U
I
(
t
)
U_{I}(t)
UI(t)可以用以下方式表示:
U
I
(
t
)
=
U
I
cos
[
2
π
(
f
M
−
f
L
+
2
V
0
cos
θ
λ
sin
2
π
f
t
)
t
+
Δ
φ
]
U_{I}\bigl(t\bigr)=U_{I}\cos\Biggl[2\pi(f_{\mathrm{M}}\!-\!f_{\mathrm{L}}\!+\!\frac{2V_0\cos\theta}{\lambda}\!\sin2\pi f\!t)t+\Delta\varphi\Biggl]
UI(t)=UIcos[2π(fM−fL+λ2V0cosθsin2πft)t+Δφ]
这样的信号是一个典型的调频信号。由于多普勒频移载在10.7MHz的固定中频上,可以很容易确定频移的正负。
经检波电路解调后,得到多普勒信号 U D ( t ) U_D(t) UD(t):
U D ( t ) = U D cos ( 2 π Δ f t + Δ φ ) (2.43) U_D(t) = U_{D} \cos(2\pi \Delta f t + \Delta\varphi) \quad \text{(2.43)} UD(t)=UDcos(2πΔft+Δφ)(2.43)
通过信号采集系统将多普勒信号转换为数字量送入计算机,由数字信号处理模块可以精确测出多普勒频率 D f D_f Df的大小,进而得到多普勒频移 Δ f \Delta f Δf。基于这些信息,可以计算出待测物体的振动速度为:
v ( t ) = λ 2 c o s θ Δ f ( t ) (2.44) v(t) = \frac{\lambda}{2cosθ} \Delta f(t) \quad \text{(2.44)} v(t)=2cosθλΔf(t)(2.44)
其中, v ( t ) v(t) v(t)是振动速度, λ \lambda λ是激光的波长, Δ f \Delta f Δf是多普勒频移。
对 v ( t ) v(t) v(t)进行积分,可以得到待测物体在振动方向上的位移 X X X:
X ( t ) = ∫ v ( t ) d t = ∫ λ 2 cos θ Δ f ( t ) d t X(t) = \int v(t) \, dt = \int \frac{\lambda}{2\cos \theta} \Delta f(t) \, dt X(t)=∫v(t)dt=∫2cosθλΔf(t)dt
其中, θ \theta θ是与振动方向有关的角度。
对 v ( t ) v(t) v(t)进行微分,可得到待测物体在振动方向上的加速度 a a a:
a = d d t ( 2 cos ( θ ) Δ f λ 2 ) a = \frac{d}{dt} \left( 2 \cos(\theta) \Delta f \frac{\lambda}{2} \right) a=dtd(2cos(θ)Δf2λ)
或简化为:
a = cos ( θ ) d Δ f d t λ a = \cos(\theta) \frac{d \Delta f}{dt} \lambda a=cos(θ)dtdΔfλ
这样,我们就可以通过这一系列的公式,精确地测量待测物体在振动时的速度、位移和加速度。
其他
激光干涉仪为了提高测量精度会采用一些特殊技术:
稳频激光器、准直系统。。。
稳频激光器:测量的精度很大程度上取决于波长的精度;激光器尽可能实现单波长稳定输出。
激光器频率变化的主要原因:
(1)温度影响:任何材料的物体线性尺寸都随温度而变化;激光管所用的玻璃、金属支架的尺寸都随温度的变化而变化(一般满足热涨冷缩的原理),故引起频率的漂移。
(2)机械影响:外界的机械振动,如建筑物的震动、车辆通行和声响等都会引起腔的支架振动,使谐振腔的光学长度
发生变化,从而导致振荡频率的漂移。为了克服机械振动的影响,稳频激光器必须准备良好的防震措施。
(3)磁场影响:激光器谐振腔间隔器多采用殷钢材料,但殷钢的磁致伸缩性质可能引起腔长的变化。



























 4835
4835

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








