计算机视觉——SIFT算法之高斯金字塔

计算机视觉—SIFT算法之高斯金字塔

brycezou@163.com

1、高斯金字塔–>DoG金字塔

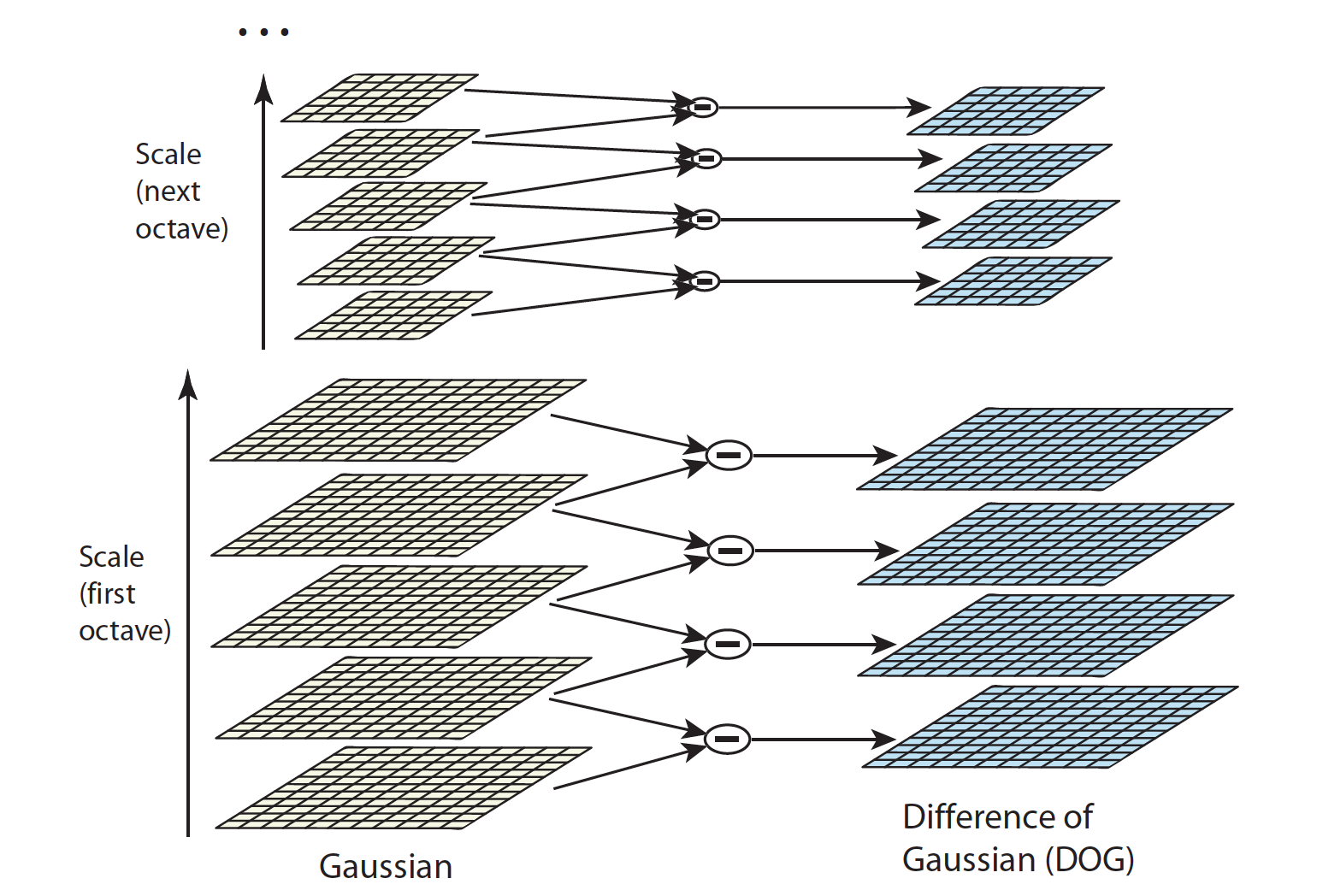
       在理论上，输入图像需要先分别与不同尺度的高斯核进行卷积，然后求两幅图像的差。而在实际中更为简单，如图所示，高斯金字塔相邻两层相减，便可以得到 $DoG$ 金字塔。这是因为，高斯金字塔每层中的多幅图像，原本就是通过对同一幅输入图像进行不同尺度的高斯卷积得来的。关于高斯金字塔的构造方法，请继续阅读下文。
$$D(x,y,\sigma)=(G(x,y,k\sigma)-G(x,y,\sigma))*I(x,y)$$

2、SIFT算法中的高斯金字塔

       图像金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，自底向上构成的塔状模型。原始图像为金字塔的第一层，每次降采样得到的新图像为金字塔的一层（每层一张图像）。

       SIFT算法中的高斯金字塔略有不同。为了让尺度体现其连续性，在简单下采样的基础上添加了多尺度的高斯滤波。一幅图像可以产生几组（Octave）图像，一组图像又包括几层（Interval）图像，并且组数和金字塔的层数相等。





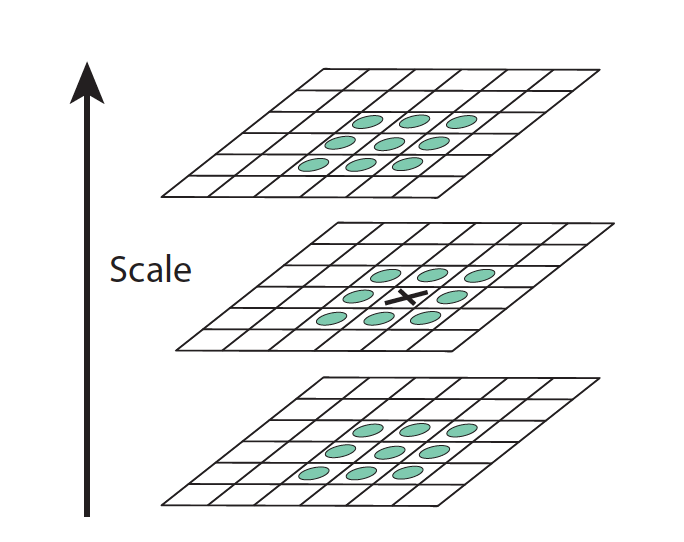
       为了在每组图像中检测 $S$ 个尺度的极值点， $DoG$ 金字塔每组需 $S+2$ 层图像，因为每组的第一层和最后一层图像上不能检测极值，如图；而 $DoG$ 金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需 $S+3$ 层图像，实际计算时 $S$ 通常在3到5之间。SIFT算法中生成高斯金字塔的规则如下：

       设高斯金字塔共包含 $O$ 组图像，每组图像有 $S+3$ 层，
$$O=\log_{2}(min\{M,N\})-3$$
其中， $M,N$分别为原始图像的行数和列数。

       设位于金字塔底的第1组的第1层图像，其高斯滤波的尺度为
$$\sigma(o=1,s=1)=\sigma_1^{(1)}$$
则位于第1组的其它层图像的高斯滤波尺度分别为


       $\sigma(o=1,s=2)=\sigma_2^{(1)}=k\sigma_1^{(1)}$

       $\sigma(o=1,s=3)=\sigma_3^{(1)}=k\sigma_2^{(1)}=k^2\sigma_1^{(1)}$

              $\cdots$

       $\sigma(o=1,s=S+3)=\sigma_{S+3}^{(1)}=k\sigma_{S+2}^{(1)}=\cdots=k^{S+2}\sigma_1^{(1)}$


同理，位于第2组的各层图像的高斯滤波尺度分别为


       $\sigma(o=2,s=1)=\sigma_1^{(2)}$

       $\sigma(o=2,s=2)=k\sigma_1^{(2)}$