Qt绘图：求圆和椭圆上任意角度点的坐标

龚建波

已于 2023-07-18 18:34:47 修改

阅读量9.3k

点赞数 5

分类专栏： Qt 略知一二文章标签：椭圆坐标圆坐标绘图 QPainter Qt

于 2020-07-20 23:56:32 首次发布

本文链接：https://blog.csdn.net/gongjianbo1992/article/details/107476030

版权

Qt 略知一二专栏收录该内容

91 篇文章 248 订阅

订阅专栏

（2021-02-11 之前把笛卡尔坐标的 x 和 y 标注反了，已修正）

（2023-07-18 之前把旋转矩阵坐标算错了，已修正）

0.圆相关公式

在笛卡尔坐标系上，一个标准的圆是这样的：

已知圆心坐标（x0，y0），半径 R，角度 a，则圆边上点（x'，y'）的坐标为：

C 的三角函数参数为弧度，转换如下：

角度转弧度： $radian =\frac{\pi \cdot angle}{180}$

弧度转角度： $angle =\frac{180 \cdot radian }{\pi}$

但我们知道，Qt 绘图是屏幕坐标系，起点在左上角，以右下角为正方向：

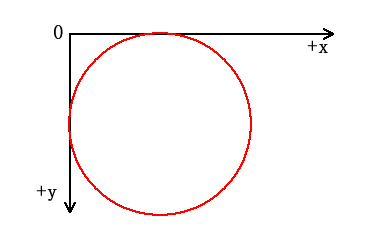
（可以把计算后的 y 取反来得到想要的效果）

void MainWindow::paintEvent(QPaintEvent *event)
{
    event->accept();

    QPainter painter(this);
    painter.setPen(QPen(Qt::red,2));
    //移动坐标中心点到窗口中心，默认左上角为起点，往右下为正方向
    painter.translate(width()/2,height()/2);
    //画一个圆，圆心为起点（上一步移动到的正中），半径100px
    const int R=100;
    painter.drawEllipse(QPoint(0,0),R,R);
    //计算45度角圆边上的点，角度需要转换为弧度
    const double a=qDegreesToRadians((double)45);
    const int x=0+R*cos(a);
    const int y=0+R*sin(a);
    //因为屏幕坐标系y轴正方向和笛卡尔坐标系相反，所以y取反就是我们要的结果了
    painter.drawLine(QPoint(0,0),QPoint(x,-y)); //y取反
}

运行结果：

1.椭圆相关公式

在笛卡尔坐标系上，一个标准的椭圆是这样的：

已知圆心坐标（x0，y0），横轴 A（长半轴），竖轴 B（短半轴），角度 a，则圆边上点（x'，y'）的坐标为：

椭圆半径：

（可以发现，与普通圆相比，不考虑椭圆角度的话只是半径变化了，其他部分是一样的）

void MainWindow::paintEvent(QPaintEvent *event)
{
    event->accept();

    QPainter painter(this);
    painter.setPen(QPen(Qt::red,2));
    //移动坐标中心点到窗口中心，默认左上角为起点，往右下为正方向
    painter.translate(width()/2,height()/2);
    //画一个圆，圆心为起点（上一步移动到的正中），半径100px
    const int A=150; //横轴
    const int B=100; //竖轴
    painter.drawEllipse(QPoint(0,0),A,B);
    //计算45度角圆边上的点，角度需要转换为弧度
    const double a=qDegreesToRadians((double)45);
    const int R=A*B/sqrt(pow(A*sin(a),2)+pow(B*cos(a),2)); //计算对应角度的半径
    const int x=0+R*cos(a);
    const int y=0+R*sin(a);
    //因为屏幕坐标系y轴正方向和笛卡尔坐标系相反，所以y取反就是我们要的结果了
    painter.drawLine(QPoint(0,0),QPoint(x,-y)); //y取反
}

运行结果：

2.旋转矩阵

上面的角度都是从右侧开始，椭圆也是标准椭圆，如果我们想旋转一定角度来绘制，就需要用到我们的旋转矩阵了。

（本节主要来自参考博客）

已知 A(x,y) ，求旋转 a 角度后的 B(x’,y’) 坐标：

在这里插入图片描述

公式推导：

在这里插入图片描述

根据矩阵乘法计算规则，可以推出：

在这里插入图片描述

操作流程：

把图形的各点平移，令旋转中心平移至原点；
乘以旋转矩阵；
再平移至原来的旋转中心。

在这里插入图片描述

我们将上面椭圆的代码改一下，逆时针旋转 45 度：


void MainWindow::paintEvent(QPaintEvent *event)
{
    event->accept();

    QPainter painter(this);
    painter.setPen(QPen(Qt::red,2));
    //移动坐标中心点到窗口中心，默认左上角为起点，往右下为正方向
    painter.translate(width()/2,height()/2);
    //画一个圆，圆心为起点（上一步移动到的正中），半径100px
    const int A=150; //横轴
    const int B=100; //竖轴
    painter.rotate(-45); //在屏幕坐标系，qpainter是顺时针转的
    painter.drawEllipse(QPoint(0,0),A,B);
    painter.rotate(45);

    //计算45度角圆边上的点，角度需要转换为弧度
    const double a=qDegreesToRadians((double)45);
    const int R=A*B/sqrt(pow(A*sin(a),2)+pow(B*cos(a),2)); //计算对应角度的半径
    const int x=0+R*cos(a);
    const int y=0+R*sin(a);
    //根据旋转矩阵计算
    const double a2=qDegreesToRadians((double)45);
    const int x2=x*cos(a2)-y*sin(a2);
    const int y2=x*sin(a2)+y*cos(a2);
    //因为屏幕坐标系y轴正方向和笛卡尔坐标系相反，所以y取反就是我们要的结果了
    painter.drawLine(QPoint(0,0),QPoint(x2,-y2)); //y取反
}

运行结果：

（第一次计算的角度坐标是计算标准椭圆下的位置，第二次是根据椭圆的旋转角度做旋转得到的坐标）

（本来就有 45 度，从右侧逆时针旋转，再旋转 45 度就成了垂直向上了）