简单易学的机器学习算法——SVD奇异值分解

最新推荐文章于 2024-05-16 11:19:15 发布

zhiyong_will

最新推荐文章于 2024-05-16 11:19:15 发布

阅读量3.5w

点赞数 6

分类专栏：机器学习，数据挖掘算法文章标签：机器学习奇异值分解 SVD

本文链接：https://blog.csdn.net/google19890102/article/details/27109235

版权

机器学习，数据挖掘算法专栏收录该内容

60 篇文章 496 订阅

订阅专栏

一、SVD奇异值分解的定义

假设 $M$ 是一个 $m\times n$ 的矩阵，如果存在一个分解：

$M=U\sum V^{T}$

其中 $U$ 为 $m\times m$ 的酉矩阵， $\sum$ 为 $m\times n$ 的半正定对角矩阵， $V^{T}$ 为 $V^$ 的共轭转置矩阵，且为 $n\times n$ 的酉矩阵。这样的分解称为 $M$ 的奇异值分解， $\sum$ 对角线上的元素称为奇异值， $U$ 称为左奇异矩阵， $V^{T}$ 称为右奇异矩阵。

二、SVD奇异值分解与特征值分解的关系

特征值分解与SVD奇异值分解的目的都是提取一个矩阵最重要的特征。然而，特征值分解只适用于方阵，而SVD奇异值分解适用于任意的矩阵，不一定是方阵。

$M^{T}M=\left ( U\sum V^{T} \right )^{T}U\sum V^{T} \right=V\left ( \sum \, ^T\sum \right )V^{T}$

$MM^T=U\sum V^{T}\left ( U\sum V^{T} \right )^{T} \right=U\left ( \sum \sum \, ^T \right )U^{T}$

这里， $M^TM$ 和 $MM^T$ 是方阵， $U^TU$ 和 $V^TV$ 为单位矩阵， $V^{T}$ 为 $M^TM$ 的特征向量， $U$ 为 $MM^T$ 的特征向量。 $M^TM$ 和 $MM^T$ 的特征值为 $M$ 的奇异值的平方。

三、SVD奇异值分解的作用和意义

奇异值分解最大的作用就是数据的降维，当然，还有其他很多的作用，这里主要讨论数据的降维，对于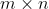 $m\times n$ 的矩阵 $M$ ，进行奇异值分解

$M_{m\times n}=U_{m\times m}\sum \, _{m\times n}V^T_{n\times n}$

取其前 $r$ 个非零奇异值，可以还原原来的矩阵 $M$ ，即前 $r$ 个非零奇异值对应的奇异向量代表了矩阵 $M$ 的主要特征。可以表示为

$M_{m\times n}\approx U_{m\times r}\sum \, _{r\times r}V^T_{r\times n}$

五、实验的仿真

我们在手写体上做实验，原始矩阵为

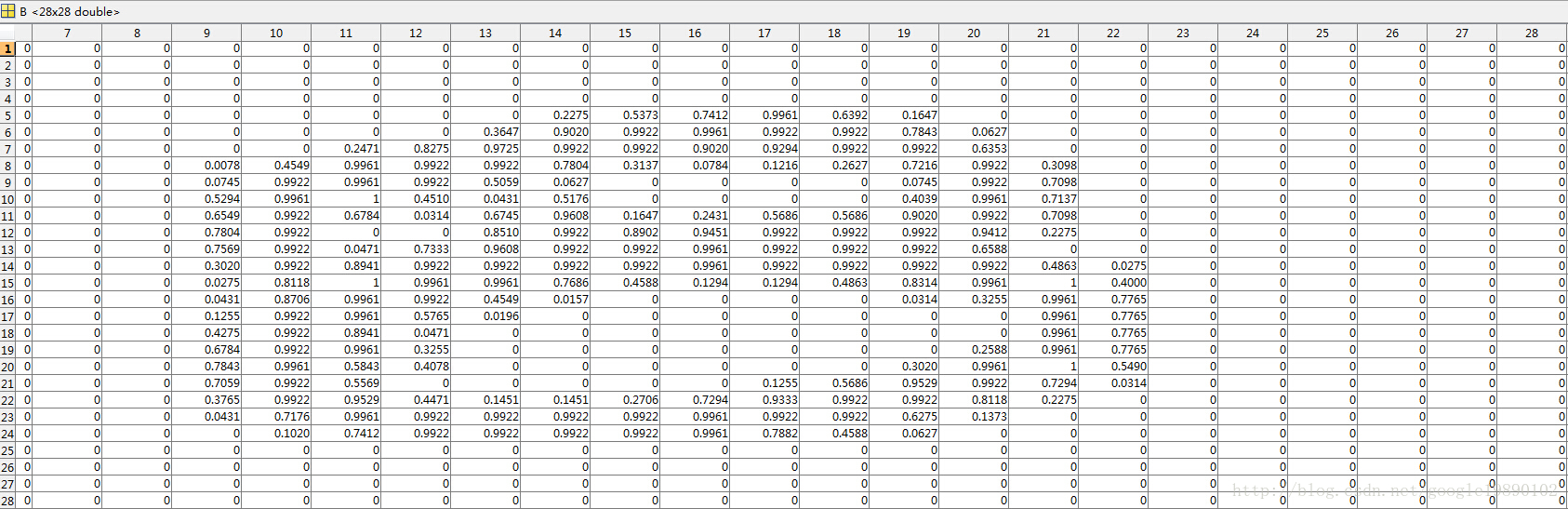
原始矩阵

对应的图像为

对应图像

经过SVD分解后的奇异值矩阵为

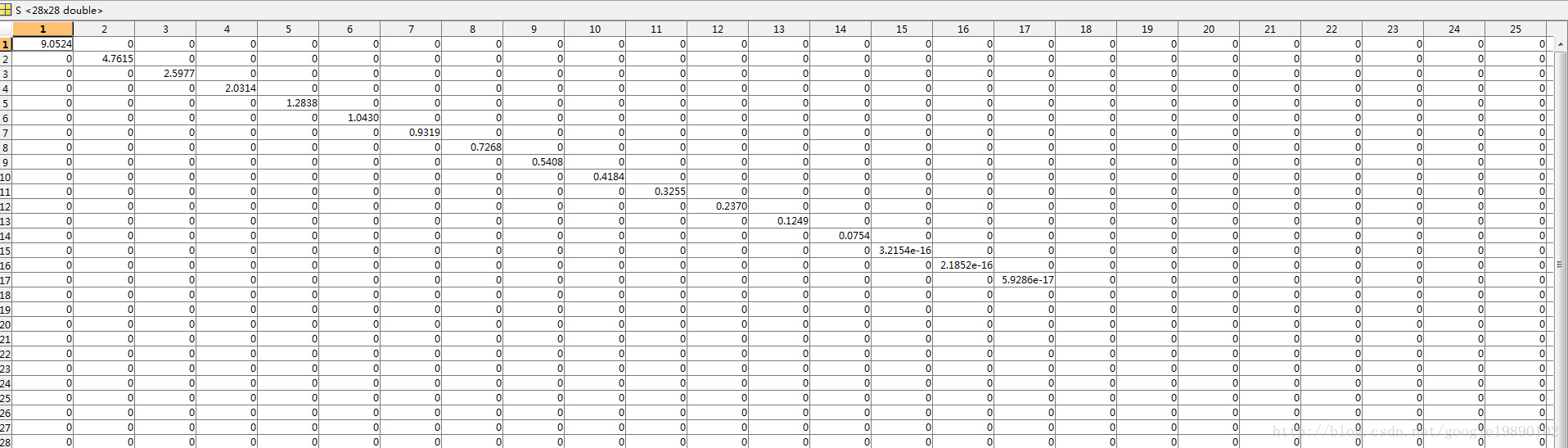
部分奇异值矩阵

取前14个非零奇异值

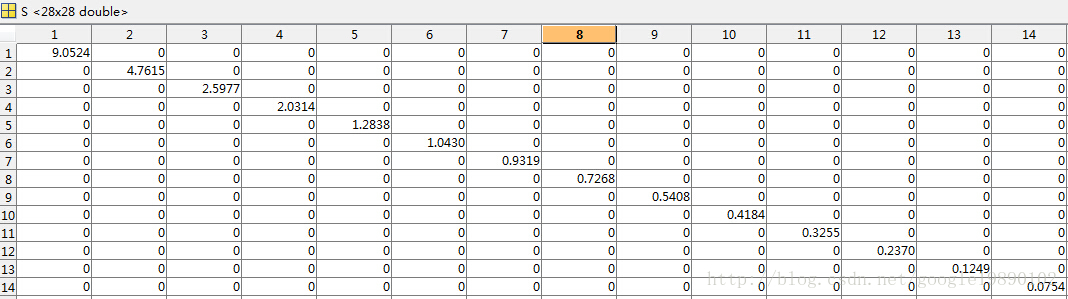
前14个非零奇异值

还原原始矩阵B，还原后的图像为

还原后的图像

对比图像

MATLAB代码

%% 测试奇异值分解过程
load data.mat;%该文件是做好的一个手写体的图片
B = zeros(28,28);%将行向量重新转换成原始的图片

for i = 1:28
    j = 28*(i-1)+1;
    B(i,:) = A(1,j:j+27);
end

%进行奇异值分解
[U S V] = svd(B);

%选取前面14个非零奇异值
for i = 1:14
    for j = 1:14
        S_1(i,j) = S(i,j);
    end
end

%左奇异矩阵
for i = 1:28
    for j = 1:14
        U_1(i,j) = U(i,j);
    end
end

%右奇异矩阵
for i = 1:28
    for j = 1:14
        V_1(i,j) = V(i,j);
    end
end

B_1 = U_1*S_1*V_1';

%同时输出两个图片
subplot(121);imshow(B);
subplot(122);imshow(B_1);