【博弈论】【第三讲】例题：沙滩博弈

【例题】

A、B两智能体(agent)在长度为1的直线区域上销售相同品种、相同价格的冷饮，游客均匀分布在海滩上且就近购买1单位的冷饮。证明:战略组合$s^{\ast }=\left(\frac{1}{2},\frac{1}{2}\right)$是该智能体博弈的唯一纯战略纳什均衡。

【解】

1.首先清楚博弈论三要素：

• 参与者集合
• 参与人的战略集合
• 列出支付函数

参与者集合就是$S_1$和$S_2$，而参与者的战略集合就都是在0与1之间：$S_1=S_2=[0,1]$，画在同一个数轴中的关系可见下图：

为了更清楚的表现$S_1$与$S_2$之间的战略关系，我们可以用二维图像来表现：

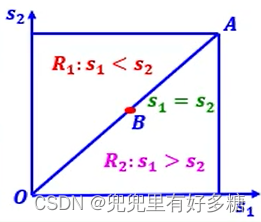
R 1 = { ( s 1 , s 2 ) ∣ s 1 < s 2 } R 2 = { ( s 1 , s 2 ) ∣ s 1 > s 2 } \begin{aligned} & R_1=\left\{\left(s_1, s_2\right) \mid s_1<s_2\right\} \\ & R_2=\left\{\left(s_1, s_2\right) \mid s_1>s_2\right\} \end{aligned} ​R1​={(s1​,s2​)∣s1​<s2​}R2​={(s1​,s2​)∣s1​>s2​}​
那么支付函数怎么写呢？
在图一中，我们可以知道：在$[0,S_1]$范围内，顾客会买$S_1$，在$[S_2，1]$区间内，顾客会买$S_2$，而在$[S_1,S_2]$之间的时候，在中点左边顾客会买$S_1$，中点右边顾客会买$S_2$。
所以可得到如下的支付函数：
$$u_1\left(s_1,s_2\right)=\{\begin{array}{l}\frac{s_1+s_2}{2},s_1<s_2\\ \\ 1/2,s_1=s_2\\ \\ 1-\frac{s_1+s_2}{2},s_1>s_2\end{array}$$
$$u_2\left(s_1,s_2\right)=\{\begin{array}{l}1-\frac{s_1+s_2}{2},s_1<s_2\\ \\ 1/2,s_1=s_2\\ \\ \frac{s_1+s_2}{2},s_1>s_2\end{array}$$

2.明确博弈三要素之后开始进行证明

我们要证明的是在$S_1<S_2$,$S_1>S_2$,以及$S_1=S_2$但不等于$\frac{1}{2}$的时候均不是纳什均衡。

证明$S_1<S_2$处不存在纳什均衡：
此处我们采取反证法，假设在$S_1<S_2$时存在纳什均衡。
也就是上面图二中$R_1$所示的区域。
所以即假设：在$R_1$中存在纳什均衡，设为$s^{\ast }$。则$s^{\ast }=(s_1^{\ast },s_2^{\ast })$，且$s_1^{\ast }<s_2^{\ast }$。
之后我们假设存在一个任意小的正整数$\epsilon >0$,使得$s_1^{\prime }=s_1{}^{\ast }+\epsilon <s_2{}^{\ast }$

则根据支付函数有：
$$u_1\left(s_1^{\prime },s_2^{\ast }\right)=\frac{s_1^{\prime }+s_2^{\ast }}{2}=\frac{s_1^{\ast }+\epsilon +s_2^{\ast }}{2}$$
$$u_1\left(s_1^{\ast },s_2^{\ast }\right)=\frac{s_1^{\ast }+s_2^{\ast }}{2}<\frac{s_1^{\ast }+\epsilon +s_2^{\ast }}{2}=u_1\left(s_1^{\prime },s_2^{\ast }\right)$$
所以我们可以明显观察到，$u_1(s_1^{\ast }，s_2^{\ast })$要小于$u_1(s_1^{\prime }，s_2^{\ast })$,所以$s_1$有向右移动的趋势，也即：$\epsilon$越大，$s_1$所获得的收益越大，所以$s_1$一定会向右移。则不满足纳什均衡定义。

纳什均衡定义是：如果$s_1^{\ast }$和$s_2^{\ast }$是纳什均衡，那每个参与者对对方都是最优反应，他不愿单独改变战略。
但是在这里，$s_1$单独改变战略会对他自己有更有利的影响，所以她当然愿意改变，所以不满足纳什均衡的要求。

证明$S_1>S_2$处不存在纳什均衡：
还是使用反证法，假设在$R_2$区域中存在纳什均衡，设纳什均衡的状态分别为$(s_1^{\ast },s_2^{\ast })$，则有：$s_1^{\ast }<s_2^{\ast }$.
同样的，假设有一个无穷小的正整数$\delta >0$，使得满足$s_1^{\prime }=S_1{}_1-\delta >s^{\ast }{}_2$，关系图如下所示：

那么根据支付函数有以下两个式子：
$$u_1\left(s_1^{\prime },s_2^{\ast }\right)=1-\frac{s_1^{\prime }+s_2^{\ast }}{2}=1-\frac{s_1^{\ast }-\delta +s_2^{\ast }}{2}$$
$$u_1\left(s_1^{\ast },s_2^{\ast }\right)=1-\frac{s_1^{\ast }+s_2^{\ast }}{2}<1-\frac{s_1^{\ast }-\delta +s_2^{\ast }}{2}=u_1\left(s_1^{\prime },s_2^{\ast }\right)$$
同理可得，$s_1$对$s_2$并不是最优反应。

证明$S_1=S_2$但小于$\frac{1}{2}$处不存在纳什均衡：
假设这个区域中存在纳什均衡$(s_1^{\ast },s_2^{\ast })$，且处于小于$\frac{1}{2}$的区域，就有：$$s{}_2^{\ast }=s_1^{\ast }<1/2$$
假设有一个无穷小的正整数$\theta >0$，使得式子满足：
$$s_1^{\prime }=s_1{}^{\ast }+\theta <1/2$$
则根据支付函数有：
$$\begin{array}{rl}& u_1\left(s_1^{\prime },s_2^{\ast }\right)=1-\frac{s_1^{\prime }+s_2{}^{\ast }}{2}=1-\frac{s_1^{\ast }+\theta +s_2^{\ast }}{2}=1-s_1^{\ast }-\frac{\theta }{2}\\ & =1-s_1^{\ast }-\theta +\frac{\theta }{2}=1-\left(s_1^{\ast }+\theta \right)+\frac{\theta }{2}>\frac{1}{2}+\frac{\theta }{2}>\frac{1}{2}=u_1\left(s_1{}^{\ast },s_2{}^{\ast }\right)\end{array}$$
根据上式同理可得，该关系不满足纳什均衡的定义，所以证明该区间不存在纳什均衡。

证明$S_1=S_2$但大于$\frac{1}{2}$处不存在纳什均衡：
选取一个正整数$\alpha$，使得其满足：$0<\alpha \le \frac{1}{2}$，让$s_1^{\prime }=s_1^{\ast }-\alpha =\frac{1}{2}-\alpha$,则有支付函数如下：
$$\begin{array}{rl}& u_1\left(s_1^{\prime },s_2^{\ast }\right)=\frac{s_1^{\prime }+s_2^{\ast }}{2}=\frac{1/2-a+1/2}{2}=1/2-a/2\\ & <u_1\left(s_1^{\ast },s_2^{\ast }\right)=1/2\end{array}$$

再让$s_1^{\prime }=s_1^{\ast }+\alpha =\frac{1}{2}+\alpha$，这时$s_1^{\prime }>s_1^{\ast }=s_2^{\ast }$，这时发现计算支付函数发现仍然是不如1/2处的大：
$$\begin{array}{rl}& u_1\left(s_1^{\prime },s_2^{\ast }\right)=1-\frac{s_1^{\prime }+s_2^{\ast }}{2}=1-\frac{1/2+a+1/2}{2}=1/2-a/2\\ & <u_1\left(s_1{\ast }_1,s_2{\ast }_2\right)=1/2\end{array}$$
综上所述，问题得证

【下面有一道类似的题目可以练习一下】

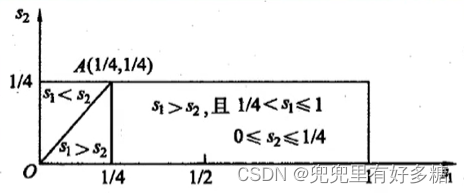
设出售相同商品的商店1、2在长度为1的街道上同时选择各自的位置。其中A的战略空间为$S_1=[0,1]$，B的战略空间为$S_2=[0,1/4]$.假设消费者均匀分布在该条街道上，每个消费者就近购买1单位的商品。是分析该博弈是否存在纳什均衡并加以证明。