【深度学习】02-02-类神经网络训练不起来怎么办?(局部最小值local minima & 鞍点saddle point)-李宏毅老师21&22深度学习课程笔记

总结

本节讨论：Optimization的时候，怎么把gradient descent做得更好？
当Gradient值为0时，使用 Hessian矩阵特征值正负，判断是saddle point还是local minima。
如果是local minima，现在已经达到了最优。
如果是saddle point，根据hessian判断参数的更新方向，继续更新。

如何判断Optimization是否失败？- 损失值较大&与其他模型相比效果不好

现在我们要讲的是Optimization的部分，等下我们要讲的东西基本上跟Overfitting没有什么太大的关联，我们只讨论Optimization的时候，怎么把gradient descent做得更好，那为什么Optimization会失败呢？

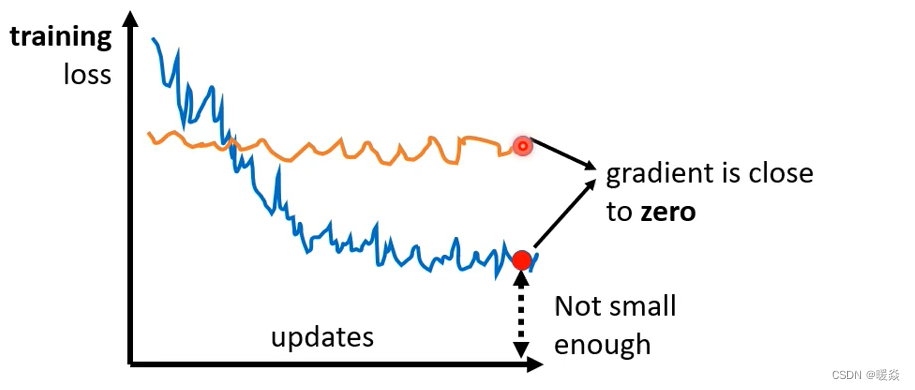
如上图蓝色线所示，你常常在做Optimization的时候会发现，随着你的参数不断的update，你的training的loss不会再下降，但是你对这个loss仍然不满意，你可以把deep的network跟linear的model或shallow network 比较，发现说它没有做得更好，所以你觉得deep network没有发挥它完整的力量，所以Optimization显然是有问题的。

如上图黄色线所示，有时候你会甚至发现，一开始你的model就train不起来，一开始你不管怎么update你的参数，你的loss通通都掉不下去。

为什么Optimization会失败？- Saddle Point & Local Minima

那这个时候到底发生了什么事情呢？

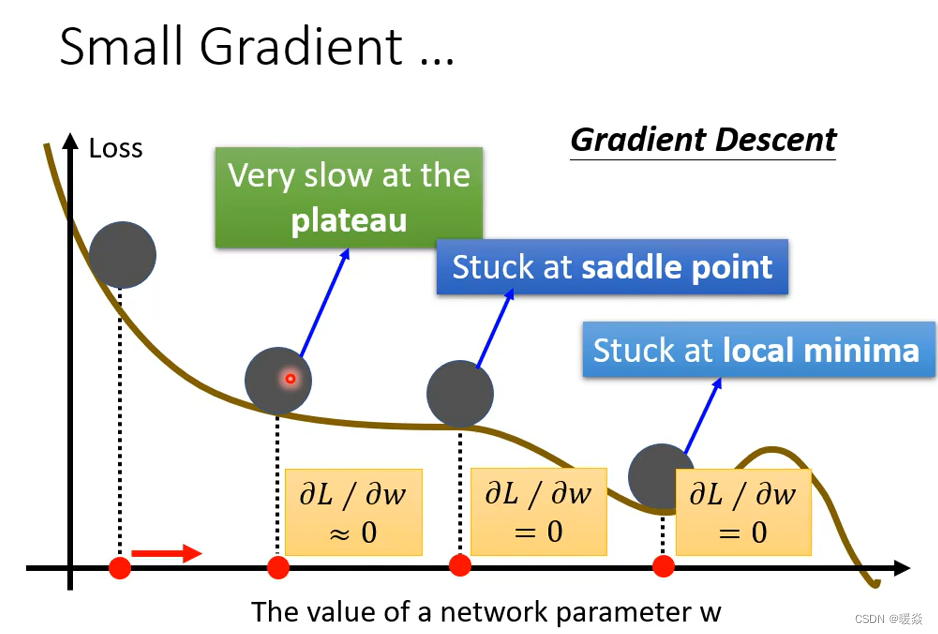
过去常见的一个猜想，是因为我们现在走到了一个地方，这个地方参数对loss的微分为零，当你的参数对loss微分为零的时候，gradient descent就没有办法再update参数了，这个时候training就停下来了，loss当然就不会再下降了。

​讲到gradient为零的时候，大家通常脑海中最先浮现的，可能就是local minima，所以常有人说做deep learning，用gradient descent会卡在local minima，然后因为gradient descent不work，所以deep learning不work。​但是如果有一天你要写deep learning相关paper的时候，你千万不要讲卡在local minima这种事情，别人会觉得你非常没有水平，为什么？

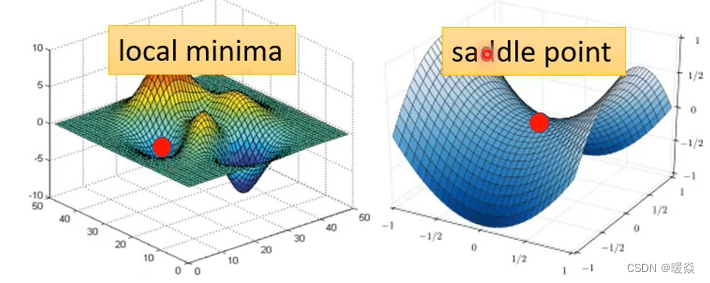
因为不是只有local minima的gradient是零，还有其他可能会让gradient是零，比如说 saddle point。所谓的saddle point就是gradient是零，但是不是local minima，也不是local maxima的地方，像上图右边这个例子里面红色的这个点，它在左右这个方向是比较高的，前后这个方向是比较低的，它像是一个马鞍的形状，所以叫做saddle point（鞍点）。像saddle point这种地方，它也是gradient为零，但它不是local minima，那像这种gradient为零的点，统称为critical point，所以你可以说你的loss，没有办法再下降，也许是因为卡在了critical point，但你不能说是卡在local minima，因为saddle point也是微分为零的点。但是今天如果你发现你的gradient，真的很靠近零，卡在了某个critical point，我们有没有办法知道，到底是local minima，还是saddle point？其实是有办法的。

为什么想要知道是卡在local minima还是saddle point？

因为如果是卡在local minima，那可能就没有路可以走了，因为四周都比较高，你现在所在的位置已经是最低的点，loss最低的点了，往四周走loss都会比较高，你不知道怎么走到其他的地方去。但saddle point就没有这个问题，如果你今天是卡在saddle point的话，saddle point旁边还是有路可以走的，还可以让你的loss更低的，你只要逃离saddle point，你就有可能让你的loss更低。

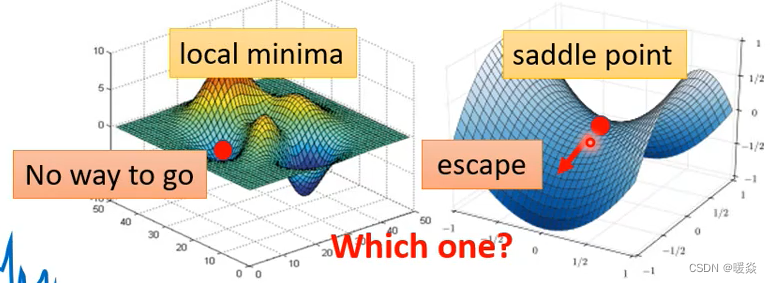
​所以鉴别我们走到critical point的时候，到底是local minima还是saddle point，是一个值得去探讨的问题，那怎么知道一个critical point，到底是属于local minima还是saddle point呢？

如何判断 Local Minima or Saddle Point? - Hessian & 特征值正负

这边需要用到一点数学，以下这段其实没有很难的数学，就只是微积分跟线性代数，但如果你没有听懂的话，以下这段skip掉是没有关系的。

​那怎么知道说一个点，到底是local minima还是saddle point呢？

你要知道我们loss function的形状，可是我们怎么知道loss function的形状呢，network本身很复杂，算出来的loss function显然也很复杂。

但是如果给定某一组参数，比如说蓝色的这个θ’，在θ’附近的loss function是有办法被写出来的，它写出来就是右侧这个样子。所以这个L(θ)完整的样子写不出来，但是它在θ’附近可以用这个式子来表示它，这个式子是Tayler Series Appoximation泰勒级数展开，这个假设你在微积分的时候已经学过了，所以我就不会细讲这一串是怎么来的，但我们就只讲一下它的概念，这一串里面包含什么东西呢?

• 第一项是L(θ’)，就告诉我们说，当θ跟θ’很近的时候，L(θ)应该跟L(θ’)还蛮靠近的。
• 第二项（上图绿色框）是(θ-θ’)^T*g，其中g是一个矢量，这个g就是我们的gradient，我们用绿色的g来代表gradient，这个gradient会来弥补θ’跟θ之间的差距。虽然说θ’跟θ应该很接近，但是中间还是有一些差距的。那这个差距，用这个gradient来表示他们之间的差距，有时候gradient会写成∇L(θ’)，这个地方的g是一个矢量，它的第i个component，就是θ的第i个component对L的微分，光是看g还是没有办法完整的描述L(θ)，还要看第三项。
• 第三项（上图红色框）跟Hessian有关。这个H叫做Hessian矩阵，这个第三项是(θ-θ’)^TH(θ-θ’)，所以第三项会再补足，再加上gradient以后与真正的L(θ)之间的差距。H里面放的是L的二次微分，它第i个row，第j个column的值，就是把θ的第i个component对L作微分，再把θ的第j个component，对L作微分，做两次微分以后的结果就是这个H_ij。

如果这边你觉得有点听不太懂的话，也没有关系。反正你就记得这个L(θ)的loss function，这个error surface在θ’附近可以写成这个样子，这个式子跟gradient和hessian两个东西有关系，gradient就是一次微分，hessian就是里面有二次微分的项目。

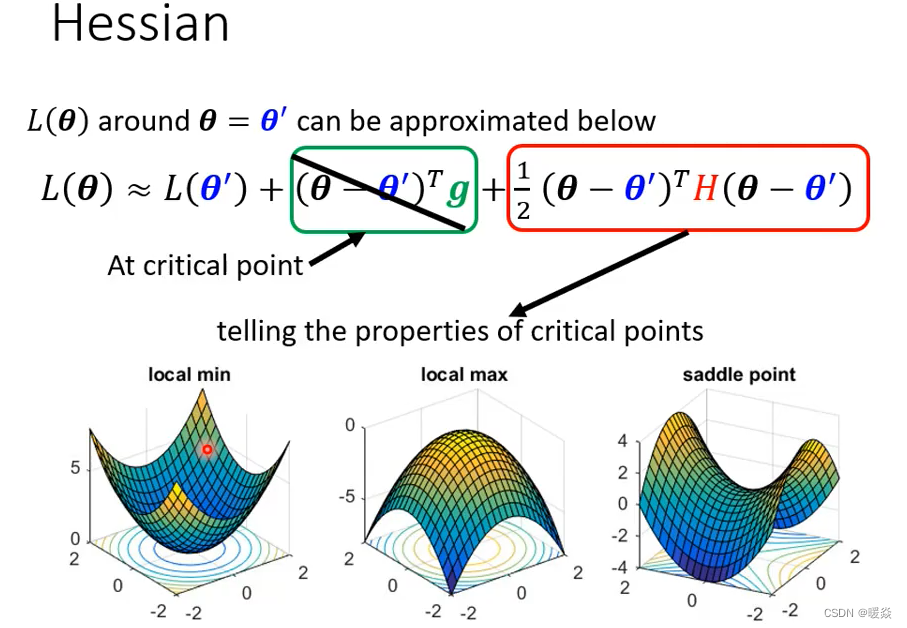
那如果我们走到了一个critical point，意味着gradient为零。

如上图，g是一个zero vector，绿色的这一项完全都不见了，只剩下红色的这一项。所以当在critical point的时候，这个loss function可以被近似为L(θ’)加上红色的这一项。可以根据红色的这一项来判断在θ’附近的error surface到底长什么样子，知道error surface长什么样子，就可以判断 θ’它是local minima、local maxima还是saddle point。

那我们就来看一下怎么根据Hessian，怎么根据红色的这一项，来判断θ’附近的地貌？。

现在为了符号方便起见，把(θ-θ’)用v这个矢量来表示。分析H矩阵时，主要有如下三种情况：

• ①如果对任何可能的v，v^THv都大于零，也就是说现在θ不管代任何值，v可以是任何的v，红色框里面通通都大于零，那意味着说 L(θ)大于L(θ’)。L(θ)不管代多少，只要在θ’附近，L(θ)都大于L(θ’)，代表L(θ’)是附近的一个最低点，所以它是local minima。

• ②如果今天反过来说，对所有的v而言，v^THv都小于零，θ不管代什么值，红色框框里面都小于零，意味着L(θ)小于L(θ’)，代表L(θ’)是附近最高的一个点，所以它是local maxima。

• ③第三个可能是假设，v^THv有时候大于零、有时候小于零，你代不同的v进去，代不同的θ进去，红色这个框框里面有时候大于零，有时候小于零，意味着说在θ’附近有时候L(θ)大于L(θ’) 有时候L(θ)小于L(θ’)，在L(θ’)附近有些地方高、有些地方低，这意味着这是一个saddle point。

​但是你这边是说我们要代所有的v，看v^THv是大于零还是小于零。我们怎么有可能把所有的v，都拿来试试看呢，所以有一个更简便的方法，去确认说这一个条件会不会发生。

这个就直接告诉你结论，线性代数理论上是有教过这件事情的，如果今天对所有的v而言，v^THv都大于零，那这种矩阵叫做正定矩阵（positive definite ），它所有的eigen value特征值都是正的。所以如果你今天算出一个hessian，你不需要把它跟所有的v都乘起来，你只要去直接看这个H的eigen value，如果你发现：

• ①Hessian矩阵正定，所有eigen value都是正的，那就代表说这个条件成立，v^THv会大于零，代表说是一个local minima。所以你从hessian metric可以看出，它是不是local minima，你只要算出hessian metric以后，看它的eigen value发现都是正的，它就是local minima。

• ②Hessian矩阵负定，对所有的v而言v^THv小于零，那H是negative definite，代表所有eigen value都是负的，就保证他是local maxima。

• ③Hessian矩阵不定，那如果eigen value有正有负，那就代表是saddle point。

总之，那假设在这里你没有听得很懂的话，你就可以记得结论——你只要算出hessian矩阵，这个矩阵如果它所有的eigen value都是正的，那就代表我们现在在local minima，如果它有正有负，就代表在saddle point。

那如果刚才讲的，你觉得你没有听得很懂的话，我们这边举一个例子。

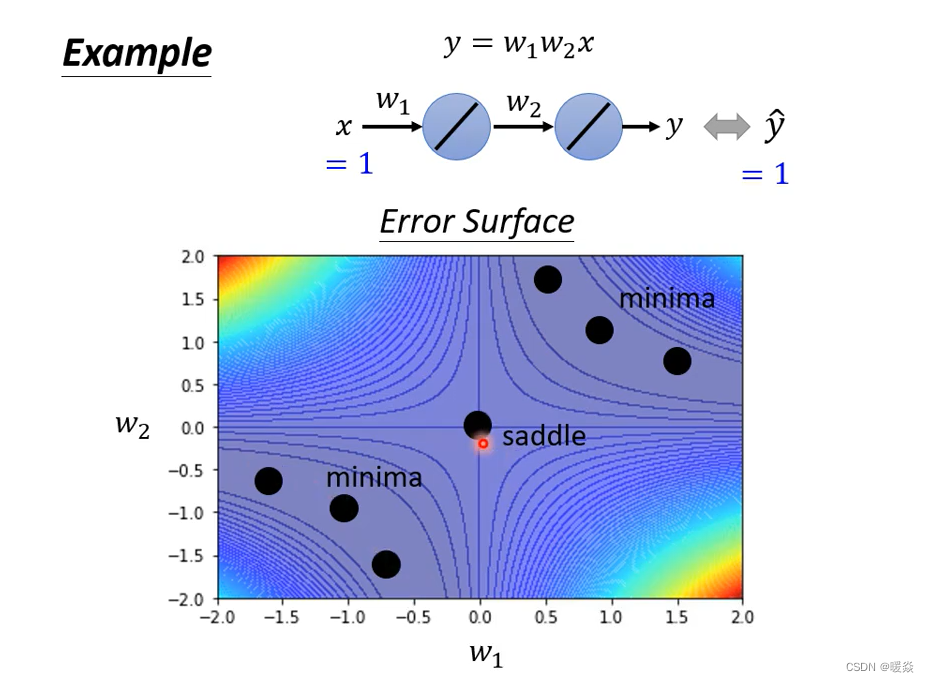
四个角落loss是高的，那这个图上你可以看出来说,有一些critical point，这个黑点的地方(0,0)，原点的地方是critical point，然后事实上，右上三个黑点也是一排critical point，左下三个点也是一排critical point。

图里的线是等高线即每条线loss相等，可以把颜色当做loss的值，一个新的维度，想象一下 3D的图，冷色 loss 为谷，暖色 loss 为峰。

现在假设如果不暴力所有可能的loss，如果要直接算说一个点，是local minima，还是saddle point的话，怎么计算呢？

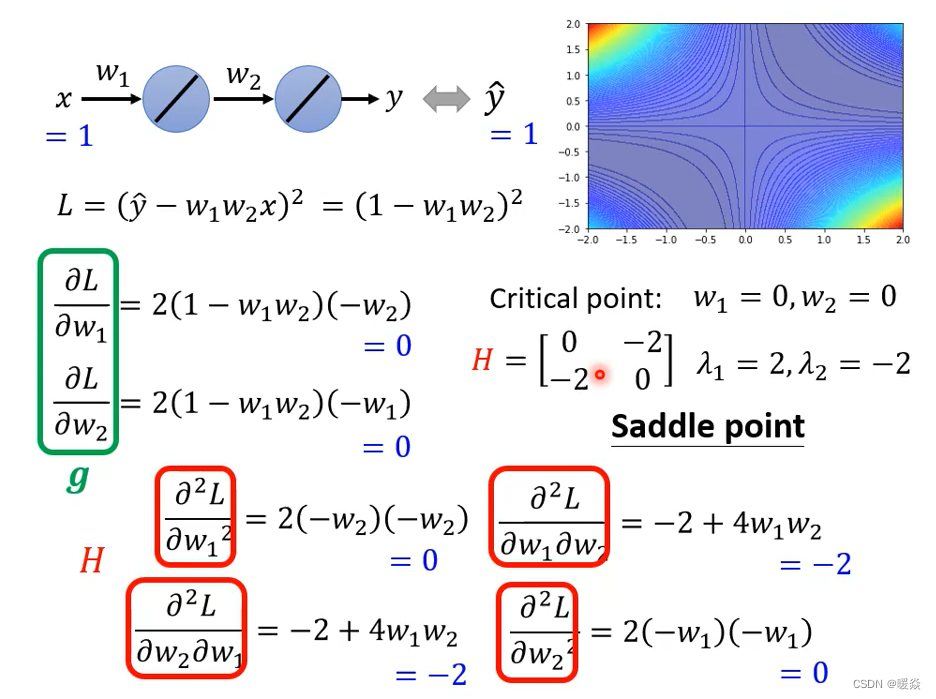
当然 我们刚才已经暴力所有可能的w₁ w₂了,所以你已经知道说,它显然是一个saddle point,但是现在假设还没有暴力所有可能的loss,所以我们要看看能不能够用H,用Hessian看出它是什么样的critical point,那怎么算出这个H呢

H它是一个矩阵,这个矩阵里面元素就是L的二次微分,所以这个矩阵里面第一个row,第一个coloumn的位置,就是w₁对L微分两次,第一个row 第二个coloumn的位置,就是先用w₂对L作微分,再用w₁对L作微分,然后这边就是w₁对L作微分,w₂对L作微分,然后w₂对L微分两次,这四个值组合起来,就是我们的hessian,那这个hessian的值是多少呢。

这个hessian告诉我们,它是local minima,还是saddle point呢,那你就要看这个矩阵的eigen value,算一下发现,这个矩阵有两个eigen value，2跟-2，eigen value有正有负,代表该点是 saddle point 。

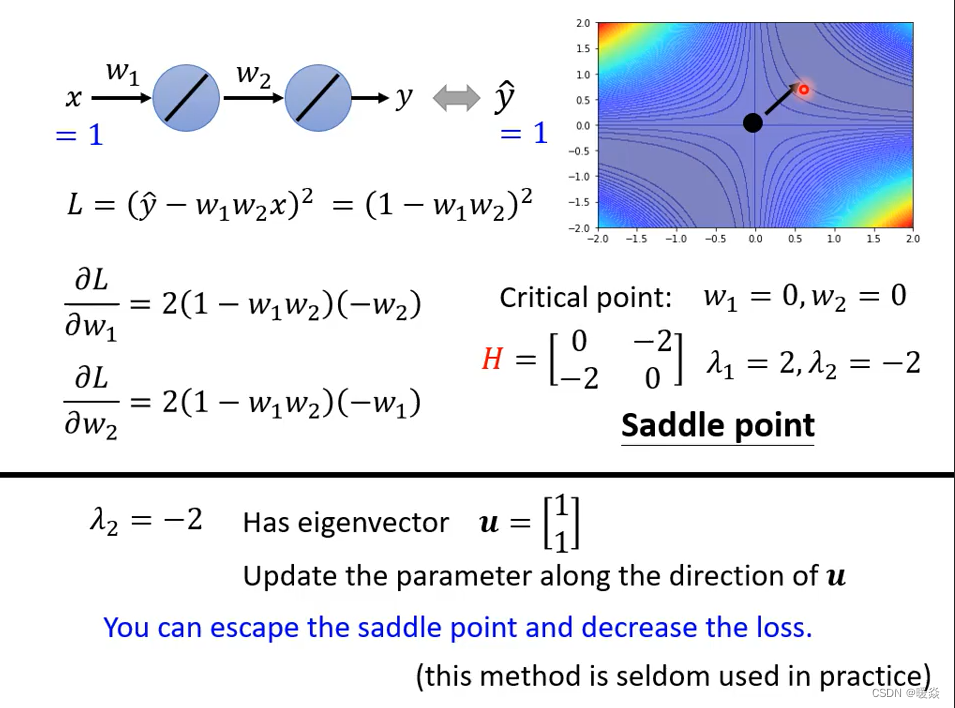
从 Hessian 矩阵 看出参数更新方向 - 负特征值对应特征向量方向

以前，参数的更新方向看 Gradient，当卡在saddle point时，Gradient消失，可以继续从 Hessian 看出参数更新方向。

取负特征值对应的特征向量方向，作为参数更新方向。

例如，在上面的例子中，eigen vector 为-2时，特征向量为u，则参数的更新方向即为沿着u的方向。

为什么要取负特征值对应的特征向量方向为梯度更新方向？- $L(\theta )=L({\theta }^{\prime })+\lambda ||u|{|}^2$

因为$u^{T}Hu=\lambda ||u|{|}^2$，因为$||u|{|}^2>0$，当$\lambda <0$时，$u^{T}Hu=\lambda ||u|{|}^2<0$，所以$L(\theta )<L({\theta }^{\prime })$，此时从${\theta }^{\prime }$更新到$\theta$梯度会下降，有$\theta ={\theta }^{\prime }+u$。

因为计算量很大，在实际使用中，很少有人用该方法逃离 saddle point，需要计算出二次微分，之后计算出 Hessian矩阵的特征值及其对应的特征向量。之后，还会介绍其他更简单的方法逃离 saddle point。

Saddle Point Vs Local Minima 哪个更常见？- Saddle Point

saddle point 和 local minima 哪个更常见？

低维空间的 local minima ，有可能在高维空间中是 saddle point，维度越高，可以走的路越多。实际使用中，参数都是成千上万，在很高的维度，所以 saddle point 更常见。

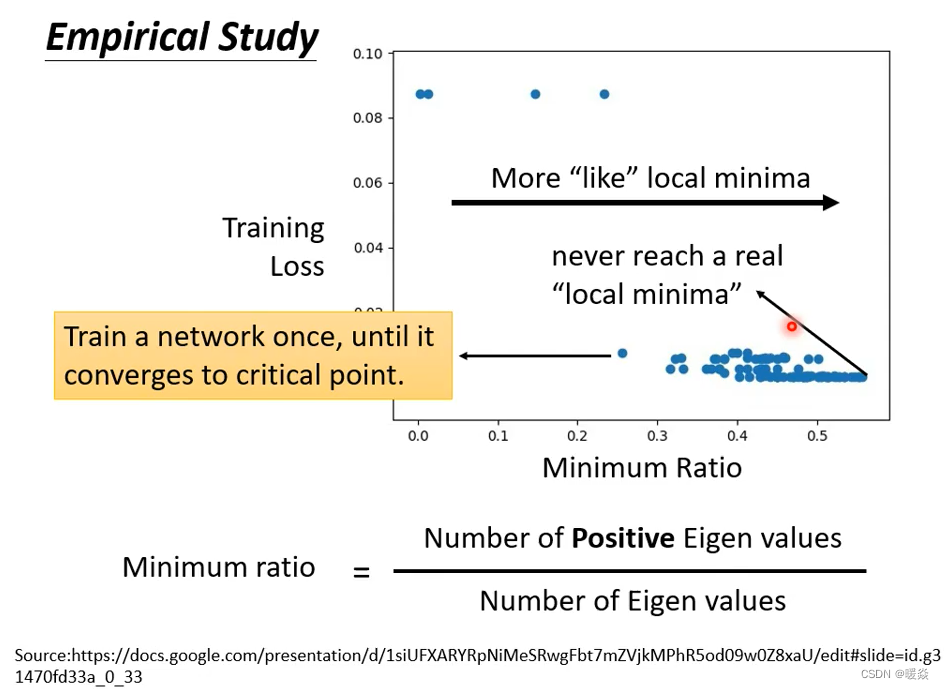
这是训练某一个network的结果，每一个点代表训练那个network训练完之后把它的Hessian拿出来进行计算。所以这边的每一个点都代表一个network。

我们训练某一个network，然后把它不断的进行训练，直到到gradient很小，卡在critical point。然后把那组参数出来分析，看看它是saddle point还是local minima。

纵轴代表training的时候的loss，就是卡住的那个loss。很多时候，你的loss在还很高的时候就训练不动了，就卡在critical point；那很多时候loss可以降得很低才卡在critical point，这是纵轴的部分。

横轴的部分是minimum ratio（最小比率）。minimum ratio是eigen value是正数的数目比eigen value的总数目，又如果所有的eigen value都是正的，代表我们今天的critical point是local minima；如果有正有负代表saddle point。那在实作上你会发现几乎找不到所有eigen value都是正的critical point。

所以虽然在这个图上，越往右代表我们的critical point越像local minima。但是它们都没有真的变成local minima。就算是在最极端的状况（最右边的点）,我们仍然有一半的case中eigen value是负的。这一半case的eigen value是正的，就代表在所有的维度裡面有一半的路，这一半的路如果要让loss上升，还有一半的路可以让loss下降。

所以从经验上看起来其实local minima并没有那么常见。多数的时候你觉得你train到一个地方，你gradient真的很小，然后所以你的参数不再update了，往是因为你卡在了一个saddle point。