本文参考项亮的《推荐系统实践》中基于用户的协同过滤算法内容。因其中代码实现部分只有片段,又因本人初学,对python还不是很精通,难免头大。故自己实现了其中的代码,将整个过程走了一遍。
1. 过程简述
a. 首先我们因该先找到和目标用户兴趣相似的用户集合。简单来说,如果A是目标用户(待推荐用户),那么我们要先找到和A兴趣差不多的一群人(例如B,C,D)。我认为B,C,D喜欢的商品,A也很有可能喜欢。(臭味相投嘛)
b. 找到集合中用户喜欢的,且目标用户没有听说过的物品推荐给他。就是说,根据B,C,D的物品列表,我们形成了一个商品集合。我们在这个集合列表中找到那些用户A还没有把玩过的东西,推荐给他。
2. 具体过程
一个关键问题就是我们如何计算用户的兴趣相似度?方法有很多,根据书中的描述呢,有jaccard公式,余弦相似度,另外还有欧式距离,曼哈顿距离等等。最终选择什么方法,取决于实际的应用环境。书中实现的是余弦相似度。(N(u)表示用户u曾有过正反馈的物品集合,也就是用户u评论过的那些商品。)
同样用书中的例子说明该算法。A买过{a,b,d},B买过{a,c},那么利用余弦相似度计算的A和B的兴趣相似度为(分子是他们共同买过的东西,分母是分别买的东西的数量):
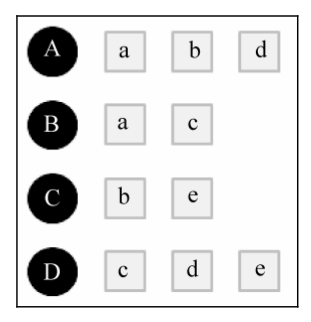
所有用户的具体购物情况如下表:
以此类推,A和B,C,D的相似度计算书中有,不赘述。
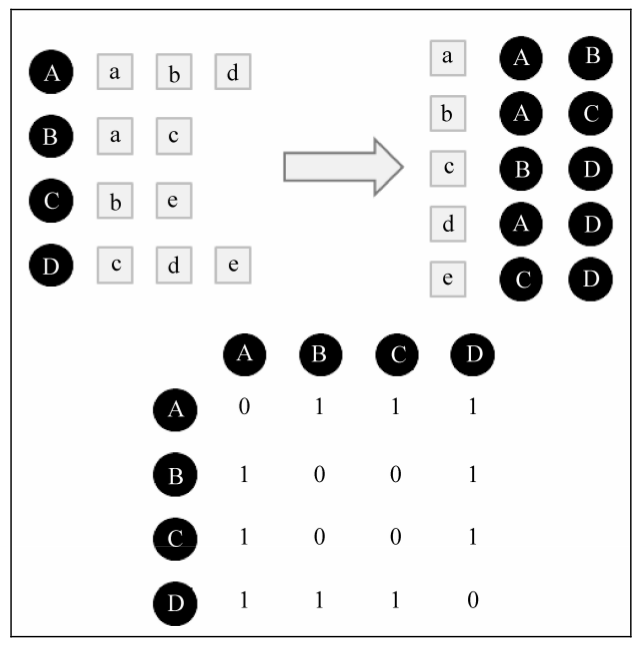
实际情况是很多用户没有买过相同的商品,那么存在时间复杂度过大的问题。为了解决这个问题,引入倒排表的概念。同样使用上面的例子。我们先要建立一个物品-用户的倒排表,接着建立一个4×4的用户相似度矩阵W。矩阵默认是0阵,那么如果两个用户在同一个商品下,那么矩阵中他们对应的值就加一。最终我们会得到一个余弦相似度中分子部分的矩阵。最后我们再除以对应的分母,就可以得到最终用户的兴趣相似度了。如下图,具体过程请看书。
具体实现如下:(整体结构和书中差不多,某些细节上我按自己的理解写的。不当之处,还请指正。)
# -*- coding=utf-8 -*-
import math
#例子中的数据相当于是一个用户字典{A:(a,b,d),B:(a,c),C:(b,e),D:(c,d,e)}
#我们这样存储原始输入数据
dic={'A':('a','b','d'),'B':('a','c'),'C':('b','e'),'D':('c','d','e')}#简单粗暴,记得加''
#计算用户兴趣相似度
def Usersim(dicc):
#把用户-商品字典转成商品-用户字典(如图中箭头指示那样)
item_user=dict()
for u,items in dicc.items():
for i in items:#文中的例子是不带评分的,所以用的是元组而不是嵌套字典。
if i not in item_user.keys():
item_user[i]=set()#i键所对应的值是一个集合(不重复)。
item_user[i].add(u)#向集合中添加用户。
C=dict()#感觉用数组更好一些,真实数据集是数字编号,但这里是字符,这边还用字典。
N=dict()
for item,users in item_user.items():
for u in users:
if u not in N.keys():
N[u]=0 #书中没有这一步,但是字典没有初始值不可以直接相加吧
N[u]+=1 #每个商品下用户出现一次就加一次,就是计算每个用户一共购买的商品个数。
#但是这个值也可以从最开始的用户表中获得。
#比如: for u in dic.keys():
# N[u]=len(dic[u])
for v in users:
if u==v:
continue
if (u,v) not in C.keys():#同上,没有初始值不能+=
C[u,v]=0
C[u,v]+=1 #这里我不清楚书中是不是用的嵌套字典,感觉有点迷糊。所以我这样用的字典。
#到这里倒排阵就建立好了,下面是计算相似度。
W=dict()
for co_user,cuv in C.items():
W[co_user]=cuv / math.sqrt(N[co_user[0]]*N[co_user[1]])
return W
把W输出看看:
计算完兴趣相似度,我们就要用UserCF算法做推荐了。我们给目标用户u推荐K个他可能喜欢的商品。那么目标用户u对物品i的兴趣程度:
(我直接把书中这部分解释复制过来了,也比较详细)
(解释一下就是:在K个兴趣相近的用户中找对物品i感兴趣的几个人,然后用每个人的用户相似度乘以对物品的兴趣度就得到目标用户可能对物品的兴趣度,最后把他们几个人加起来。)
具体的代码实现如下:
def Recommend(user,dicc,W2,K):
rvi=1 #这里都是1,实际中可能每个用户就不一样了。就像每个人都喜欢beautiful girl,但有的喜欢可爱的多一些,有的喜欢御姐多一些。
rank=dict()
related_user=[]
interacted_items=dicc[user]
for co_user,item in W2.items():
if co_user[0]==user:
related_user.append((co_user[1],item))#先建立一个和待推荐用户兴趣相关的所有的用户列表。
for v,wuv in sorted(related_user,key=itemgetter(1),reverse=True)[0:K]:
#找到K个相关用户以及对应兴趣相似度,按兴趣相似度从大到小排列。itemgetter要导包。
for i in dicc[v]:
if i in interacted_items:
continue #书中少了continue这一步吧?
if i not in rank.keys():#如果不写要报错,是不是有更好的方法?
rank[i]=0
rank[i]+=wuv*rvi
return rank
结果如下:
这样我们已经得到了一个待推荐字典了。{商品:待推荐用户对商品的兴趣,......}
我用书中的例子数据将整个过程跑了一遍,能够更好的理解整个过程。如果有朋友要跑真实的MovieLens数据集,我推荐看这个博文(亲测有效):
http://blog.csdn.net/ygrx/article/details/15501679
接下来贴上完整代码:
# -*- coding=utf-8 -*-
import math
from operator import *
#例子中的数据相当于是一个用户字典{A:(a,b,d),B:(a,c),C:(b,e),D:(c,d,e)}
#我们这样存储原始输入数据
dic={'A':('a','b','d'),'B':('a','c'),'C':('b','e'),'D':('c','d','e')}#简单粗暴,记得加''
#计算用户兴趣相似度
def Usersim(dicc):
#把用户-商品字典转成商品-用户字典(如图中箭头指示那样)
item_user=dict()
for u,items in dicc.items():
for i in items:#文中的例子是不带评分的,所以用的是元组而不是嵌套字典。
if i not in item_user.keys():
item_user[i]=set()#i键所对应的值是一个集合(不重复)。
item_user[i].add(u)#向集合中添加用户。
C=dict()#感觉用数组更好一些,真实数据集是数字编号,但这里是字符,这边还用字典。
N=dict()
for item,users in item_user.items():
for u in users:
if u not in N.keys():
N[u]=0 #书中没有这一步,但是字典没有初始值不可以直接相加吧
N[u]+=1 #每个商品下用户出现一次就加一次,就是计算每个用户一共购买的商品个数。
#但是这个值也可以从最开始的用户表中获得。
#比如: for u in dic.keys():
# N[u]=len(dic[u])
for v in users:
if u==v:
continue
if (u,v) not in C.keys():#同上,没有初始值不能+=
C[u,v]=0
C[u,v]+=1 #这里我不清楚书中是不是用的嵌套字典,感觉有点迷糊。所以我这样用的字典。
#到这里倒排阵就建立好了,下面是计算相似度。
W=dict()
for co_user,cuv in C.items():
W[co_user]=cuv / math.sqrt(N[co_user[0]]*N[co_user[1]])#因为我不是用的嵌套字典,所以这里有细微差别。
return W
def Recommend(user,dicc,W2,K):
rvi=1 #这里都是1,实际中可能每个用户就不一样了。就像每个人都喜欢beautiful girl,但有的喜欢可爱的多一些,有的喜欢御姐多一些。
rank=dict()
related_user=[]
interacted_items=dicc[user]
for co_user,item in W2.items():
if co_user[0]==user:
related_user.append((co_user[1],item))#先建立一个和待推荐用户兴趣相关的所有的用户列表。
for v,wuv in sorted(related_user,key=itemgetter(1),reverse=True)[0:K]:
#找到K个相关用户以及对应兴趣相似度,按兴趣相似度从大到小排列。itemgetter要导包。
for i in dicc[v]:
if i in interacted_items:
continue #书中少了continue这一步吧?
if i not in rank.keys():#如果不写要报错,是不是有更好的方法?
rank[i]=0
rank[i]+=wuv*rvi
return rank
if __name__=='__main__':
W3=Usersim(dic)
Last_Rank=Recommend('A',dic,W3,2)
print Last_Rank
因本人代码能力有限,实为初学,为加深理解故走了一遍流程。不当之处,还望大家指正。











 本文详细介绍基于用户的协同过滤推荐算法实现过程,包括用户兴趣相似度计算及推荐算法的具体步骤,并提供Python代码示例。
本文详细介绍基于用户的协同过滤推荐算法实现过程,包括用户兴趣相似度计算及推荐算法的具体步骤,并提供Python代码示例。
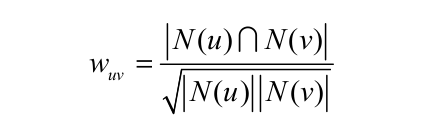
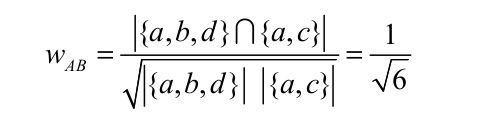




















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










