匈牙利算法python代码实现以及原理图解

1、匈牙利算法python代码实现：

scipy中有对应的接口scipy.optimize.linear_sum_assignment，输入代价矩阵，即可得到分配问题的结果：

    >>> cost = np.array([[4, 1, 3], [2, 0, 5], [3, 2, 2]])
    >>> from scipy.optimize import linear_sum_assignment
    >>> row_ind, col_ind = linear_sum_assignment(cost)
    >>> col_ind
    array([1, 0, 2])
    >>> cost[row_ind, col_ind].sum()
    5

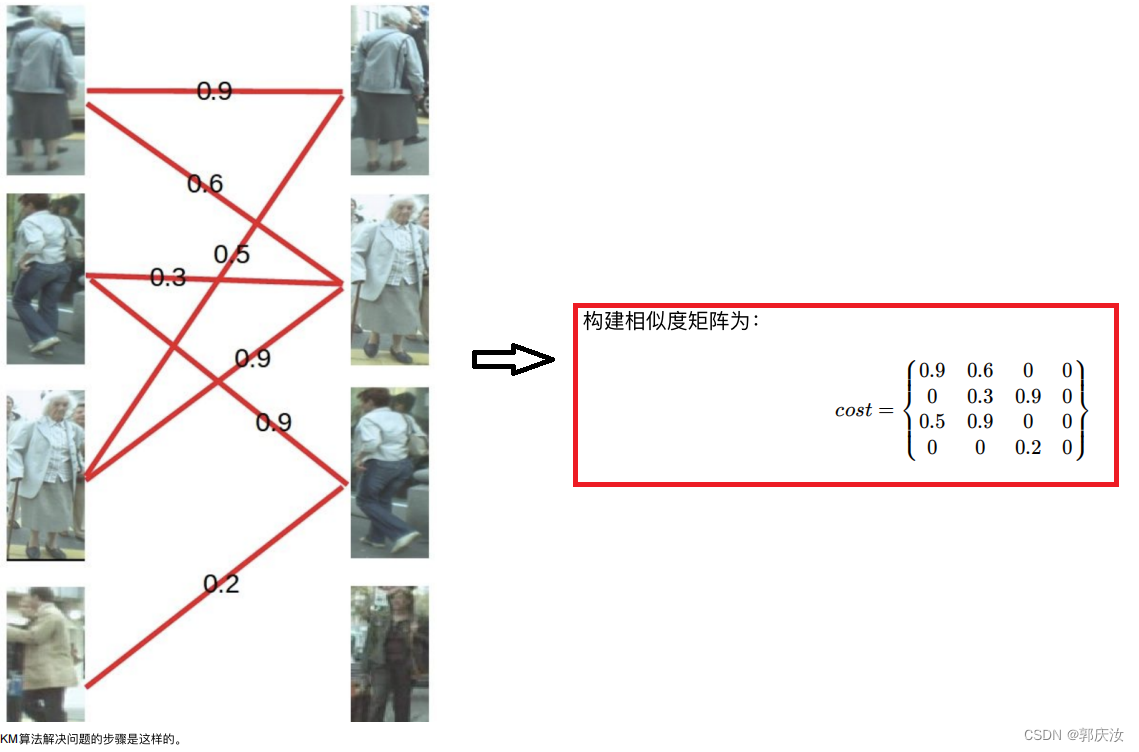
代码示例：

from scipy.optimize import linear_sum_assignment
import numpy as np
# 代价矩阵
cost =np.array([[0.9,0.6,0,0],[0,0.3,0.9,0],[0.5,0.9,0,0],[0,0,0.2,0]])
# 匹配结果：该⽅法的⽬的是代价最⼩，这⾥是求最⼤匹配，所以将cost取负数
row_ind,col_ind=linear_sum_assignment(-cost)
#对应的⾏索引
print("⾏索引：\n{}".format(row_ind))
#对应⾏索引的最优指派的列索引
print("列索引：\n{}".format(col_ind))
#提取每个⾏索引的最优指派列索引所在的元素，形成数组
print("匹配度：\n{}".format(cost[row_ind,col_ind]))

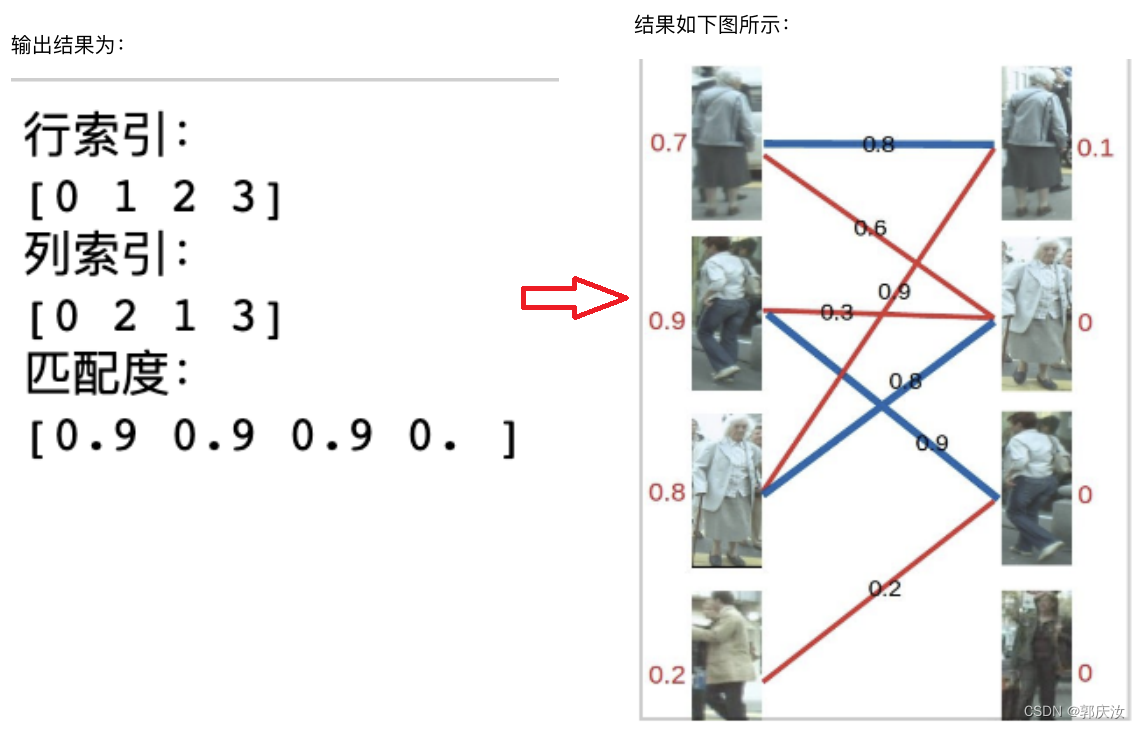
scipy.optimize.linear_sum_assignment的源码如下：

# Hungarian algorithm (Kuhn-Munkres) for solving the linear sum assignment
# problem. Taken from scikit-learn. Based on original code by Brian Clapper,
# adapted to NumPy by Gael Varoquaux.
# Further improvements by Ben Root, Vlad Niculae and Lars Buitinck.
#
# Copyright (c) 2008 Brian M. Clapper <bmc@clapper.org>, Gael Varoquaux
# Author: Brian M. Clapper, Gael Varoquaux
# License: 3-clause BSD

import numpy as np


def linear_sum_assignment(cost_matrix):
    """Solve the linear sum assignment problem.
    The linear sum assignment problem is also known as minimum weight matching
    in bipartite graphs. A problem instance is described by a matrix C, where
    each C[i,j] is the cost of matching vertex i of the first partite set
    (a "worker") and vertex j of the second set (a "job"). The goal is to find
    a complete assignment of workers to jobs of minimal cost.
    Formally, let X be a boolean matrix where :math:`X[i,j] = 1` iff row i is
    assigned to column j. Then the optimal assignment has cost
    .. math::
        \min \sum_i \sum_j C_{i,j} X_{i,j}
    s.t. each row is assignment to at most one column, and each column to at
    most one row.
    This function can also solve a generalization of the classic assignment
    problem where the cost matrix is rectangular. If it has more rows than
    columns, then not every row needs to be assigned to a column, and vice
    versa.
    The method used is the Hungarian algorithm, also known as the Munkres or
    Kuhn-Munkres algorithm.
    Parameters
    ----------
    cost_matrix : array
        The cost matrix of the bipartite graph.
    Returns
    -------
    row_ind, col_ind : array
        An array of row indices and one of corresponding column indices giving
        the optimal assignment. The cost of the assignment can be computed
        as ``cost_matrix[row_ind, col_ind].sum()``. The row indices will be
        sorted; in the case of a square cost matrix they will be equal to
        ``numpy.arange(cost_matrix.shape[0])``.
    Notes
    -----
    .. versionadded:: 0.17.0
    Examples
    --------
    >>> cost = np.array([[4, 1, 3], [2, 0, 5], [3, 2, 2]])
    >>> from scipy.optimize import linear_sum_assignment
    >>> row_ind, col_ind = linear_sum_assignment(cost)
    >>> col_ind
    array([1, 0, 2])
    >>> cost[row_ind, col_ind].sum()
    5
    References
    ----------
    1. http://csclab.murraystate.edu/bob.pilgrim/445/munkres.html
    2. Harold W. Kuhn. The Hungarian Method for the assignment problem.
       *Naval Research Logistics Quarterly*, 2:83-97, 1955.
    3. Harold W. Kuhn. Variants of the Hungarian method for assignment
       problems. *Naval Research Logistics Quarterly*, 3: 253-258, 1956.
    4. Munkres, J. Algorithms for the Assignment and Transportation Problems.
       *J. SIAM*, 5(1):32-38, March, 1957.
    5. https://en.wikipedia.org/wiki/Hungarian_algorithm
    """
    cost_matrix = np.asarray(cost_matrix)
    if len(cost_matrix.shape) != 2:
        raise ValueError("expected a matrix (2-d array), got a %r array"
                         % (cost_matrix.shape,))

    # The algorithm expects more columns than rows in the cost matrix.
    '''代价矩阵需要列数 ≥ 行数'''
    if cost_matrix.shape[1] < cost_matrix.shape[0]:
        cost_matrix = cost_matrix.T
        transposed = True
    else:
        transposed = False

    state = _Hungary(cost_matrix)

    # No need to bother with assignments if one of the dimensions
    # of the cost matrix is zero-length.
    step = None if 0 in cost_matrix.shape else _step1

    while step is not None:
        step = step(state)

    if transposed:
        marked = state.marked.T
    else:
        marked = state.marked
    return np.where(marked == 1)


class _Hungary(object):
    """State of the Hungarian algorithm.
    Parameters
    ----------
    cost_matrix : 2D matrix
        The cost matrix. Must have shape[1] >= shape[0].
    """

    def __init__(self, cost_matrix):
        self.C = cost_matrix.copy()

        n, m = self.C.shape
        self.row_uncovered = np.ones(n, dtype=bool)
        self.col_uncovered = np.ones(m, dtype=bool)
        self.Z0_r = 0
        self.Z0_c = 0
        self.path = np.zeros((n + m, 2), dtype=int)
        self.marked = np.zeros((n, m), dtype=int)

    def _clear_covers(self):
        """Clear all covered matrix cells"""
        self.row_uncovered[:] = True
        self.col_uncovered[:] = True


# Individual steps of the algorithm follow, as a state machine: they return
# the next step to be taken (function to be called), if any.

def _step1(state):
    """Steps 1 and 2 in the Wikipedia page."""

    """
    Step 1: For each row of the matrix, find the smallest element and
    subtract it from every element in its row.    
    减去每一行的最小值
    """
    state.C -= state.C.min(axis=1)[:, np.newaxis]
    
    """
    Step 2: Find a zero (Z) in the resulting matrix. If there is no
    starred zero in its row or column, star Z. Repeat for each element
    in the matrix.    
    如果一行或列中没有星标的0，则标记0*
    """
    for i, j in zip(*np.where(state.C == 0)):
        if state.col_uncovered[j] and state.row_uncovered[i]:
            state.marked[i, j] = 1
            state.col_uncovered[j] = False
            state.row_uncovered[i] = False

    state._clear_covers()
    return _step3


def _step3(state):
    """
    Step3：Cover each column containing a starred zero. If n columns are covered,
    the starred zeros describe a complete set of unique assignments.
    In this case, Go to DONE, otherwise, Go to Step 4.
    
    覆盖每列包含加星号的零。如果覆盖了n列，加星号的零表示完整的唯一结果集。
    """
    marked = (state.marked == 1)
    state.col_uncovered[np.any(marked, axis=0)] = False

    if marked.sum() < state.C.shape[0]:
        return _step4


def _step4(state):
    """
    Step4：Find a noncovered zero and prime it. If there is no starred zero
    in the row containing this primed zero, Go to Step 5. Otherwise,
    cover this row and uncover the column containing the starred
    zero. Continue in this manner until there are no uncovered zeros
    left. Save the smallest uncovered value and Go to Step 6.
    
    找到一个未覆盖的零并将其准备好。 如果准备好的零所在行中没有加星号的零，
    请转到步骤5。否则，覆盖该行并找出包含加注星号的零的列。 继续以这种方式
    进行操作，直到没有剩余的零为止。保存最小的发现值，然后转到步骤6。
    """
    # We convert to int as numpy operations are faster on int
    C = (state.C == 0).astype(int)
    covered_C = C * state.row_uncovered[:, np.newaxis]
    covered_C *= np.asarray(state.col_uncovered, dtype=int)
    n = state.C.shape[0]
    m = state.C.shape[1]

    while True:
        # Find an uncovered zero
        row, col = np.unravel_index(np.argmax(covered_C), (n, m))
        if covered_C[row, col] == 0:
            return _step6
        else:
            state.marked[row, col] = 2
            # Find the first starred element in the row
            star_col = np.argmax(state.marked[row] == 1)
            if state.marked[row, star_col] != 1:
                # Could not find one
                state.Z0_r = row
                state.Z0_c = col
                return _step5
            else:
                col = star_col
                state.row_uncovered[row] = False
                state.col_uncovered[col] = True
                covered_C[:, col] = C[:, col] * (
                    np.asarray(state.row_uncovered, dtype=int))
                covered_C[row] = 0


def _step5(state):
    """
    Step5：Construct a series of alternating primed and starred zeros as follows.
    Let Z0 represent the uncovered primed zero found in Step 4.
    Let Z1 denote the starred zero in the column of Z0 (if any).
    Let Z2 denote the primed zero in the row of Z1 (there will always be one).
    Continue until the series terminates at a primed zero that has no starred
    zero in its column. Unstar each starred zero of the series, star each
    primed zero of the series, erase all primes and uncover every line in the
    matrix. Return to Step 3

	构造如下一系列交替的填色和加星号的零：
     令Z0代表在步骤4中发现的未覆盖的准备好的零 0'。
     令Z1表示Z0列中的星号零 0*（如果有的话）。
     令Z2表示Z1行中的准备好的零 0'（始终为1个）。
     继续直到0'所在列没有星标0*，终止该序列。取消对每个已加星标的零的星标，对系列中的每个0'加星标，去除所有的'和覆盖线。 返回步骤3。
    """
    count = 0
    path = state.path
    path[count, 0] = state.Z0_r
    path[count, 1] = state.Z0_c

    while True:
        # Find the first starred element in the col defined by
        # the path.
        row = np.argmax(state.marked[:, path[count, 1]] == 1)
        if state.marked[row, path[count, 1]] != 1:
            # Could not find one
            break
        else:
            count += 1
            path[count, 0] = row
            path[count, 1] = path[count - 1, 1]

        # Find the first prime element in the row defined by the
        # first path step
        col = np.argmax(state.marked[path[count, 0]] == 2)
        if state.marked[row, col] != 2:
            col = -1
        count += 1
        path[count, 0] = path[count - 1, 0]
        path[count, 1] = col

    # Convert paths
    for i in range(count + 1):
        if state.marked[path[i, 0], path[i, 1]] == 1:
            state.marked[path[i, 0], path[i, 1]] = 0
        else:
            state.marked[path[i, 0], path[i, 1]] = 1

    state._clear_covers()
    # Erase all prime markings
    state.marked[state.marked == 2] = 0
    return _step3


def _step6(state):
    """
    Step 6: Add the value found in Step 4 to every element of each covered row,
    and subtract it from every element of each uncovered column.
    Return to Step 4 without altering any stars, primes, or covered lines.
	
	将在第4步中找到的值添加到每个覆盖行的每个元素中，
    并将其从每个未覆盖列的每个元素中减去。
    返回第4步，而不更改任何星号，或遮盖线。
    """
    # the smallest uncovered value in the matrix
    if np.any(state.row_uncovered) and np.any(state.col_uncovered):
        minval = np.min(state.C[state.row_uncovered], axis=0)
        minval = np.min(minval[state.col_uncovered])
        state.C[~state.row_uncovered] += minval
        state.C[:, state.col_uncovered] -= minval
    return _step4

2、原理图解：

算法原理B站视频讲解