【算法】网络流基本概念

前言：本文为网络流的基本概念，不涉及到任何算法的代码实现。

---

一. 流网络

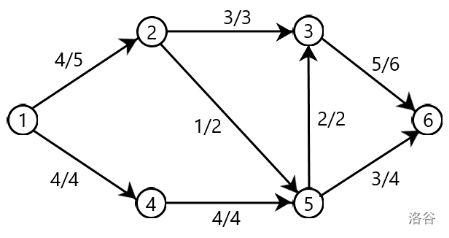
网络流仅限于有向图，所构成的图即名为流网络，将其记为 $G=(V,E)$ （$V$ 是点集，$E$ 是边集），不考虑反向边。

流网络是一个有向图（与环无关），其中有两个特殊的点，分别为源点 $s$ 和汇点 $t$，如上图 $1$ 即为源点，$6$ 即为汇点。

在流网络中，每条边都有两个特殊的量，流量 $f$ 和容量 $c$。我们可以将每条边想象成一个水管，其中，容量即为这条水管最大流水量，流量即为这个水管实际流的水量。源点有无穷多的流量，最终都将汇入汇点。

对于任意的流网络，都会有一种方案，可以从源点流向汇点。这个方案即为可行流。可行流可能不是只流一条路径，而是很多条路径同时流。

对于任意的可行流（不考虑反向边），我们都要满足以下两个条件。

• 对于每一条属于流网络的边，它的流量一定小于等于容量且必须大于等于 $0$，即

$$0\le f(u,v)\le c(u,v)$$

• 对于每一条属于流网络的边，它的流量一定是守恒的，就代表所流进的流量永远等于所流出的流量（源点汇点除外），即

∀ x ∈ { V ∣ ¬ S , ¬ T } , ∑ ( u , x ) ∈ E f ( u , x ) = ∑ ( x , v ) ∈ E f ( x , v ) \displaystyle\forall x\in \{V|\neg S, \neg T\},\sum_{(u,x)\in E} f(u,x)=\sum_{(x,v)\in E} f(x,v) ∀x∈{V∣¬S,¬T},(u,x)∈E∑​f(u,x)=(x,v)∈E∑​f(x,v)

只要满足上述条件，流 $f$ 即为可行流。$|f|$ 表示每条可行流的流量，也就是流出源点的从流量与流入源点的总流量之差，即

$$|f|=\sum _{(s,v)\in E}f(s,v)-\sum _{(v,s)\in E}f(v,s)$$

最大流为最大可行流。

---

二. 残留网络

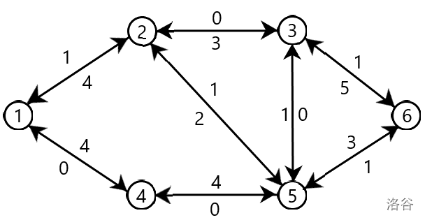
对于每一条可行流，皆有一个残留网络，记为 $G_f$。其中，$V_f=V,E_f=E$

以图 $1$ 为例，它的残留网络即为上图。

它是由一个和流网络中一样方向的边和反向边组成的，容量分别为流网络中剩余的流量和流网络中流过的流量，即

$$\{\begin{array}{l}{c}^{\prime }(u,v)=c(u,v)-f(u,v)((u,v)\in E)\\ c^{\prime }(v,u)=f(u,v)((v,u)\in E)\end{array}$$

再之后求网络流的问题时，反向边可以提供给我们一个反悔的机会，使算法更优。

在残留网络中，有一个定理，任意一个在残留网络中的可行流和再流网络中的可行流之和，在流网络中一定也是一个流网络（这里的相加指的是对应边相加，反向边相减，所以对应边不同无法相加）。

这里简单证一下：

如果任意一个在残留网络中的可行流和再流网络中的可行流之和也是一个可行流的话，那么它必须满足两个可行流的限制。

我们从通向边和反向边分别证一下。

同向边（容量限制）：

$$f^{\prime }(u,v)\le c^{\prime }(u,v)=c(u,v)-f(u,v)$$

$$f^{\prime }(u,v)+f(u,v)\le c(u,v)$$

反向边（容量限制）：

$$f^{\prime }(v,u)\le c^{\prime }(v,u)=f(u,v)\le c(u,v)$$

$$f(u,v)-f^{\prime }(v,u)\le c(u,v)$$

同向边（流量守恒）：

∀ x ∈ { V ∣ ¬ S , ¬ T } , ∑ ( u , x ) ∈ E f ( u , x ) = ∑ ( x , v ) ∈ E f ( x , v ) \displaystyle\forall x\in \{V|\neg S, \neg T\},\sum_{(u,x)\in E} f(u,x)=\sum_{(x,v)\in E} f(x,v) ∀x∈{V∣¬S,¬T},(u,x)∈E∑​f(u,x)=(x,v)∈E∑​f(x,v)

∀ x ∈ { V ′ ∣ ¬ S ′ , ¬ T ′ } , ∑ ( u , x ) ∈ E ′ f ′ ( u , x ) = ∑ ( x , v ) ∈ E ′ f ′ ( x , v ) \displaystyle\forall x\in \{V'|\neg S', \neg T'\},\sum_{(u,x)\in E'} f'(u,x)=\sum_{(x,v)\in E'} f'(x,v) ∀x∈{V′∣¬S′,¬T′},(u,x)∈E′∑​f′(u,x)=(x,v)∈E′∑​f′(x,v)

$$\sum _{(u,x)\in E}f(u,x)+\sum _{(u,x)\in E^{\prime }}{f}^{\prime }(u,x)=\sum _{(x,v)\in E}f(x,v)+\sum _{(x,v)\in E^{\prime }}{f}^{\prime }(x,v)$$

反向边（流量守恒）：

∀ x ∈ { V ∣ ¬ S , ¬ T } , ∑ ( u , x ) ∈ E f ( u , x ) = ∑ ( x , v ) ∈ E f ( x , v ) \displaystyle\forall x\in \{V|\neg S, \neg T\},\sum_{(u,x)\in E} f(u,x)=\sum_{(x,v)\in E} f(x,v) ∀x∈{V∣¬S,¬T},(u,x)∈E∑​f(u,x)=(x,v)∈E∑​f(x,v)

∀ x ∈ { V ′ ∣ ¬ S ′ , ¬ T ′ } , ∑ ( x , u ) ∈ E ′ f ′ ( x , u ) = ∑ ( v , x ) ∈ E ′ f ′ ( v , x ) \displaystyle\forall x\in \{V'|\neg S', \neg T'\},\sum_{(x,u)\in E'} f'(x,u)=\sum_{(v,x)\in E'} f'(v,x) ∀x∈{V′∣¬S′,¬T′},(x,u)∈E′∑​f′(x,u)=(v,x)∈E′∑​f′(v,x)

$$\sum _{(u,x)\in E}f(u,x)-\sum _{(x,u)\in E^{\prime }}{f}^{\prime }(x,u)=\sum _{(x,v)\in E}f(x,v)-\sum _{(v,x)\in E^{\prime }}{f}^{\prime }(v,x)$$

证毕。

---

三. 增广路

增广路是在一个残留网络之中，从源点沿着容量非 $0$ 的边走到汇点的一条路径。如图 $2$，此图中的增广路即为 $1\to 2\to 5\to 6$ （增广路有可能不止一条）。

增广路定理：如果在残留网络 $G_f$ 中没有增广路，那么最大流即为 $f$。

证明：因为如果有一条增广路，也就代表有一条可行流 $f^{\prime }$，那么此时最大流就应该为上一个定理的结论 $f+f^{\prime }$。

---

四. 割

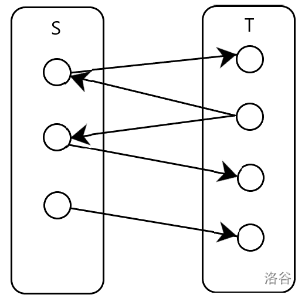
割是在一个流网络中，将它分成两个子图后的流网络。

两个子集为 $S$ 和 $T$，分别包含源点和终点。其中 $S\cup T=V$，$S\cap T=\emptyset $

割的容量为所有从点集 $S$ 中的点连向点集 $T$ 中的点的所有边的容量，不考虑反向边，即

$$c(S,T)=\sum _{u\in S}\sum _{v\in T}c(u,v)$$

最小割是指容量最小的割。

割的流量为所有从点集 $S$ 中的点流向点集 $T$ 中的点的边的流量减去所有从子图 $T$ 流向子图 $S$ 的流量，即

$$f(S,T)=\sum _{u\in S}\sum _{v\in T}f(u,v)-\sum _{u\in S}\sum _{v\in T}f(v,u)$$

在一个割中，只要确定了流网络，就确定了割的容量，但不能确定割的流量。

注：因为割也是一个流网络，所以它继承了所有流网络的性质。

在我们了解完割的定义后，我们来了解一个定理

对于任意一个割的流量一定等于任意一个原流网络中一个可行流的流量，即

$$f(S,T)=|f|$$

在证明这个定理之前，我们还需要四个引理：

对于任意的点集 $X$，$Y$，$Z$ 且 $X\cap Y=\varnothing$ 都有

1. $f(X,Y)=-f(Y,X)$ 这个比较显然，就不做证明。

2. $f(X,X)$ 因为在一个点集当中，流出与流进的流量差为 $0$。

3. $f(Z,X\cup Y)=f(Z,X)+f(Z,Y)$ 因为 $X$ 和 $Y$ 不相交，所以 $(X,Z)$ 和 $(Y,Z)$ 之间没有重复流量，直接相加即可。

4. $f(X\cup Y,Z)=f(X,Z)+f(Y,Z)$ 与上条引理相同

有上述四条引理即可证明，证明过程如下

因为 $S\cup T=V$ 与引理 $3$，所以

$$f(S,S)+f(S,T)=f(S,V)$$

$$f(S,T)=f(S,V)-f(S,S)$$

根据引理 $2$，得

$$f(S,T)=f(S,V)$$

根据引理 $3$，得

f ( S , T ) = f ( s , V ) + f ( { S ∣ ¬ s } , V ) f(S,T)=f(s,V)+f(\{S|\neg s\},V) f(S,T)=f(s,V)+f({S∣¬s},V)

设 S ′ = { S ∣ ¬ s } S'=\{S|\neg s\} S′={S∣¬s}。因为第二项的点集 $S$ 除去了源点，所以它的流量即为

$$f(S^{\prime },V)=\sum _{u\in S^{\prime }}\sum _{v\in V}f(u,v)-\sum _{u\in S^{\prime }}\sum _{v\in V}f(v,u)$$

$$f(S^{\prime },V)=\sum _{u\in S^{\prime }}(\sum _{v\in V}f(u,v)-\sum _{v\in V}f(v,u))$$

因为在点集 $V$ 所属的流网络中，流量守恒，所以 $f(S^{\prime },V)=0$，即

$$f(S,T)=f(s,V)=|f|$$

证毕。

根据这个定理，我们还可以证出以下结论

$$\forall |f|\in G,|f|=f(S,T)\le c(S,T)$$

所以当 $|f|$ 取最大流时小于等于最小割。

---

五. 最大流最小割定理

1. $f$ 是最大流
2. $G_f$ 中不存在增广路
3. $\exists [S,T],|f|=c(S,T)$

最大流最小割定理是由上述三个推论假设其中一个再由假设的推论推出的，证明过程如下

• $1\iff 2$

  由增广路定理可得。

• $1\iff 3$

  证明这个推论可以用两个方面来证明。

  首先，由上述定理可得 $|f|$ 取最大流时小于等于最小割。

  因为 $|f|=c(S,T)$，所以最小割 $\le c(S,T)=|f|\le$ 最大流。

  因为最大流小于等于最小割，最小割小于等于最大流，所以最小割等于最大流。

  此时，$f$ 为最大流。

• $2\iff 3$

  由增广路定理推第一条再推一下第三条即可。