逻辑回归(logistics regression)
一、逻辑回归的概念
逻辑回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。逻辑回归从本质来说属于二分类问题。
二分类问题是指预测的结果只有两种独立的情况,即
y
y
y值只能取0或者1代表不同的结果,例如,一个人要么是左撇子,要么是右撇子,那么用0来表示左撇子,1来表示右撇子,我们就可以构造一个映射
X
→
Y
X \to Y
X→Y,其中
X
=
{
所有人
}
X = \{ \text{所有人} \}
X={所有人},
Y
=
{
0
,
1
}
Y = \{ 0, 1 \}
Y={0,1},这就是一个二分类问题。
1. 回顾线性回归
我们之前学过的线性回归模型是对于给定的特征 x \bm{x} x,给定目标值 y \bm{y} y,构造待求解的目标函数 h θ ( x ) = θ T x h_\theta(\bm{x}) = \bm{\theta}^T\bm{x} hθ(x)=θTx,其中 θ = ( θ 0 θ 1 ⋯ θ n ) T \bm{\theta} = \begin{pmatrix} \theta_0 & \theta_1 & \cdots & \theta_n \end{pmatrix}^T θ=(θ0θ1⋯θn)T, x = ( 1 x 1 ⋯ x n ) T \bm{x} = \begin{pmatrix}1 & x_1 & \cdots & x_n \end{pmatrix}^T x=(1x1⋯xn)T,通过各种方式(例如梯度下降法、共轭梯度法、牛顿法、 ⋯ \cdots ⋯)使误差函数 J ( θ ) = 1 2 ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\bm{\theta}) = \cfrac{1}{2} \displaystyle\sum_{i = 1}^{n} \left(h_\theta(\bm{x}^{(i)}) - y^{(i)}\right)^2 J(θ)=21i=1∑n(hθ(x(i))−y(i))2取到最小值,从而使目标函数 h θ ( x ) h_\theta(\bm{x}) hθ(x)能够很好地刻画目标值 y \boldsymbol{y} y,从而得到线性回归模型 h θ ( x ) h_\theta(\bm{x}) hθ(x).
2. 为什么要用逻辑回归
那么既然已经有线性回归了,为什么我们还要研究逻辑回归?
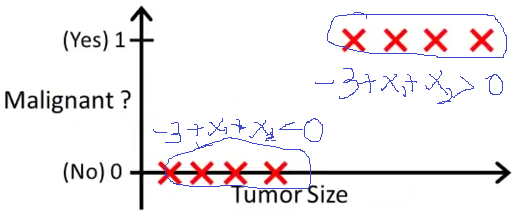
我们来看这样一个例子:下图是肿瘤的大小与肿瘤是否是恶性的之间的关系。其中我们用 0 0 0去表示良性肿瘤,用 1 1 1去表示恶性肿瘤。
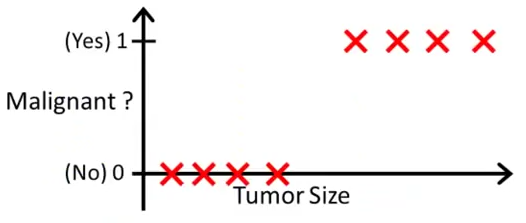
那么这时候我们如果用线性回归去建模,就会得到如下图所示的一条直线,其中当 h θ ( t u m o r S i z e ) > 0.5 h_\theta(\mathrm{tumorSize}) \gt 0.5 hθ(tumorSize)>0.5时,我们预测 m a l i g n a n t = 1 \mathrm{malignant} = 1 malignant=1;当 h θ ( t u m o r S i z e ) < 0.5 h_\theta(\mathrm{tumorSize}) \lt 0.5 hθ(tumorSize)<0.5时,我们预测 m a l i g n a n t = 0 \mathrm{malignant} = 0 malignant=0。
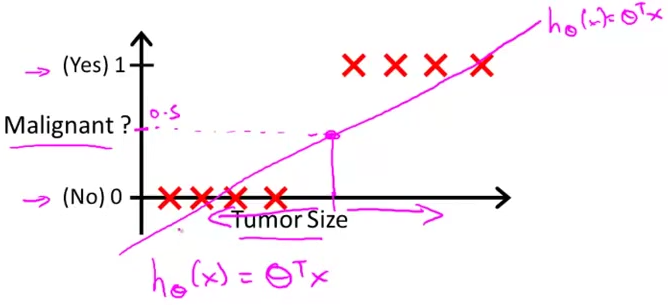
但是如果我们得到的训练集是如下图所示的,那么就会训练出来一条斜率略小的直线。
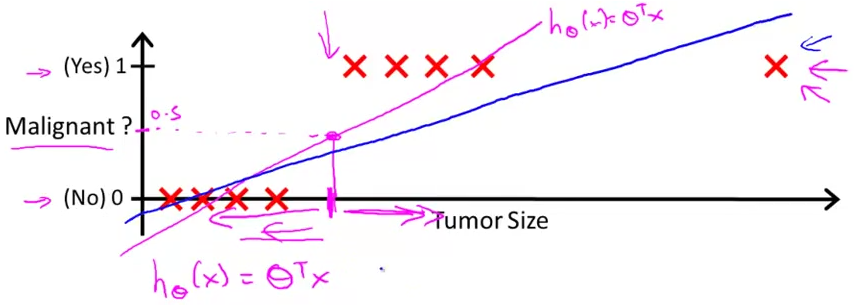
这时我们画出 m a l i g n a n t = 0.5 \mathrm{malignant} = 0.5 malignant=0.5这条直线,从下图中我们可以有相当一部分恶性肿瘤如果按照肿瘤大小去划分,则被分为了良性肿瘤,导致了划分的不准确。
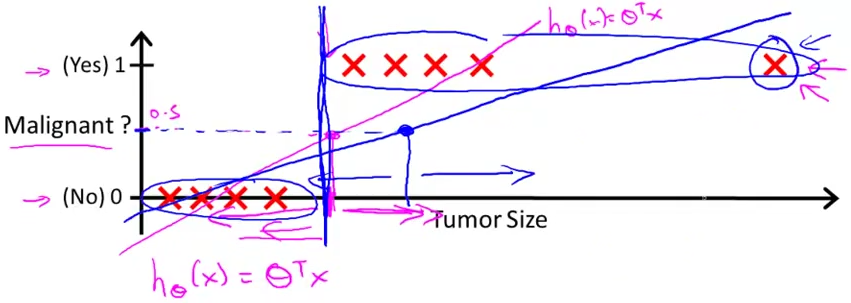
所以为了划分集的准确性,我们引入了逻辑回归。
二、逻辑回归
那么对于上面那个问题,线性回归会导致分类效果很差,所以我们需要一个可以很好拟合上面训练集的模型。
考虑Sigmoid函数 g ( z ) = 1 1 + e − z g(z)=\cfrac{1}{1+e^{-z}} g(z)=1+e−z1,其函数图形如下图所示。
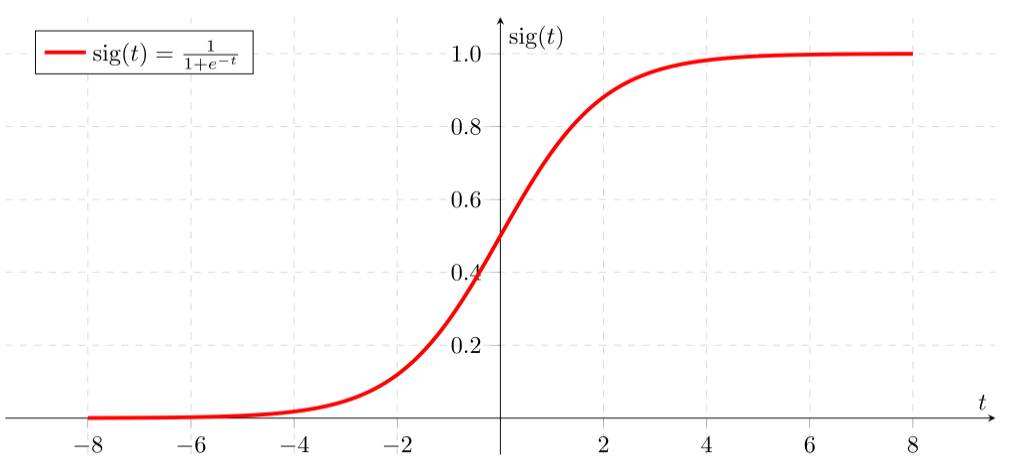
我们发现在做二分类问题时,Sigmoid函数开始趋于平缓,然后急速上升,最后又趋于平缓,即Sigmoid处在趋近于0和趋近于1的时候比较多,能将 y = 0 y=0 y=0与 y = 1 y=1 y=1较为准确地划分。
例如,还是用按照肿瘤大小去判断是否为恶性肿瘤这个例子,如果我们用Sigmoid函数去拟合,就会得到如下图所示的结果。
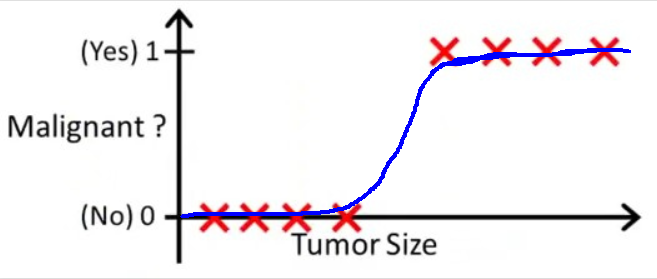
这时如果我们再规定当 h θ ( t u m o r S i z e ) > 0.5 h_\theta(\mathrm{tumorSize}) \gt 0.5 hθ(tumorSize)>0.5时,我们预测 m a l i g n a n t = 1 \mathrm{malignant} = 1 malignant=1;当 h θ ( t u m o r S i z e ) < 0.5 h_\theta(\mathrm{tumorSize}) \lt 0.5 hθ(tumorSize)<0.5时,我们预测 m a l i g n a n t = 0 \mathrm{malignant} = 0 malignant=0,就会得到分类效果更好的模型。
我们把这种用Sigmoid函数去预测二分类问题的模型叫做逻辑回归模型。
1. “回归”的基本原理
-
找一个合适的预测函数(hypothesis),一般表示为 h h h函数,该函数就是我们需要找的分类函数,它用来预测输入数据的判断结果。这个过程时非常关键的,需要对数据有一定的了解或分析,知道或者猜测预测函数的“大概”形式,比如是线性函数还是非线性函数。
-
构造一个 C o s t Cost Cost函数(损失函数),该函数表示预测的输出 h ( x ) h(\boldsymbol{x}) h(x)与训练数据类别 y \boldsymbol{y} y之间的偏差,可以是二者之间的方差 ( h ( x ) − y ) 2 (h(\boldsymbol{x}) - \boldsymbol{y})^2 (h(x)−y)2或者是其他的形式。综合考虑所有训练数据的“损失”,将 C o s t Cost Cost求和或者求平均,记为 J ( θ ) J(\boldsymbol{\theta}) J(θ)函数,表示所有训练数据预测值与实际类别的偏差。
-
显然, J ( θ ) J(\boldsymbol{\theta}) J(θ)函数的值越小表示预测函数越准确(即 h ( x ) h(\boldsymbol{x}) h(x)对 y \boldsymbol{y} y的预测越准确),所以这一步需要做的是找到 J ( θ ) J(\boldsymbol{\theta}) J(θ)函数的最小值。找函数的最小值有很多不同的方法,其中逻辑回归实现时梯度下降法、共轭梯度法和牛顿法居多。
2. 具体过程
(1)引言
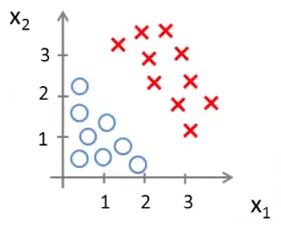
下面我们来考察如下图这样的一个分类问题。现在我想将红色的叉与蓝色的圆圈划分开。
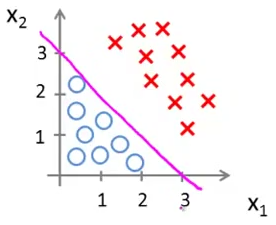
这时我们很容易就能想到用下图中的一条直线就可以将红色的叉与蓝色的圆圈划分开。
但是现在的问题是,我们如何找到这条直线呢?可能有多条直线都能将这两种点分开,哪条直线在面对接下来有可能还要加进来的数据的效果会更好呢?
于是就引入了逻辑回归算法。
(2)逻辑回归模型的构建
现在我们结合之前讲过的预测肿瘤为良性还是恶性的例子,我们发现之所以肿瘤那个例子那么好预测的原因是我们只需要根据0和1来判断肿瘤是良性的还是恶性的,所以现在面对这个划分点的问题,我们是不是也可以像肿瘤那样处理呢?
现在我们令红色的叉就是 y = 1 y=1 y=1,蓝色的圆圈就是 y = 0 y=0 y=0,如下图所示,进行划分。
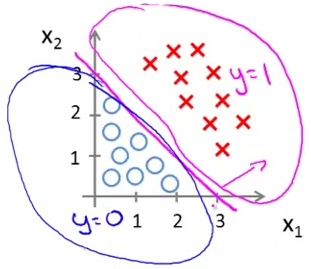
那么对应过去的横坐标又应该是什么呢?我们想一下肿瘤那个例子的横坐标,是肿瘤的大小,换言之,是肿瘤的特征,那么在这个划分叉和圆圈的问题中,叉和圆圈的特征是什么呢?我想答案显而易见,就是这些叉和圆圈所在整个坐标轴中的位置。
所以我们现在想,如何刻画这些圆圈和叉的位置?答案应该是通过叉和圆圈的横纵坐标 x 1 x_1 x1和 x 2 x_2 x2,在这个问题里我们可以清楚地看到当 − 3 + x 1 + x 2 > 0 -3+x_1+x_2 \gt 0 −3+x1+x2>0时坐标平面里分布的全是红色的叉;当 − 3 + x 1 + x 2 < 0 -3+x_1+x_2 \lt 0 −3+x1+x2<0时坐标平面里分布的全是蓝色的圆圈。所以我们以 − 3 + x 1 + x 2 = 0 -3+x_1+x_2 = 0 −3+x1+x2=0为分界线, − 3 + x 1 + x 2 -3+x_1+x_2 −3+x1+x2越小,分布就越是蓝色的圆圈, y y y值就越趋近于 0 0 0, − 3 + x 1 + x 2 -3+x_1+x_2 −3+x1+x2越大,分布就越是蓝色的圆圈, y y y值就越趋近于 1 1 1,这样我们就可以得到一个如下图一样的映射。
于是我们就可以使用Sigmoid函数进行二分类问题的划分。
(3)构造预测函数
对于标准Sigmoid函数 g ( z ) = 1 1 + e − z g(z)=\cfrac{1}{1+e^{-z}} g(z)=1+e−z1,我们可以看到是以 z = 0 z=0 z=0为分界线的,所以我们现在令
h θ ( x ) = g ( θ T x ) = 1 1 + e θ T x h_\theta(\boldsymbol{x}) = g(\boldsymbol{\theta}^T\boldsymbol{x}) = \cfrac{1}{1+e^{{\boldsymbol{\theta}}^T\boldsymbol{x}}} hθ(x)=g(θTx)=1+eθTx1
其中
θ = ( θ 0 θ 1 ⋯ θ n ) T , x = ( 1 x 1 ⋯ x n ) T \bm{\theta} = \begin{pmatrix} \theta_0 & \theta_1 & \cdots & \theta_n \end{pmatrix}^T, \ \bm{x} = \begin{pmatrix} 1 & x_1 & \cdots & x_n \end{pmatrix}^T θ=(θ0θ1⋯θn)T, x=(1x1⋯xn)T
我们不妨设 x 0 = 1 x_0 = 1 x0=1,则
θ T x = ∑ i = 0 n θ i x i = θ 0 + θ 1 x 1 + ⋯ + θ n x n \boldsymbol{\theta}^T\boldsymbol{x} = \sum_{i = 0}^{n} \theta_ix_i = \theta_0 + \theta_1x_1 + \cdots + \theta_nx_n θTx=i=0∑nθixi=θ0+θ1x1+⋯+θnxn
这样的话,我们就成功实现了以 θ T x = 0 \boldsymbol{\theta}^T\boldsymbol{x} = 0 θTx=0为分界的模型,其概率表达为
P ( y = 1 ∣ x ; θ ) = h θ ( x ) P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) \begin{aligned} P(y = 1 \mid \bm{x}; \bm{\theta}) & = h_\theta(\bm{x}) \\ P(y = 0 \mid \bm{x}; \bm{\theta}) & = 1 - h_\theta(\bm{x}) \end{aligned} P(y=1∣x;θ)P(y=0∣x;θ)=hθ(x)=1−hθ(x)
即对于真实标记是 1 1 1的样本,我们希望预测值越接近于 1 1 1,损失越小;对于真实标记是 0 0 0的样本,我们希望预测值越接近于 0 0 0,损失越小。
(4)构造损失函数 J ( θ ) J(\boldsymbol{\theta}) J(θ)
我们都知道,评价一个模型好坏用的是损失函数,损失函数越小,就能说明模型越好。
最直观的想法是希望预测值与实际值尽可能接近,即看预测值与实际值之间的均方误差是否最小,所以定义线性回归损失函数为
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∥ h θ ( x ) − y ∥ 2 2 J(\boldsymbol{\theta}) = \frac{1}{2m}\sum_{i = 1}^{m} \left(h_\theta(\boldsymbol{x}^{(i)}) - y^{(i)}\right)^2 = \frac{1}{2m}\left \| h_\theta(\bm{x}) - \bm{y} \right \|_2^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1∥hθ(x)−y∥22
那么这个问题就变成了一个优化问题,即要找到令损失函数 J ( θ ) J(\bm{\theta}) J(θ)最小的 θ \bm{\theta} θ,很自然的,我们需要使用梯度下降法。
但是很不巧的是,这个函数不是凸函数,它的函数图形如下图所示。
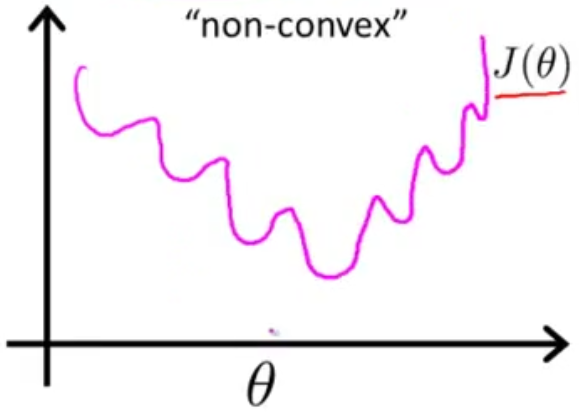
也就是说,这个函数我们如果使用梯度下降法,则很有可能在某一个局部凸函数的最小点停止,而不是整个函数的最小值点。所以我们不能使用均方差函数作为损失函数。
那么我们换个思路,跟据前面的推导, y y y只能取 0 0 0或 1 1 1,服从二项分布,则后验概率为
P ( y ∣ x ; θ ) = h θ ( x ) y ( 1 − h θ ( x ) ) 1 − y P(y \mid \bm{x}; \bm{\theta}) = h_\theta(\bm{x})^{y}\left(1 - h_\theta(\bm{x})\right)^{1 - y} P(y∣x;θ)=hθ(x)y(1−hθ(x))1−y
在这个式子中,无论 y = 0 y=0 y=0还是 y = 1 y=1 y=1, P ( y ∣ x ; θ ) P(y \mid \bm{x}; \bm{\theta}) P(y∣x;θ)的结果都是越趋近于1,模型预测能力越强。
那么我们就可以使用极大似然估计去求得 P ( y ∣ x ; θ ) P(y \mid \bm{x}; \bm{\theta}) P(y∣x;θ)的最大值,从而得到预测能力最好的模型。
对于 m m m个独立同分布的训练样本 x \bm{x} x,其似然函数 L ( θ ) L(\bm{\theta}) L(θ)为
L ( θ ) = ∏ i = 1 m P ( y ( i ) ∣ x ( i ) ; θ ) = ∏ i = 1 m h θ ( x ( i ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) \begin{aligned} L(\bm{\theta}) & = \prod_{i = 1}^{m}{P(y^{(i)} \mid \bm{x}^{(i)}; \bm{\theta})} \\ & = \prod_{i = 1}^{m}{h_\theta(\bm{x}^{(i)})^{y^{(i)}}\left(1 - h_\theta(\bm{x}^{(i)})\right)^{1 - y^{(i)}}} \end{aligned} L(θ)=i=1∏mP(y(i)∣x(i);θ)=i=1∏mhθ(x(i))y(i)(1−hθ(x(i)))1−y(i)
取对数,则对数似然函数 l ( θ ) l(\bm{\theta}) l(θ)为
l ( θ ) = log L ( θ ) = log ∏ i = 1 m P ( y ( i ) ∣ x ( i ) ; θ ) = ∑ i = 1 m log P ( y ( i ) ∣ x ( i ) ; θ ) = ∑ i = 1 m log [ h θ ( x ( i ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) ] = ∑ i = 1 m [ y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] \begin{aligned} l(\bm{\theta}) & = \log{L(\bm{\theta})} \\ & = \log{\prod_{i = 1}^{m}{P(y^{(i)} \mid \bm{x}^{(i)}; \bm{\theta})}} \\ & = \sum_{i = 1}^{m}\log{P(y^{(i)} \mid \bm{x}^{(i)}; \bm{\theta})} \\ & = \sum_{i = 1}^{m} {\log{\left[h_\theta(\bm{x}^{(i)})^{y^{(i)}}\left(1 - h_\theta(\bm{x}^{(i)})\right)^{1 - y^{(i)}}\right]}} \\ & = \sum_{i = 1}^{m} {\left[ y^{(i)} \log{h_\theta(\bm{x}^{(i)})} + \left(1 - y^{(i)}\right) \log{\left(1 - h_\theta(\bm{x}^{(i)})\right)} \right]} \end{aligned} l(θ)=logL(θ)=logi=1∏mP(y(i)∣x(i);θ)=i=1∑mlogP(y(i)∣x(i);θ)=i=1∑mlog[hθ(x(i))y(i)(1−hθ(x(i)))1−y(i)]=i=1∑m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
但是我们可以看出来,随着 h θ ( x ) h_\theta(\bm{x}) hθ(x)逐渐变得准确, P ( y ∣ x ; θ ) P(y \mid \bm{x}; \bm{\theta}) P(y∣x;θ)的值越来越趋近于 1 1 1,那么 l ( θ ) l(\bm{\theta}) l(θ)的值从 − ∞ -\infty −∞逐渐变为0,为单调递增函数。
那么定义损失函数为
J ( θ ) = − 1 m l ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] \begin{aligned} J(\boldsymbol{\theta}) & = -\frac{1}{m} l(\bm{\theta}) \\ & = -\frac{1}{m} \sum_{i = 1}^{m} {\left[ y^{(i)} \log{h_\theta(\bm{x}^{(i)})} + \left(1 - y^{(i)}\right) \log{\left(1 - h_\theta(\bm{x}^{(i)})\right)} \right]} \end{aligned} J(θ)=−m1l(θ)=−m1i=1∑m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
就可以实现损失函数是凸函数(见下图),从而可以使用梯度下降法去求 arg min θ J ( θ ) {\arg \underset{\bm{\theta}}{\mathop{\min}}}\,J(\bm{\theta}) argθminJ(θ).
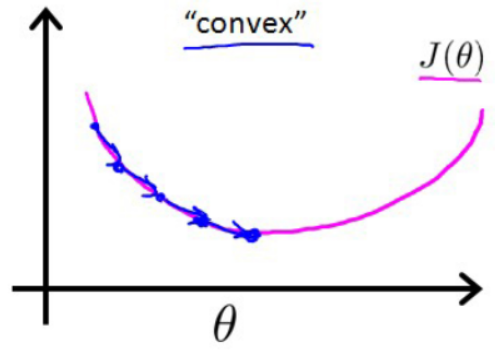
事实上,如果我们定义 C o s t Cost Cost函数为
C o s t ( h θ ( x ) , y ) = { − log h θ ( x ) , if y = 1 − log ( 1 − h θ ( x ) ) , if y = 0 Cost(h_\theta(x), y) = \begin{cases} -\log{h_\theta(x)} &,\ \text{if $y = 1$} \\ -\log{\left(1 - h_\theta(x)\right)} &,\ \text{if $y = 0$} \end{cases} Cost(hθ(x),y)={−loghθ(x)−log(1−hθ(x)), if y=1, if y=0
这个函数的图形如下图所示
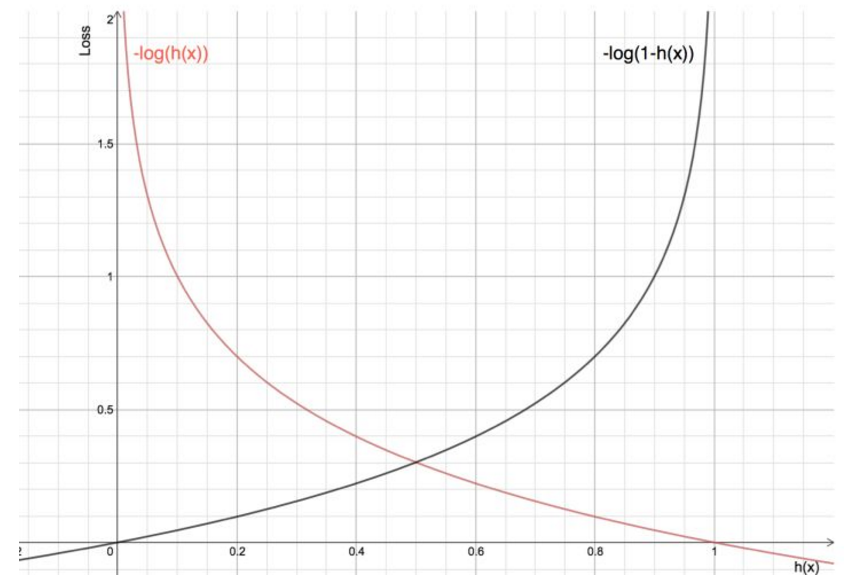
可以看到,随着 h ( x ) h(x) h(x)的增大, − log h ( x ) -\log{h(x)} −logh(x)逐渐由 ∞ \infty ∞降到 0 0 0; − log ( 1 − h ( x ) ) -\log{\left(1 - h(x)\right)} −log(1−h(x))逐渐由 0 0 0增到 ∞ \infty ∞,我们把这个 C o s t Cost Cost函数叫做交叉熵。
那么就有
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] \begin{aligned} J(\bm{\theta}) & = \frac{1}{m} \sum_{i = 1}^{m} Cost(h_\theta(\bm{x}^{(i)}), y^{(i)}) \\ & = -\frac{1}{m} \sum_{i = 1}^{m} {\left[ y^{(i)} \log{h_\theta(\bm{x}^{(i)})} + \left(1 - y^{(i)}\right) \log{\left(1 - h_\theta(\bm{x}^{(i)})\right)} \right]} \end{aligned} J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))=−m1i=1∑m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
但是如果我们的模型选取的太复杂的话,会造成过拟合的后果,所以我们还需要加上惩罚项来避免过拟合,则损失函数变为
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∥ θ ∥ 2 2 J(\bm{\theta}) = -\frac{1}{m} \sum_{i = 1}^{m} {\left[ y^{(i)} \log{h_\theta(\bm{x}^{(i)})} + \left(1 - y^{(i)}\right) \log{\left(1 - h_\theta(\bm{x}^{(i)})\right)} \right]} + \frac{\lambda}{2m} \left \| \bm{\theta} \right \|_2^2 J(θ)=−m1i=1∑m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλ∥θ∥22
(5)梯度下降法找最小值
因为损失函数 J ( θ ) J(\bm{\theta}) J(θ)满足凸函数的性质,所以可以与线性回归一样,使用梯度下降法来求解 arg min θ J ( θ ) {\arg \underset{\bm{\theta}}{\mathop{\min}}}\,J(\bm{\theta}) argθminJ(θ).
即
θ j ( n + 1 ) = θ j ( n ) − α ∂ J ( θ ) ∂ θ j ( n ) = θ j ( n ) − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] \begin{aligned} \theta_j^{(n+1)} & = \theta_j^{(n)} - \alpha \frac{\partial J(\bm{\theta})}{\partial \theta_j^{(n)}} \\ & = \theta_j^{(n)} - \alpha \left[ \frac{1}{m} \sum_{i = 1}^{m} \left(h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \right] \end{aligned} θj(n+1)=θj(n)−α∂θj(n)∂J(θ)=θj(n)−α[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
其中
∂ J ( θ ) ∂ θ j = − 1 m ∑ i = 1 m ( y ( i ) 1 h θ ( x ( i ) ) ∂ h θ ( x ( i ) ) ∂ θ j − ( 1 − y ( i ) ) 1 1 − h θ ( x ( i ) ) ∂ h θ ( x ( i ) ) ∂ θ j ) + λ m θ j = − 1 m ∑ i = 1 m ( y ( i ) 1 g ( θ T x ( i ) ) − ( 1 − y ( i ) ) 1 1 − g ( θ T x ( i ) ) ) ∂ g ( θ T x ( i ) ) ∂ θ j + λ m θ j = − 1 m ∑ i = 1 m ( y ( i ) 1 g ( θ T x ( i ) ) − ( 1 − y ( i ) ) 1 1 − g ( θ T x ( i ) ) ) g ( θ T x ( i ) ) ( 1 − g ( θ T x ( i ) ) ) ∂ ( θ T x ( i ) ) ∂ θ j + λ m θ j = − 1 m ∑ i = 1 m ( y ( i ) ( 1 − g ( θ T x ( i ) ) ) − ( 1 − y ( i ) ) g ( θ T x ( i ) ) ) x j ( i ) + λ m θ j = − 1 m ∑ i = 1 m ( y ( i ) − g ( θ T x ( i ) ) ) x j ( i ) + λ m θ j = − 1 m ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) + λ m θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j \begin{aligned} \frac{\partial J(\bm{\theta})}{\partial \theta_j} & = -\frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} \frac{1}{h_\theta(\bm{x}^{(i)})} \frac{\partial h_\theta(\bm{x}^{(i)})}{\partial \theta_j} - \left(1 - y^{(i)}\right) \frac{1}{1 - h_\theta(\bm{x}^{(i)})} \frac{\partial h_\theta(\bm{x}^{(i)})}{\partial \theta_j} \right) + \frac{\lambda}{m} \theta_j \\ & = -\frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} \frac{1}{g(\bm{\theta}^T \bm{x}^{(i)})} - \left(1 - y^{(i)}\right) \frac{1}{1 - g(\bm{\theta}^T \bm{x}^{(i)})} \right) \frac{\partial g(\bm{\theta}^T \bm{x}^{(i)})}{\partial \theta_j} + \frac{\lambda}{m} \theta_j \\ & = -\frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} \frac{1}{g(\bm{\theta}^T \bm{x}^{(i)})} - \left(1 - y^{(i)}\right) \frac{1}{1 - g(\bm{\theta}^T \bm{x}^{(i)})} \right) g(\bm{\theta}^T \bm{x}^{(i)}) \left( 1 - g(\bm{\theta}^T \bm{x}^{(i)}) \right) \frac{\partial \left( \bm{\theta}^T \bm{x}^{(i)} \right)}{\partial \theta_j} + \frac{\lambda}{m} \theta_j \\ & = -\frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} \left(1 - g(\bm{\theta}^T \bm{x}^{(i)}) \right) - \left(1 - y^{(i)}\right) g(\bm{\theta}^T \bm{x}^{(i)}) \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \\ & = -\frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} - g(\bm{\theta}^T \bm{x}^{(i)}) \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \\ & = -\frac{1}{m} \sum_{i = 1}^{m} \left( y^{(i)} - h_\theta(\bm{x}^{(i)}) \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \\ & = \frac{1}{m} \sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_j^{(i)} + \frac{\lambda}{m} \theta_j \end{aligned} ∂θj∂J(θ)=−m1i=1∑m(y(i)hθ(x(i))1∂θj∂hθ(x(i))−(1−y(i))1−hθ(x(i))1∂θj∂hθ(x(i)))+mλθj=−m1i=1∑m(y(i)g(θTx(i))1−(1−y(i))1−g(θTx(i))1)∂θj∂g(θTx(i))+mλθj=−m1i=1∑m(y(i)g(θTx(i))1−(1−y(i))1−g(θTx(i))1)g(θTx(i))(1−g(θTx(i)))∂θj∂(θTx(i))+mλθj=−m1i=1∑m(y(i)(1−g(θTx(i)))−(1−y(i))g(θTx(i)))xj(i)+mλθj=−m1i=1∑m(y(i)−g(θTx(i)))xj(i)+mλθj=−m1i=1∑m(y(i)−hθ(x(i)))xj(i)+mλθj=m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj
这里用到复合函数积分,若 f ( x ) = 1 1 + e − g ( x ) f(x) = \cfrac{1}{1 + e^{-g(x)}} f(x)=1+e−g(x)1,则
d f ( x ) d x = 1 ( 1 + e − g ( x ) ) 2 e − g ( x ) d g ( x ) d x = 1 1 + e − g ( x ) e − g ( x ) 1 + e − g ( x ) d g ( x ) d x = f ( x ) ( 1 − f ( x ) ) d g ( x ) d x \begin{aligned} \frac{\mathrm{d} f(x)}{\mathrm{d} x} & = \frac{1}{{\left(1 + e^{-g(x)} \right)}^2} e^{-g(x)} \frac{\mathrm{d} g(x)}{\mathrm{d} x} \\ & = \frac{1}{1 + e^{-g(x)}} \frac{e^{-g(x)}}{1 + e^{-g(x)}} \frac{\mathrm{d} g(x)}{\mathrm{d} x} \\ & = f(x) \left( 1 - f(x) \right) \frac{\mathrm{d} g(x)}{\mathrm{d} x} \end{aligned} dxdf(x)=(1+e−g(x))21e−g(x)dxdg(x)=1+e−g(x)11+e−g(x)e−g(x)dxdg(x)=f(x)(1−f(x))dxdg(x)
(6)向量化结果表示
上面已经推导出了梯度下降法的公式,现在我们对公式进行向量化。
记
x = ( x ( 1 ) x ( 2 ) ⋯ x ( m ) ) T y = ( y ( 1 ) y ( 2 ) ⋯ y ( m ) ) T \begin{aligned} \bm{x} &= \begin{pmatrix} \bm{x}^{(1)} & \bm{x}^{(2)} & \cdots & \bm{x}^{(m)} \end{pmatrix}^T \\ \bm{y} & = \begin{pmatrix} y^{(1)} & y^{(2)} & \cdots & y^{(m)} \end{pmatrix}^T \end{aligned} xy=(x(1)x(2)⋯x(m))T=(y(1)y(2)⋯y(m))T
其中
x ( i ) = ( x 0 ( i ) x 1 ( i ) ⋯ x n ( i ) ) T , i = 1 , 2 , ⋯ , m \bm{x}^{(i)} = \left( \begin{matrix} x_0^{(i)} & x_1^{(i)} & \cdots & x_n^{(i)} \end{matrix} \right)^T ,\quad i = 1, 2, \cdots, m x(i)=(x0(i)x1(i)⋯xn(i))T,i=1,2,⋯,m
则
∂ J ( θ ) ∂ θ = ( ∂ J ( θ ) ∂ θ 0 ∂ J ( θ ) ∂ θ 1 ⋮ ∂ J ( θ ) ∂ θ n ) = ( 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) + λ m θ 0 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) + λ m θ 1 ⋮ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x n ( i ) + λ m θ n ) = 1 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) ⋮ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x n ( i ) ) + λ m ( θ 0 θ 1 ⋮ θ n ) = 1 m ( ( x 0 ( 1 ) x 0 ( 2 ) ⋯ x 0 ( m ) ) ( h θ ( x ( 1 ) ) − y ( 1 ) h θ ( x ( 2 ) ) − y ( 2 ) ⋮ h θ ( x ( m ) ) − y ( m ) ) ( x 1 ( 1 ) x 1 ( 2 ) ⋯ x 1 ( m ) ) ( h θ ( x ( 1 ) ) − y ( 1 ) h θ ( x ( 2 ) ) − y ( 2 ) ⋮ h θ ( x ( m ) ) − y ( m ) ) ⋮ ( x n ( 1 ) x n ( 2 ) ⋯ x n ( m ) ) ( h θ ( x ( 1 ) ) − y ( 1 ) h θ ( x ( 2 ) ) − y ( 2 ) ⋮ h θ ( x ( m ) ) − y ( m ) ) ) + λ m θ = 1 m ( x 0 ( 1 ) x 0 ( 2 ) ⋯ x 0 ( m ) x 1 ( 1 ) x 1 ( 2 ) ⋯ x 1 ( m ) ⋮ ⋮ ⋱ ⋮ x n ( 1 ) x n ( 2 ) ⋯ x n ( m ) ) ( h θ ( x ( 1 ) ) − y ( 1 ) h θ ( x ( 2 ) ) − y ( 2 ) ⋮ h θ ( x ( m ) ) − y ( m ) ) + λ m θ = 1 m x T ( ( h θ ( x T ) ) T − y ) + λ m θ \begin{aligned} \cfrac{\partial J(\bm{\theta})}{\partial \bm{\theta}} & = \begin{pmatrix} \cfrac{\partial J(\bm{\theta})}{\partial \theta_0} \\ \cfrac{\partial J(\bm{\theta})}{\partial \theta_1} \\ \vdots \\ \cfrac{\partial J(\bm{\theta})}{\partial \theta_n} \end{pmatrix} \\ & = \begin{pmatrix} \cfrac{1}{m} \displaystyle\sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_0^{(i)} + \cfrac{\lambda}{m} \theta_0 \\ \cfrac{1}{m} \displaystyle\sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_1^{(i)} + \cfrac{\lambda}{m} \theta_1 \\ \vdots \\ \cfrac{1}{m} \displaystyle\sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_n^{(i)} + \cfrac{\lambda}{m} \theta_n \end{pmatrix} \\ & = \frac{1}{m} \begin{pmatrix} \displaystyle\sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_0^{(i)} \\ \displaystyle\sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_1^{(i)} \\ \vdots \\ \displaystyle\sum_{i = 1}^{m} \left( h_\theta(\bm{x}^{(i)}) - y^{(i)} \right) x_n^{(i)} \end{pmatrix} +\frac{\lambda}{m} \begin{pmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{pmatrix} \\ & = \frac{1}{m} \begin{pmatrix} \begin{pmatrix} x_0^{(1)} & x_0^{(2)} & \cdots & x_0^{(m)} \end{pmatrix} \begin{pmatrix} h_\theta(\bm{x}^{(1)}) - y^{(1)} \\ h_\theta(\bm{x}^{(2)}) - y^{(2)} \\ \vdots \\ h_\theta(\bm{x}^{(m)}) - y^{(m)} \end{pmatrix} \\ \begin{pmatrix} x_1^{(1)} & x_1^{(2)} & \cdots & x_1^{(m)} \end{pmatrix} \begin{pmatrix} h_\theta(\bm{x}^{(1)}) - y^{(1)} \\ h_\theta(\bm{x}^{(2)}) - y^{(2)} \\ \vdots \\ h_\theta(\bm{x}^{(m)}) - y^{(m)} \end{pmatrix} \\ \vdots \\ \begin{pmatrix} x_n^{(1)} & x_n^{(2)} & \cdots & x_n^{(m)} \end{pmatrix} \begin{pmatrix} h_\theta(\bm{x}^{(1)}) - y^{(1)} \\ h_\theta(\bm{x}^{(2)}) - y^{(2)} \\ \vdots \\ h_\theta(\bm{x}^{(m)}) - y^{(m)} \end{pmatrix} \end{pmatrix} +\frac{\lambda}{m} \bm{\theta} \\ & = \frac{1}{m} \begin{pmatrix} x_0^{(1)} & x_0^{(2)} & \cdots & x_0^{(m)} \\ x_1^{(1)} & x_1^{(2)} & \cdots & x_1^{(m)} \\ \vdots & \vdots & \ddots & \vdots\\ x_n^{(1)} & x_n^{(2)} & \cdots & x_n^{(m)} \end{pmatrix} \begin{pmatrix} h_\theta(\bm{x}^{(1)}) - y^{(1)} \\ h_\theta(\bm{x}^{(2)}) - y^{(2)} \\ \vdots \\ h_\theta(\bm{x}^{(m)}) - y^{(m)} \end{pmatrix} +\frac{\lambda}{m} \bm{\theta} \\ & = \frac{1}{m} \bm{x}^T \begin{pmatrix} \begin{pmatrix} h_\theta(\bm{x}^T) \end{pmatrix}^T -\bm{y} \end{pmatrix} +\frac{\lambda}{m} \bm{\theta} \end{aligned} ∂θ∂J(θ)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛∂θ0∂J(θ)∂θ1∂J(θ)⋮∂θn∂J(θ)⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛m1i=1∑m(hθ(x(i))−y(i))x0(i)+mλθ0m1i=1∑m(hθ(x(i))−y(i))x1(i)+mλθ1⋮m1i=1∑m(hθ(x(i))−y(i))xn(i)+mλθn⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=m1⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛i=1∑m(hθ(x(i))−y(i))x0(i)i=1∑m(hθ(x(i))−y(i))x1(i)⋮i=1∑m(hθ(x(i))−y(i))xn(i)⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞+mλ⎝⎜⎜⎜⎛θ0θ1⋮θn⎠⎟⎟⎟⎞=m1⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛(x0(1)x0(2)⋯x0(m))⎝⎜⎜⎜⎛hθ(x(1))−y(1)hθ(x(2))−y(2)⋮hθ(x(m))−y(m)⎠⎟⎟⎟⎞(x1(1)x1(2)⋯x1(m))⎝⎜⎜⎜⎛hθ(x(1))−y(1)hθ(x(2))−y(2)⋮hθ(x(m))−y(m)⎠⎟⎟⎟⎞⋮(xn(1)xn(2)⋯xn(m))⎝⎜⎜⎜⎛hθ(x(1))−y(1)hθ(x(2))−y(2)⋮hθ(x(m))−y(m)⎠⎟⎟⎟⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞+mλθ=m1⎝⎜⎜⎜⎜⎛x0(1)x1(1)⋮xn(1)x0(2)x1(2)⋮xn(2)⋯⋯⋱⋯x0(m)x1(m)⋮xn(m)⎠⎟⎟⎟⎟⎞⎝⎜⎜⎜⎛hθ(x(1))−y(1)hθ(x(2))−y(2)⋮hθ(x(m))−y(m)⎠⎟⎟⎟⎞+mλθ=m1xT((hθ(xT))T−y)+mλθ
在这里,如果我们记
A = x ⋅ θ = ( x 0 ( 1 ) x 1 ( 1 ) ⋯ x n ( 1 ) x 0 ( 2 ) x 1 ( 2 ) ⋯ x n ( 2 ) ⋮ ⋮ ⋱ ⋮ x 0 ( m ) x 1 ( m ) ⋯ x n ( m ) ) ⋅ ( θ 0 θ 1 ⋮ θ n ) \begin{aligned} \bm{A} & = \bm{x} \cdot \bm{\theta} \\ & = \begin{pmatrix} x_0^{(1)} & x_1^{(1)} & \cdots & x_n^{(1)} \\ x_0^{(2)} & x_1^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots\\ x_0^{(m)} & x_1^{(m)} & \cdots & x_n^{(m)} \end{pmatrix} \cdot \begin{pmatrix} \theta_0 \\ \theta_1 \\ \vdots\\ \theta_n \end{pmatrix} \end{aligned} A=x⋅θ=⎝⎜⎜⎜⎜⎛x0(1)x0(2)⋮x0(m)x1(1)x1(2)⋮x1(m)⋯⋯⋱⋯xn(1)xn(2)⋮xn(m)⎠⎟⎟⎟⎟⎞⋅⎝⎜⎜⎜⎛θ0θ1⋮θn⎠⎟⎟⎟⎞
则很容易地,我们可以做代换
( h θ ( x T ) ) T = h θ ( A ) \begin{pmatrix} h_\theta(\bm{x}^T) \end{pmatrix}^T = h_\theta(\bm{A}) (hθ(xT))T=hθ(A)
那么
∂ J ( θ ) ∂ θ = 1 m x T ( h θ ( A ) − y ) + λ m θ \cfrac{\partial J(\bm{\theta})}{\partial \bm{\theta}} = \frac{1}{m} \bm{x}^T \begin{pmatrix} h_\theta(\bm{A}) - \bm{y} \end{pmatrix} +\frac{\lambda}{m} \bm{\theta} ∂θ∂J(θ)=m1xT(hθ(A)−y)+mλθ
所以在迭代的时候,我们有
θ ( p + 1 ) = θ ( p ) − α ∂ J ( θ ( p ) ) ∂ θ ( p ) = θ ( p ) − α m [ x T ( h θ ( A ) − y ) + λ θ ( p ) ] \begin{aligned} \bm{\theta}^{(p+1)} & = \bm{\theta}^{(p)} - \alpha \cfrac{\partial J(\bm{\theta}^{(p)})}{\partial \bm{\theta}^{(p)}} \\ & = \bm{\theta}^{(p)} - \frac{\alpha}{m} \left[ \bm{x}^T \begin{pmatrix} h_\theta(\bm{A}) - \bm{y} \end{pmatrix} +\lambda \bm{\theta}^{(p)} \right] \end{aligned} θ(p+1)=θ(p)−α∂θ(p)∂J(θ(p))=θ(p)−mα[xT(hθ(A)−y)+λθ(p)]
如此,变完成了梯度下降法的向量转化。
三、代码实现
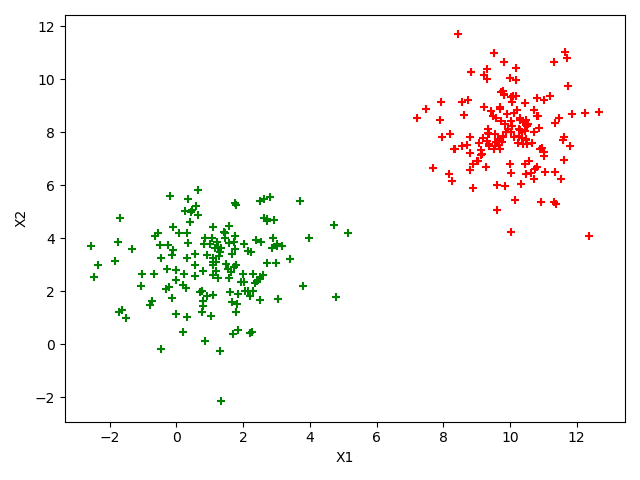
1. 构造数据
本次构造数据采用二维高斯分布构造数据,构造满足朴素贝叶斯的数据,即协方差矩阵是对角矩阵的数据。
构造出来的数据如下图所示(满足朴素贝叶斯假设)。
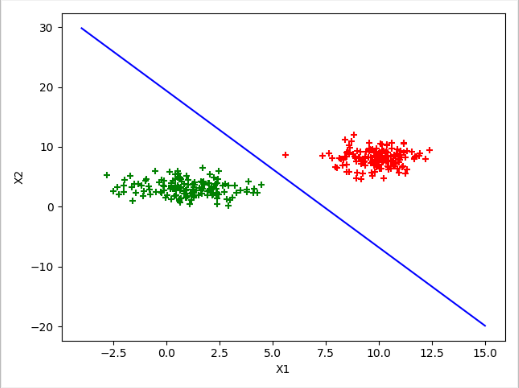
2. 实现逻辑回归分类
按照上面所讲的算法进行分类,最终得到如下图所示的分类效果, J ( θ ) J(\bm{\theta}) J(θ)经过训练,最终降到 0.000489596368502944 0.000489596368502944 0.000489596368502944, θ \bm{\theta} θ的值为 ( − 18.09239552 2.61418602 0.66697504 ) \begin{pmatrix} -18.09239552 & 2.61418602 & 0.66697504 \end{pmatrix} (−18.092395522.614186020.66697504)
3. 代码(Python实现)
import numpy as np
import matplotlib.pyplot as plt
# 构造符合独立性的二维高斯分布的数据点
def create_data(mu1, mu2, sigma1, sigma2, size):
mean = np.array([mu1, mu2])
cov = np.diag([sigma1, sigma2])
f1 = np.random.multivariate_normal(mean, cov, size)
X1 = f1[:, 0]
X2 = f1[:, 1]
return X1, X2
# Sigmoid函数
def sigmoid(z):
return 1.0 / (1 + np.exp(-z))
# 计算损失函数
def loss(X, Y, theta, lamda, size):
X = np.array(X)
Y = np.array(Y)
theta = np.array(theta)
res = 0
for i in range(size):
z = np.dot(theta.T, X[i])
res = res + Y[i] * np.log(sigmoid(z)) + (1 - Y[i]) * np.log(1 - sigmoid(z))
res = -res / size
res = res + lamda / (2 * size) * np.dot(theta.T, theta)
return res
# 梯度下降法
def gradient_method(X, Y, theta, lamda, alpha, size):
X = np.array(X)
Y = np.array(Y)
theta = np.array(theta)
error1 = loss(X, Y, theta, lamda, size)
times = 0
while True:
tmp = []
for i in range(size):
tmp.append(sigmoid(np.dot(theta.T, X[i]))-Y[i])
tmp = np.array(tmp)
gra = np.dot(X.T, tmp) + lamda * theta
gra = gra / size
theta = theta - alpha * gra
times += 1
if times == 1000:
error2 = loss(X, Y, theta, lamda, size)
if error1 - error2 < 0.000001:
break
error1 = error2
times = 0
print(error1)
return theta
# 主函数
if __name__ == '__main__':
X11, X12 = create_data(10, 8, 1, 2, 150)
X21, X22 = create_data(1, 3, 2, 1.5, 150)
X = []
X0 = np.ones(300)
X1 = np.concatenate([X11, X21], axis=0)
X2 = np.concatenate([X12, X22], axis=0)
X.append(X0)
X.append(X1)
X.append(X2)
X = np.array(X).T
Y1 = np.ones(150)
Y2 = np.zeros(150)
Y = np.concatenate([Y1, Y2], axis=0)
theta = np.array([-18.0544146, 2.78338406, 0.79579366])
theta = np.array(gradient_method(X, Y, theta, 0.0005, 0.001, 300))
print(theta)
x = np.linspace(-4, 15, 1000)
y = [-theta[1] / theta[2] * a - theta[0] / theta[2] for a in x]
plt.scatter(X11, X12, c='r', marker='+')
plt.scatter(X21, X22, c='g', marker='+')
plt.plot(x, y, color='b')
plt.xlabel("X1")
plt.ylabel("X2")
plt.show()























 2432
2432











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










