comsol纳米摩擦发电机数值模拟计算，在两个电极表面感应异种的电荷密度

comsol纳米摩擦发电机数值模拟计算，在两个电极表面感应异种的电荷密度，得到不同电极间距下的电势和电场分布

标题：基于COMSOL的纳米摩擦发电机数值模拟计算

摘要：
纳米摩擦发电机是一种利用微小摩擦力产生电能的新兴能量转换装置，具有结构简单、易于制备和高能量转换效率等优点。本文通过使用COMSOL软件进行纳米摩擦发电机的数值模拟计算，研究了在不同电极间距下的电势和电场分布。通过得到电荷密度的分布情况，为进一步优化纳米摩擦发电机的性能提供了理论依据。

1. 引言
随着能源危机的加剧和清洁能源需求的增长，纳米能源技术作为一种绿色、高效的能量转换方式备受关注。纳米摩擦发电机作为一种新兴的纳米能量转换装置，通过利用微小摩擦力产生电能，具有广阔的应用前景。

2. 研究背景
纳米摩擦发电机的核心原理是通过电极表面的摩擦作用产生电势差，从而产生电流。然而，为了进一步提高纳米摩擦发电机的能量转换效率，需要深入研究在不同电极间距下的电势和电场分布情况。因此，数值模拟计算成为了研究的一种重要手段。

3. 研究方法
本文采用COMSOL软件对纳米摩擦发电机进行数值模拟计算。首先，建立纳米摩擦发电机的几何模型，包括电极、摩擦层和载荷。然后，通过设置合适的边界条件和材料参数，模拟计算出在不同电极间距下的电势和电场分布情况。

4. 结果与分析
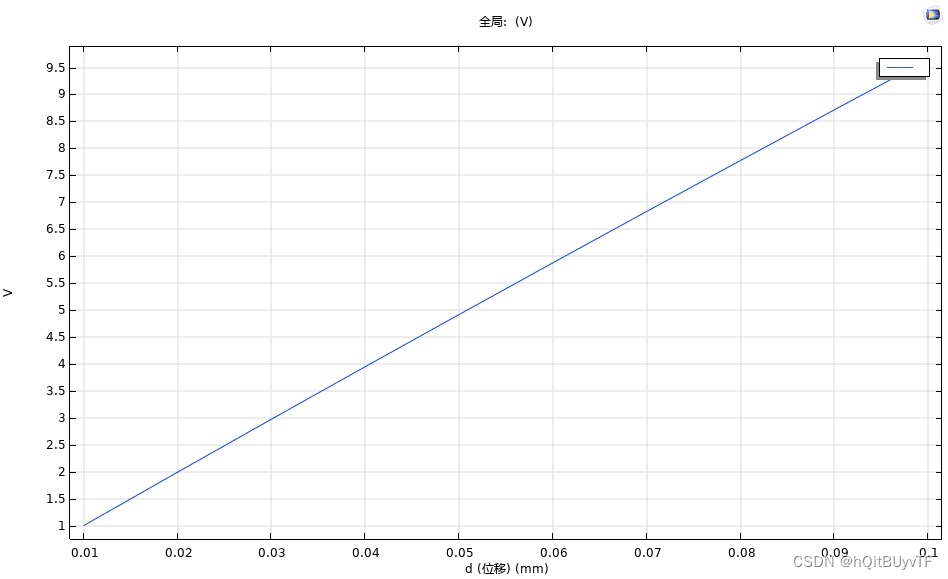
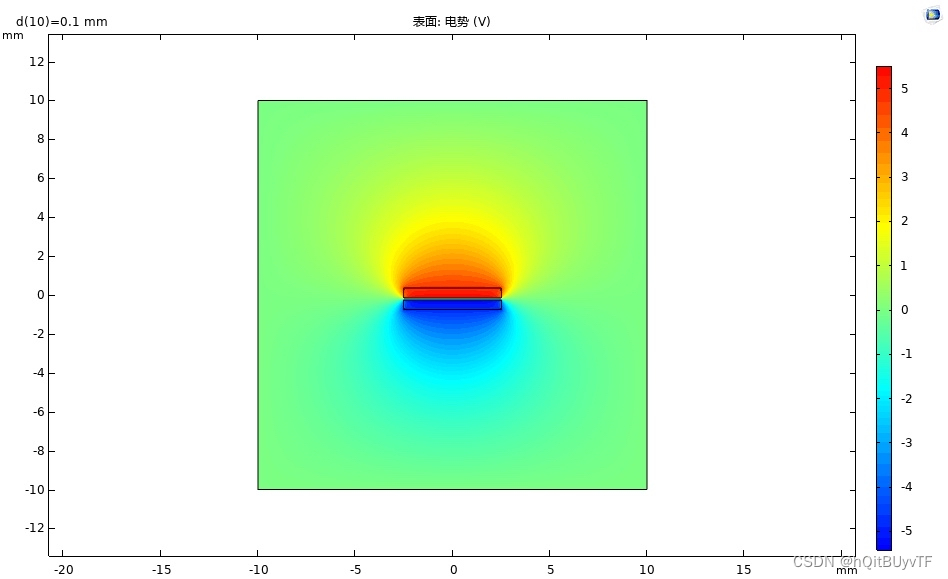
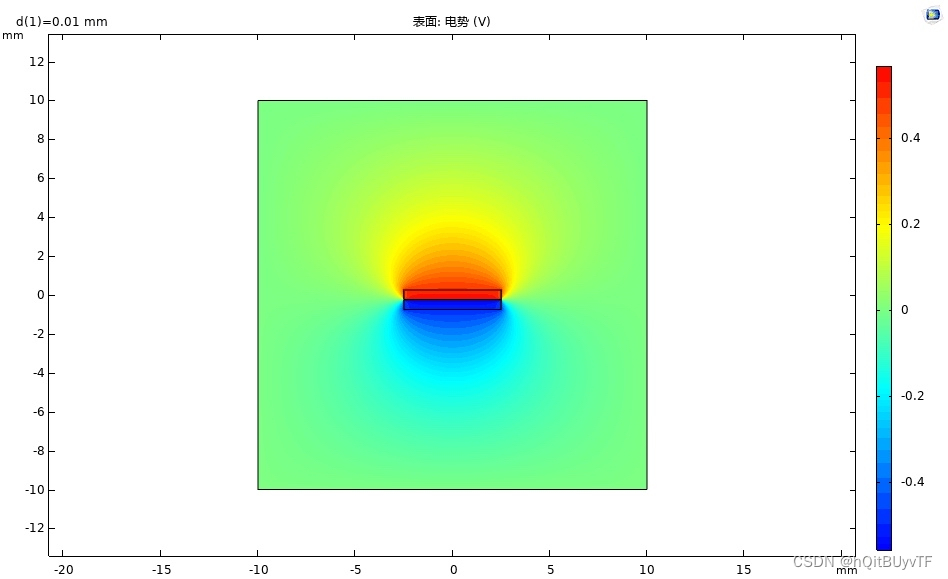
通过数值模拟计算，得到了不同电极间距下的电势和电场分布情况。分析结果表明，随着电极间距的增加，电势差逐渐减小，电场强度也逐渐减小。这说明电极间距对纳米摩擦发电机的能量转换效率具有重要影响。

5. 应用前景与展望
纳米摩擦发电机作为一种新兴的纳米能量转换装置，具有广阔的应用前景。通过深入研究在不同电极间距下的电势和电场分布情况，可以为优化纳米摩擦发电机的性能提供理论依据，并进一步推动其在可穿戴设备、传感器和智能物联网等领域的应用。

结论：
本文通过使用COMSOL软件进行纳米摩擦发电机的数值模拟计算，研究了在不同电极间距下的电势和电场分布。数值模拟结果表明，电极间距对纳米摩擦发电机的能量转换效率具有影响。通过深入研究和优化，纳米摩擦发电机在可穿戴设备、传感器和智能物联网等领域的应用前景将更加广阔。本研究为进一步优化纳米摩擦发电机的性能提供了理论基础。

关键词：纳米摩擦发电机；数值模拟计算；COMSOL；电势分布；电场分布。

相关代码,程序地址：http://lanzoup.cn/674742797541.html