在实际环境中预测玩家流失

I. 引言

在过去的五年中，行为分析在评估和理解玩家行为方面的应用已从边缘走向了商业和学术游戏开发的核心组成部分。这一发展有几个原因，但总体上与移动设备方面的技术进步结合在一起；商业模式的变化使得游戏越来越多地在线发布，并打破了传统的基于零售的收入模式。在免费游戏 (Free-to-Play, F2P) 中，收入主要由广告和游戏内购买驱动。因此，监控、分析和预测玩家行为的能力对建立可持续的业务至关重要 [1]-[3]。

考虑到与当代游戏开发相关的市场和商业智能问题，特别是针对在线和移动平台的开发，成功的一个最重要因素是检测和定义未来某个时间会离开系统（例如游戏玩家）的订阅者的能力。这种类型的分析称为流失分析或流失预测。任何离开服务的订阅者、用户或 - 在游戏的情况下，玩家 - 通常被称为“流失者”，而流失者与非流失者的比率作为时间的函数决定了流失率 [4]。在F2P游戏中，流失率通常很高，频率分布严重偏斜，通常大多数玩家在游戏的前几分钟内就会离开 [1]-[3], [5]。这强调了预测玩家流失的兴趣，不仅是为了检测离开或越来越不感兴趣的玩家 - 这些玩家在最初招募时成本越来越高 - 以便启动激励他们留在游戏中的协议，还为了最大化收入，特别是在应用内购买 (IAP) 的情况下。留存和货币化是衡量游戏成功的两个不同但在实践中往往紧密相关的指标 [2], [3], [6]。

在本研究中，我们重点预测五款移动/社交F2P游戏中的流失。我们概述了在游戏中进行流失预测的挑战，并定义了用于流失预测的行为特征 [7], [8]。在提出不同的流失模型后，我们使用保留可能性的统计模型和非线性行为函数的组合，捕捉五款不同游戏中的玩家参与行为。

A. 贡献

随着大量游戏转向F2P，即“增值服务”收入模式，预测流失者已成为游戏数据挖掘和游戏分析中的关键挑战。据我们所知，与 [9] 一起，本工作在几个方面是世界首次：1) 这是首次使用来自F2P游戏的多游戏遥测数据集进行学术研究；2) 这是首次在多个游戏中进行流失预测；3) 这是首次仅使用与游戏无关的特征进行预测；4) 这是首次正式定义游戏中的流失，并使用不同的流失定义来评估流失，这些定义都基于游戏设计；5) 本工作是最早考虑流失预测而非流失描述的工作之一。除了工作的新颖性外，本文有三个主要贡献，如下所示：1) 我们识别并正式定义了需要通用模型的交互系统的流失预测问题，这些模型可以有效参数化。这包括两种数据提取方法和两种不同的问题定义，这些定义符合移动/F2P或社交游戏的行业标准。两种不同的流失定义 - 紧窗口和松窗口 - 被评估，而不仅仅是将流失视为玩家最后一次被看到的时间。这有助于处理跨游戏流失剖面不同的情况，或游戏设计的性质或分配给玩家的价值方式（例如基于总购买量的价值 vs. 社交价值）意味着不同的流失定义是相关的。这里的重点是流失预测，而不是如何激励玩家留存。松弛流失，或软流失，例如，认为流失是一个需要许多天甚至几周的渐进过程。使用软流失的优势在于它允许监控导致玩家流失的过程。2) 我们引入并定义了一组通用行为特征，使流失预测适用于广泛的F2P（及其他）游戏。值得注意的是，最重要的特征集中在用户参与度上，因此独立于实际的游戏内容。需要注意的是，以前的工作主要依赖于与游戏特定特征相关的行为特征来实现高精度预测（见下文相关工作）。3) 我们在五款不同的F2P游戏上评估了训练模型，达到了高预测准确度。预测准确度与之前发布的针对特定游戏的少数解决方案相匹配或超过。需要注意的是，我们无法在相关工作的数据上验证我们的模型，因为用于此类研究的数据集通常是专有的。

B. 相关工作

在F2P游戏中，分析是管理和优化设计及货币化的基础 [1]-[3]。在学术界，行为数据挖掘有着悠久的历史，但在数字游戏的具体背景下，这一研究方向历来是游戏AI [10]-[12] 或网络分析 [13], [14] 的重点。然而，随着分析、用户研究和商业智能实践在游戏行业的快速普及，玩家行为也成为更广泛研究的主题，涵盖了例如学习、影响评估、决策、行为分析、预测、留存、流失和参与 [15], [16]，以及在游戏开发过程中的整合、分析过程的管理等；所有这些的总体目标都是为游戏开发提供信息，无论是为了优化用户体验、参与度、货币化、学习等 [1]。

我们在此重点关注直接或间接使用行为分析进行流失分析的出版物。流失分析最近才在游戏背景中被采用，但在各种学科中已经研究了几十年。这尤其包括零售银行 [4]、保险 [17]、电信 [7], [18], [19]、在线广告 [20] 和社区问答平台 [8]。

在数字游戏的具体背景下，大多数关于流失预测和相关主题（如留存）的工作通常使用关于玩家的累积信息并在单一环境中预测流失，而不普遍定义流失者。此外，使用的数据集通常来自单个游戏，而不是构建适用于多个游戏的模型。一个重要的原因是行为遥测的机密性和价值性，这导致学术研究人员通常缺乏可用的工业数据 [6]。

重要的例外包括 [14]，他们调查了现在已停运的GameSpy服务中前50款游戏的受欢迎程度，使用每日平均玩家数并注意到幂律分布。Bauckhage等人 [21] 使用生命周期分析对五款主要商业游戏中的玩家参与进行了建模。将玩家的兴趣建模为一个隐藏变量，Bauckhage等人提取了游戏时间信息，并展示了如何用生命周期分布及其对应的过程来表示兴趣。正如 [14] 所指出的，结果表明玩家的兴趣随时间以幂律方式减少，尽管Bauckhage等人 [21] 更进一步解释了为什么会出现这种模式。

另一个例子是Weber等人 [22]，他们通过回归建模分析了一款足球游戏中留存与游戏内特征之间的相关性，以识别对玩家留存最有影响的特征。Kawale等人 [16] 专注于MMORPG EverQuest II，使用社交网络的扩散模型结合游戏时间分布建模，研究玩家在游戏中的社交影响与流失之间的关系。然而，获得的精度和召回率在最好的情况下约为50%，这可能表明应探索不同的分类器。Borbora等人 [15] 也使用来自EverQuest II的数据，采用混合（监督和无监督）方法预测流失。他们将流失者定义为取消游戏订阅或2个月内未活跃的人。提取了不同的游戏特征以及元数据信息，如玩家拥有的角色数量等，以学习一个二元决策函数，确定玩家是否会流失。

关于游戏留存和流失的研究有很大一部分来自网络科学，其目标是了解网络条件对服务质量和玩家满意度的影响。典型的研究游戏类型是大型多人在线角色扮演游戏 (MMORPG)，数据可以通过挖掘客户端-服务器流获得。为列出一些与当前工作相关的例子，Pittman和Gauthier [23] 挖掘了来自两个MMORPG（魔兽世界和战锤在线）各一个服务器的客户端-服务器流，重点测量和建模玩家分布、会话长度和玩家在虚拟世界中的移动，以为MMORPG服务器架构提供信息。他们检查了会话长度和到达/离开率，得出结论认为这两款MMORPG都经历了显著的流失，流失被理解为玩家加入和离开服务器，而不一定是游戏本身。Feng等人 [13] 将流量分析应用于MMORPG EVE Online的遥测数据。所使用的数据集涵盖了游戏从2003年至2006年的早期历史。得出了一些结论。例如，作者检查了玩家按月加入和退出游戏的比率，发现对于EVE Online，加入和离开的比率紧密相随，但玩家数量逐渐增加，从2003年中期的几千人增加到2005年末的15万人。作者得出结论认为玩家流失随时间增加，推测原因可能是新玩家在游戏中相对于现有玩家处于劣势，而这种劣势随着时间的推移而增加。

II. 流失预测

在以下内容中，我们将流失预测视为一个二元分类任务，即将每个玩家分类为流失或返回。分类器在已观测到的玩家的标记数据上进行训练，但当然需要目标玩家的实际数据进行预测。因此，给定某一时间点之前的玩家信息（此后称为截止日期），分类器决定玩家是否已经流失或将返回。在流失预测任务的第一个也是最直接的解释中，我们认为在截止日期之后没有单一会话的玩家为流失玩家。我们将这个问题定义称为P1。见图1（左），这些玩家标记为绿色，而返回的玩家标记为红色。P1只允许对流失玩家做出非常严厉的决定，这在现实应用中不是很有用，因为没有剩余的游戏会话，重新激活相关玩家的机会非常低（至少在游戏内）。为了放宽这个定义，使其更适用于现实环境，我们可以将截止日期后会话或游戏天数较少的玩家标记为流失者（软流失）。剩余的游戏天数必须落在一个大小为 $\frac{d}{r}$ 的滑动窗口范围内。这种放宽可以解释为对参与和不再参与的玩家的区分，而不是对流失和未流失玩家的更严格区分。从行业角度来看，这种区分是有价值的，因为那些可能很快就会停止游戏的玩家更容易接触并可能激励他们留在游戏中，而已经离开的玩家则更难接触和激励。我们将这种放宽的问题定义称为P2。图1（右）显示了P2的一个示例，并允许对P1和P2进行比较。

III. 数据预处理

本文中我们考虑的数据包含了GameAnalytics（www.gameanalytics.com）提供的五款不同游戏中玩家行为的观测数据。数据是在2013年五个月的时间内收集的。总共，我们分析了大约两千万次游戏会话。数据被标准化处理，以便与游戏内容相关的特征被丢弃。主要的特征表示围绕会话进行。如果适用，添加了额外的信息（例如，游戏内购买）。请注意，这并不违反游戏内容独立流失预测的基本理念，因为游戏内货币化现如今是很常见的。我们进行了某些标准的数据清理程序（例如，我们丢弃了可能错误的数据，如某用户在几秒钟内启动了成千上万次会话）。请注意，并非所有五款游戏都跨越相同的时间段或相同的生命周期。例如，我们不能观察到每款游戏用户基数的增加，而是这些游戏已经开始时就有大量的日活跃用户。此外，一些游戏仍然有忠实的用户群，因此尚未观察到用户数量的显著减少。虽然这确实使分类任务更加困难（也使得结果更难比较），但这是一种相当常见的情况。由于保密原因，我们不能提供关于这些游戏的更详细信息，也不能透露游戏的名称。

A. 数据生成

在以下内容中，我们将流失玩家的类别表示为TRUE，返回玩家的类别表示为FALSE。由于我们考虑监督分类任务，现在的任务是构建能够正确预测一组测试数据的相应类别标签的模型。然而，决定一个玩家被认为离开游戏的缺席时间 $d_{chrn}$（以天为单位）是至关重要的。对于实际应用，生成训练和测试数据是关键的，并直接影响分类器在实时数据中的准确性。我们采用了两种方法来生成数据。第一种方法是更经典/直接的数据生成方法，而第二种方法则更优化于现实应用，例如，供游戏开发者定期使用更新的模型预测玩家流失。

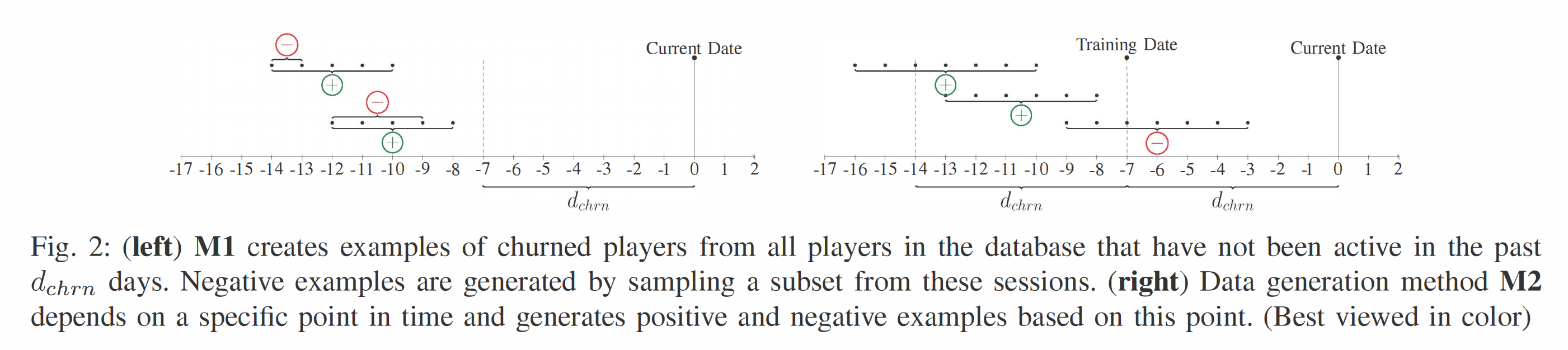
(M1) 生成训练样本的最简单方法是查看所有流失玩家，并将其视为正例。为了生成负例，我们从所有玩过不止一次会话的玩家中抽样。我们从第一次会话开始，随机选择一个截止会话。这组会话定义了一个负例，因为该玩家将来还会有会话。此过程如图2（左）所示。这种方法允许快速生成大数据集，并且可以通过丢弃数据来平衡正负类。然而，正如我们在实证评估中所见，许多用户只玩一次游戏，因此不能用于生成负例。请注意，这种生成训练数据的方法在现实环境中难以应用，因为假定无论当前日期如何，玩家的所有数据都是可用的。然而，由于它是直截了当的，并且在科学文献中更为常见，我们决定将其包括在内。

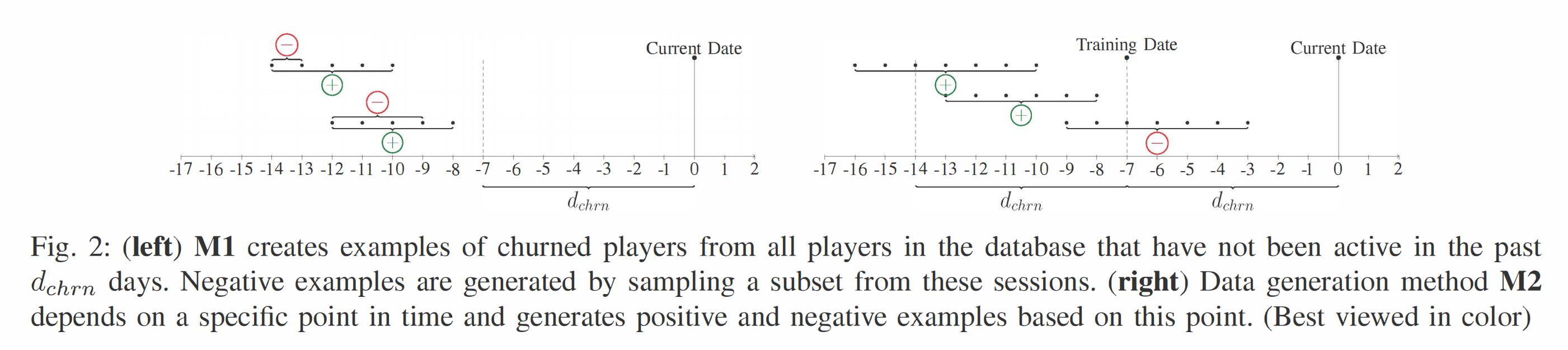
(M2) 另一种生成数据的方法是只考虑在特定范围内的会话。这种方法在选定的一天和一个 $d_{chrn}$ 天的时间窗口内查看玩家。这个训练日如图2（右）所示，虚线位于当前日期的左侧。FALSE示例是所有在此时登录并将在未来返回的玩家，即在当前日期和其左侧虚线之间的时间内。然而，生成足够数量的TRUE示例稍微复杂一些。一个简单的方法是考虑训练日之前窗口内的所有玩家，这些玩家不会返回。不幸的是，这可能导致高度不平衡的数据集，因为正例数量增加得比负例数量快得多（假设我们随时间推进窗口）。因此，我们为正例定义了一个额外的滑动窗口，并且只考虑该窗口内的数据。我们再次使用 $d_{chrn}$ 天，这个点由图2（右）中的最左虚线表示。我们使用这个窗口大小，因为在训练日之前仅在此日期之前活跃的所有玩家已被视为流失者。与M1不同，我们可以轻松地将缺席时间（即自上次会话以来的时间）作为描述玩家行为的特征（请注意，对于M1这也是可能的，但这需要另一个日期的抽样作为参考缺席日，从而增加了额外的复杂性）。由于我们只考虑滑动窗口内的玩家，这个缺席时间被限制在 $d_{chrn}$ 天内。在后面的评估中，我们通过随机选择滑动窗口中心日期来定义训练和测试数据，使用该时间点之前的数据。例如，一个可能的训练日期是测试日期前 $d_{chrn}$ 天。在实时系统中，最新的分类器将使用训练日 $d_{chrn}$ 天前的数据进行训练。因此，分类器会随时间变化，从而反映游戏内容或用户基数的变化。

B. 数据统计

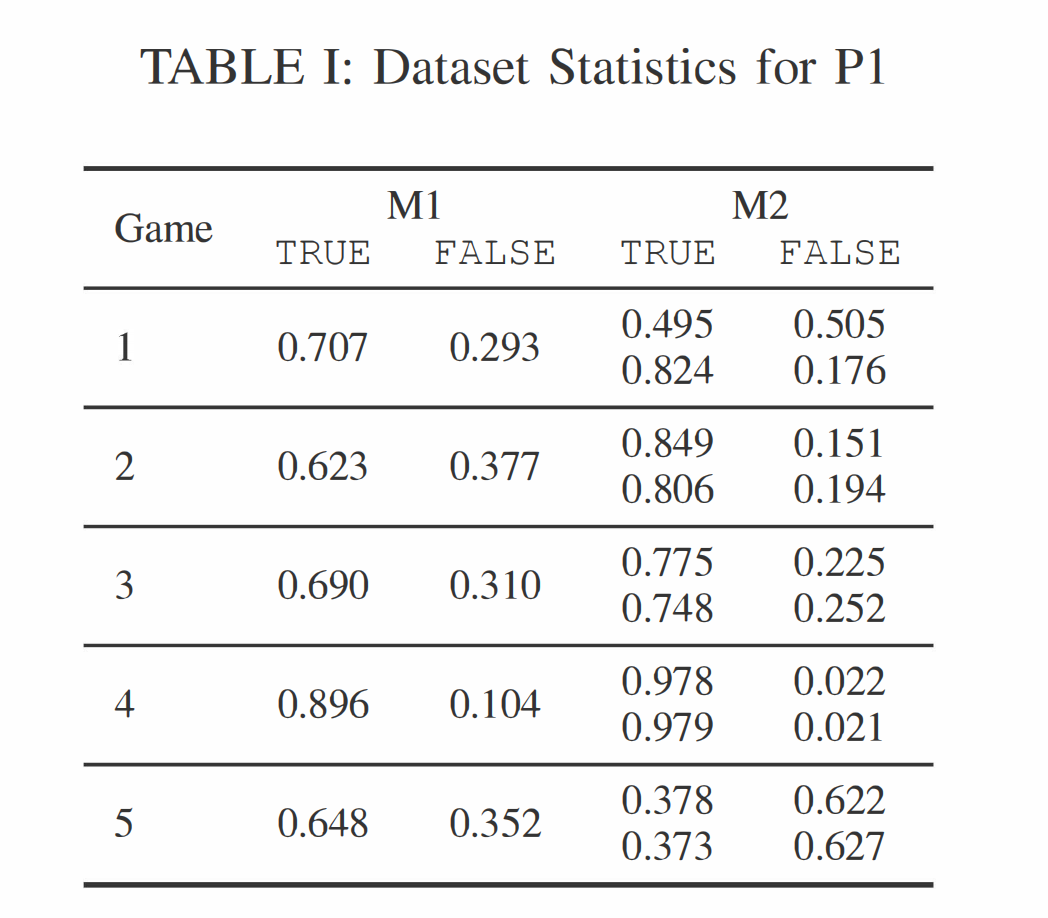
我们为每个游戏生成了一个基于方法 M1 的数据集，该数据集包含 50,000 名随机选择的用户。使用方法 M2，我们为每个游戏在不同日期生成了训练和测试数据集。如上所述，M2 围绕特定时间点工作，我们选择这些日期，使得训练和测试日期之间有 $d_{chrn}$ 天。在我们所有的实验中，我们设置 $d_{chrn}=7$。我们选择 7 这个值是因为我们在数据中观察到，超过 95% 的缺席时间在这个窗口内，并且它包含了一周的完整周期，包括每个工作日。生成的训练和测试数据集的大小取决于每个游戏在使用时间段内的活跃玩家数量，因此有所不同。然而，我们确保每个测试数据集都有数万名玩家用于评估。

表 I 和表 II 显示了五款游戏中标记为 TRUE（流失）和 FALSE（未流失）玩家的分布。对于每个游戏，第一行呈现训练数据集的统计数据，第二行呈现测试数据的统计数据。我们可以看到（总体上）M1 导致了更多的流失玩家而不是返回玩家。这可以通过以下事实解释：所有游戏都包含大量只玩一次的玩家。不幸的是，这些数据点只允许构建负例，从而可能导致类别分布的偏差。查看方法 M2 生成的数据集的统计数据，第一行显示训练数据集的统计数据，第二行显示测试数据的统计数据。相比游戏 5，游戏 1-4 的类别不平衡相当大。总体而言，游戏 5 的保留率更高（特别是第一天的保留率更高）。

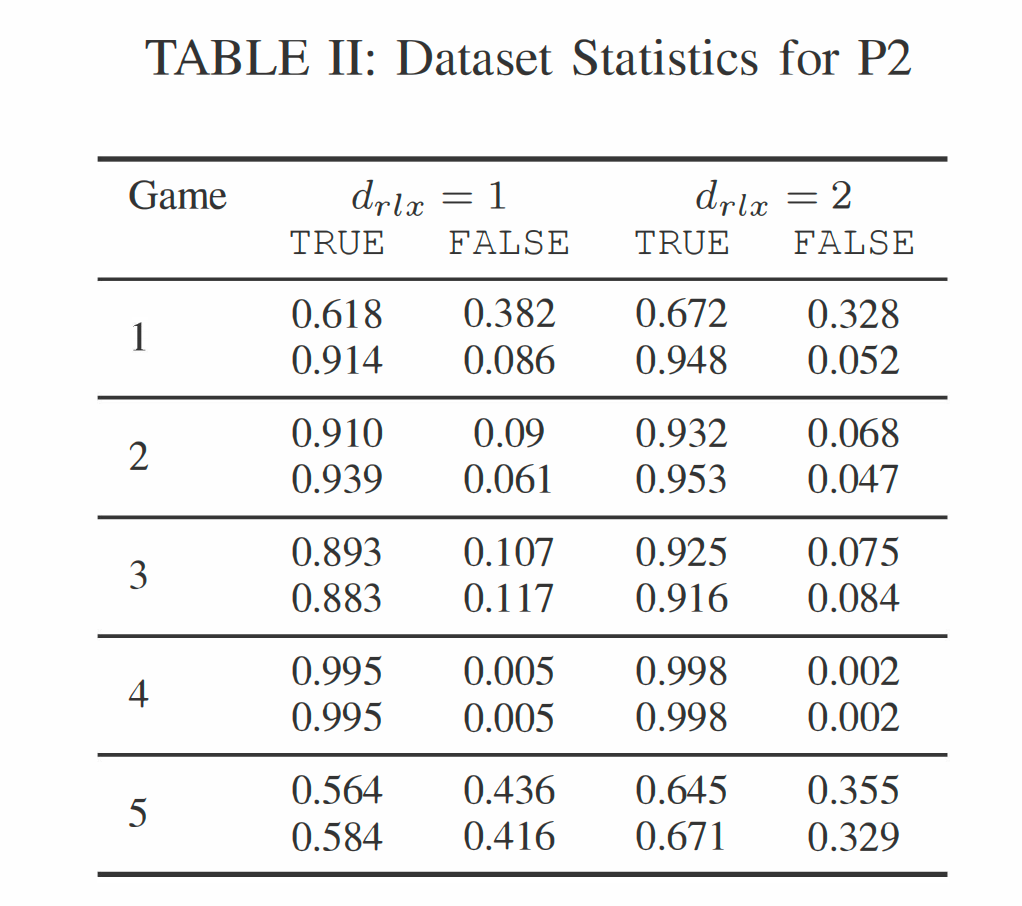
由于 M2 在现实环境中更具适用性，因此被认为是更重要的数据生成方法，我们仅使用方法 M2 评估 P2（初步结果也显示其行为/性能与 P1 相似）。相反，我们修改了新引入的滑动窗口大小参数。两个数据集在选择滑动时间窗口 $dr/x$ 上有所不同。对于第一个数据集，我们设置 $dr1x=1$，对于第二个数据集，我们设置 $dr1x=2$。我们观察到与 P1 数据集相似的统计数据，唯一的例外是 TRUE 类在游戏 5 中特别占主导地位。此外，请注意，随着窗口大小的增加，TRUE 类变得越来越占主导地位，最终，所有玩家都流失了。

IV. 特征

成功预测流失的最重要步骤之一是正确选择能够捕捉玩家行为并允许预测玩家流失的特征。由于我们正在构建一个与游戏内容无关的流失预测模型，我们提取了一组在我们平台上的所有游戏中通用的特征。在本节中，我们解释了我们在模型中使用的特征以及它们与玩家流失行为的关系。在第五节中，我们通过评估每个游戏训练的分类器中不同特征的重要性来展示上述特征的相对影响。

从对流失行为有明显影响的基本时间特征开始，我们使用会话数，即玩家过去活跃参与的会话数。此外，我们使用天数，代表玩家注册游戏以来的天数。这些特征被认为是重要的，因为快速流失是F2P游戏中的常见特征。我们还观察到，在数据集中某些游戏中，有些玩家在第一天或第二天后就流失了，有些玩家在只有一两次游戏会话后就流失了。此外，对于数据生成方法M2，我们加入了当前缺席时间，表示自玩家最近一次活动以来的时间。

对于MMORPG，基于会话的时间信息已被证明在建模玩家离开方面是有用的 [13]。因此，对于会话级别的粒度，我们考虑每次会话的平均游戏时间和会话之间的平均时间，前者表示玩家的总游戏时间除以会话数，后者表示会话之间的平均时间，即会话间时间。

为了捕捉游戏时间，我们使用两个用户在游戏中花费时间的时间模型。我们通过为每个玩家的个体观察拟合幂律函数来建模会话中的游戏时间，遵循过去关于游戏时间对预测对游戏兴趣下降的影响的研究 [21]。在这项工作中，我们使用游戏时间模型参数，即基于玩家的幂律函数（拟合到过去的观察数据）的参数，来表示玩家到预测日的游戏时间历史。此外，为了增加对特定游戏平均兴趣损失的影响，我们加入了保留值。也就是说，基于游戏的平均玩家保留率（通过拟合函数）构建保留模型，我们通过各自的游戏天数获得基于玩家的保留值。

鉴于应用内购买对F2P游戏的重要性，我们还整合了4个虚拟经济相关特征：高级用户标志、预定义消费类别、购买次数和每次会话的平均消费。我们使用高级用户标志来表示特定玩家是否有过购买行为。为了对玩家的整体购买体验进行分类，我们将一组预定义的消费类别输入到我们的模型中。这些消费类别根据玩家的相对消费分为三组，第一组是顶级消费玩家，第二组是平均消费玩家，最后一组是轻度消费玩家。接下来是玩家进行的总购买次数。最后一个虚拟经济相关特征是每次会话的平均消费，我们认为这是另一个重要的购买频率指标，我们测量每次游戏会话的平均消费金额。

V. 实验

在本节中，我们介绍了所提出的流失预测方法的实验评估。评估考虑了问题定义 PI 和 P2，以及应用于五款游戏的两种数据生成方法 MI 和 M2。综合起来，所使用的数据集涵盖了数十万名玩家，涉及数百万次会话。有关数据生成和数据集统计的详细信息，请参见第三节。对于 MI，所有数据集和组合都基于 10 折交叉验证方案进行评估。

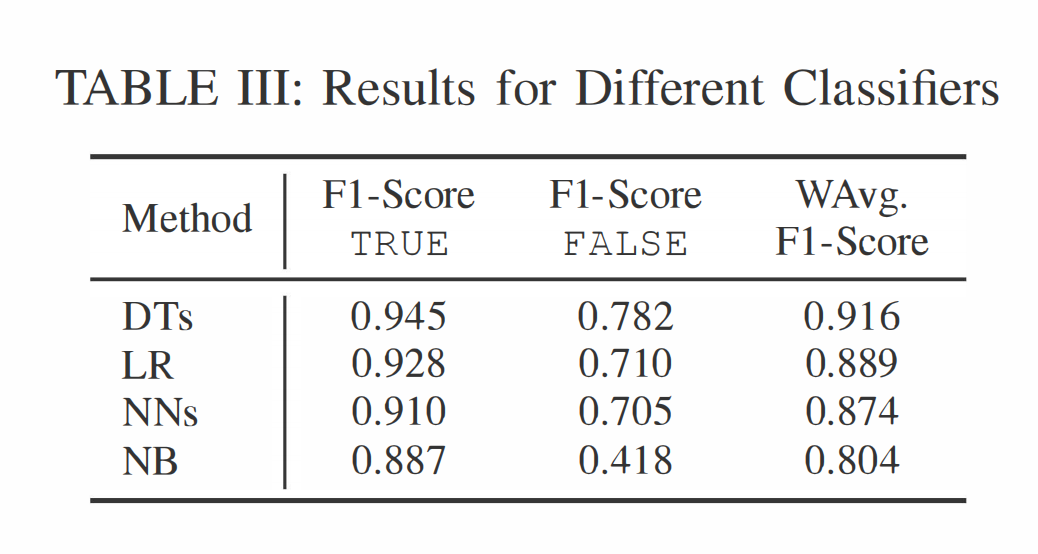
为了预测玩家流失，我们比较了多种不同的分类器，包括神经网络 (NNs)、逻辑回归 (LR)、朴素贝叶斯 (NB) 和决策树 (DTs)。由于对分类器的深入比较超出了本工作的范围，我们这里只报告关键结果。正如表 III 所示，我们发现决策树 [24] 在加权平均 F1 分数方面表现最好（总体上）在我们的一款游戏中。因此，在本节的其余部分，我们仅展示决策树的结果。决策树的一个具体优势是它们提供了相对简单和直观的解释手段，有助于描述流失预测中最重要和最具影响力的特征。

五款游戏的保留曲线显示出显著的流失率，但需要注意的是，游戏 4 的玩家流失率非常高，回归玩家的数量最少。因此，对于分类任务，拥有少数类可能会导致该特定类的预测不佳，而整体预测准确率仍然很高。通过使用 F 分数，我们试图缓解这些影响并使类不平衡更加明显。

A. PI 的结果

在表 IV 中，我们展示了针对玩家流失定义 PI 进行的实验结果。对于每款游戏，上行显示加权平均 F1 分数，下行显示流失玩家和非流失玩家的个体 F1 分数。对于 MI，加权 F1 分数接近 0.60，可以看出对非流失用户的分类准确性较差，可能是由于数据集不平衡，从而正例学习样本较少。与其他游戏相比，游戏 4 的整体表现出奇地好。然而，仔细查看个体分数，可以看到分类器在非流失玩家上完全失败。对于这款游戏，回归用户群体可以忽略不计，决策树学习器未能找到该类的良好模型。

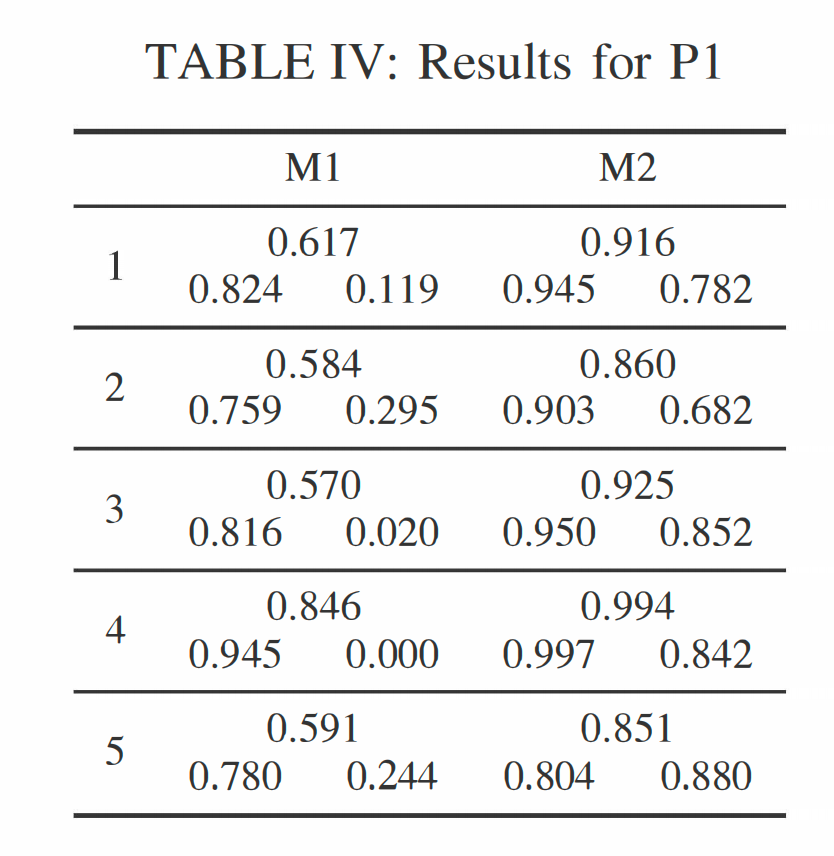
对于 M2，结果看起来有所不同。正如表 IV 右列所示，F1 分数相当高，非流失类的分数也高得多。总体而言，这些 F1 分数接近或超过文献中的结果，然而，由于使用了不同的游戏和行为特征，很难直接与相关工作进行比较。还需注意，这里考虑的游戏是 F2P/免费增值游戏，可以认为比相关工作中使用的主要商业 MMOG 更“休闲”。

看到由于不太受欢迎的游戏导致的类不平衡会导致较差的分类准确性，我们对在其他游戏和游戏类型中重现这里呈现的结果的能力充满信心。除了 MI 的游戏 4，特定数据生成方法的所有游戏分类性能相似。分数的观察到的差异是由于在所有游戏中，用户行为通过给定特征的手段捕捉得不一样好。总体而言，对于数据生成方法 M2，分类性能更高，尤其是对两类都更稳定。如前所述，M2 能够使用额外的特征“当前缺席时间”。正如我们将在下面对特征的更详细讨论中看到的，这个特定特征是预测玩家流失的最重要特征之一。

B. P2 的结果

在表 V 中，我们展示了结合数据生成方法 M2 进行的玩家流失定义 P2 的实验结果。我们这里只展示 M2 的结果，因为正如我们在上一节中所见，M2 比 MI 返回了更好的结果。在这里，我们改变了窗口大小 $drlx$。与之前的 M2 实验结果类似，总体 F1 分数很高，有趣的是，两个窗口大小的组合（加权平均）F1 分数相似。然而，随着窗口大小 $drlx$ 增加，FALSE 类的预测往往略有下降，因为类不平衡变得更严重。这再次表明，随着该组的消失，分类器找到回归玩家变得更加困难。

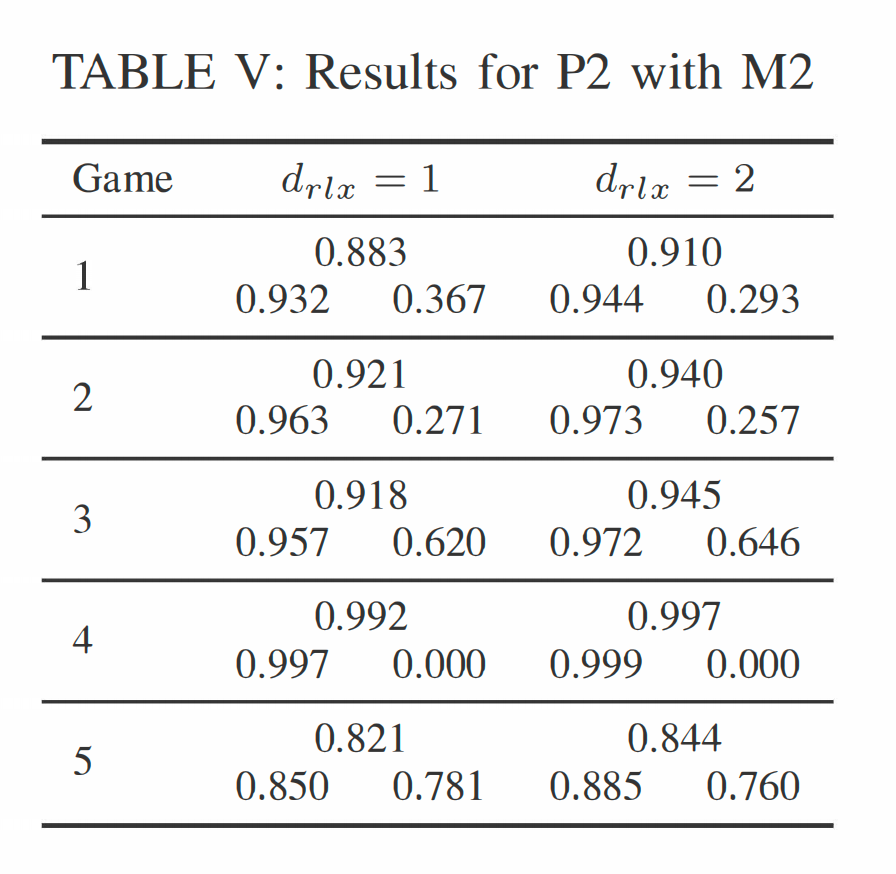
例如，对于游戏 4，即使在 $drlx=1$ 的情况下，非流失者的数量也是可以忽略的。非常重要的是，结果表明，在实际应用中，$drlx$ 的选择至关重要，其值需要根据各自游戏的平均用户参与度进行调整。显然，游戏 5 显示了最佳保留率，$drlx$ 的调整缓慢改变了玩家的分布。在两天的时间窗口内，非流失者的数量仍然足够大，开发者可以考虑影响这些玩家流失行为的方法。

参数 $drlx$ 提供了一种简单直观的方式，将一般的数据生成过程 M2 适应每个游戏的需求。实验表明，它确实对分类准确性有一定影响，并且允许根据不同的游戏或游戏类型定制分类器系统。因此，一旦特定游戏的额外（或历史）数据可用，使用所提出的分类器系统进行流失预测仍有优化的空间（但不是必要的）。

从实验中我们可以看到，对于某些游戏，预测玩家流失的问题可能是错误的。特别是，如果绝大多数玩家仅在一两次游戏会话后流失，预测玩家流失的任务似乎变成了一个随机过程，在这个过程中很难建立关于玩家为什么离开游戏的规则（例如考虑游戏 4）。对于大多数其他情况，所提出的分类器系统导致高准确性的玩家流失预测，这与实际游戏内容或游戏类型无关，因为所使用的特征是通用的。

C. 特征重要性

知道玩家即将离开游戏本身是有用的。然而，超越纯粹的流失预测，了解玩家即将离开的原因更为有用，因为它允许开发者尝试不同的行动并激励用户留下。显然，玩家可能停止玩特定游戏的原因是无限的或接近无限的。我们无法捕捉所有这些原因，但我们可以分析我们引入的特征中哪些特征在信息增益和分类器准确性方面最重要。

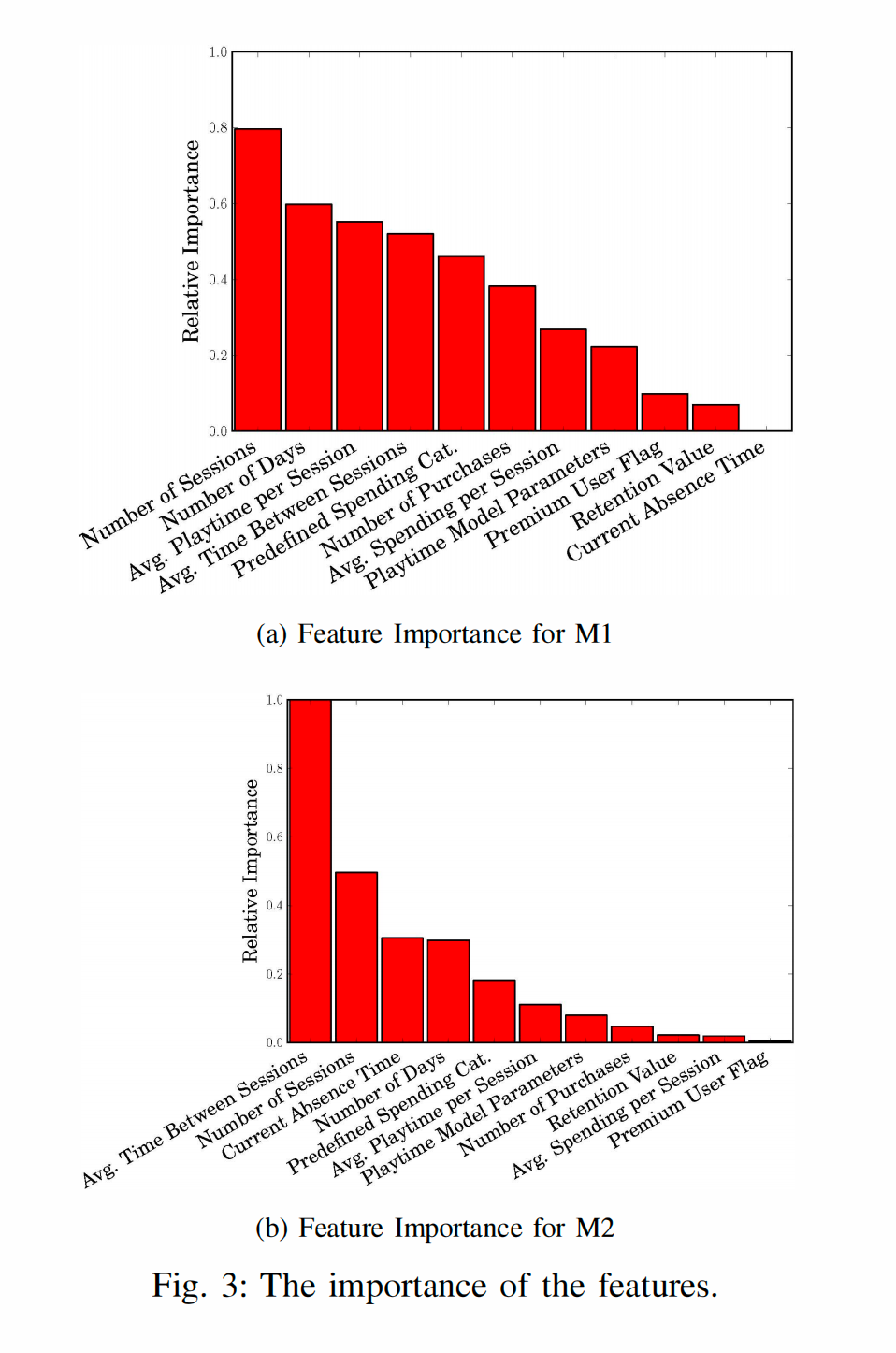
为了分析行为特征的相对重要性，我们仔细检查了学习到的决策树。在第一步中，我们统计了每个决策树使用每个特征的频率。对于 MI，特征“会话数”和“天数”最常出现。事实上，这两个特征是所有游戏中最决定性的特征。MI 中每个特征的相对重要性的全貌如图 3a 所示。有趣的是，所有树的根节点都是相同的，并且基于特征“天数”进行分支。除了这两个特征外，“会话之间的平均时间”也经常出现，除了游戏 1。这与 [13] 报告的结果一致，其中显示最终的会话间时间显著长于早期的会话间时间。因此，会话之间时间的增加表明玩家失去了兴趣，这被学习到的决策树规则捕捉到了。然而，我们的结果甚至超越了 Feng 等人的结果，因为我们报告了各种游戏的这些发现。

对于 M2，我们观察到特征重要性的变化（详见图 3b）。有趣的是，“会话之间的平均时间”现在成为最重要的特征，并出现在每个决策树中。这进一步强调了与 Feng 等人的发现的联系，如 MI 的情况所讨论的那样。从技术上讲，“会话之间的平均时间”通常是每个学习到的树的根节点，这进一步支持了其重要性。此外，我们现在可以观察到“当前缺席时间”始终在前五个特征中。这也部分解释了基于 M2 学习到的树的预测更稳定的原因。M2 随时间适应，因此更多地关注当前的用户群体，并且由于其访问实时特征（如“当前缺席时间”），分类准确性在类不平衡问题上更为稳定。

VI. 结论与未来工作

预测分析已成为商业智能的重要组成部分，也是数据驱动企业的核心需求。这在游戏开发中也是如此，随着“免费增值”商业模式或混合零售-免费增值模式的日益普及，分析游戏玩家的行为以了解他们的行为、改进设计和优化盈利变得越来越重要。与所有基于订阅的系统一样，对于游戏来说，采取措施留住客户通常比获得新客户更便宜，这使得流失预测对于通过游戏内购买和游戏内广告产生收入的 F2P 游戏非常重要 [2], [3], [6], [21], [25]。

在本文中，我们解决了预测免费增值游戏中玩家流失的挑战，提出了一种可以在现实条件下（即在实际环境中）应用于各种游戏的机器学习方法。该方法使用五款商业游戏的数据进行了测试，这些游戏分布在移动和基于 Web 的社交在线平台上。据作者所知，本研究与 [9] 一起，是第一个在多个游戏中进行 F2P 游戏流失预测的研究，并且仅使用与游戏无关的行为特征（如游戏时间和会话时间）。这是第一次在多个游戏中进行流失预测，也是第一次正式定义了游戏中的流失。我们总结如下贡献：

• 通过专门分析数字游戏的流失预测问题，我们正式引入了两种数据提取方法，以分析和提供游戏中流失行为的预测模型。第一种数据提取方法 MI 基于仅分析流失玩家，通过选择玩家的随机截止点创建负面示例。相比之下，通过将过去的任意时间设为截止点，我们定义了一种更适合现实世界环境的数据提取方法 M2，它使用所有玩家信息（即流失和非流失玩家）。

• 同样，定义了两种预测流失的正式模型，这取决于我们是在检测特定截止点的流失玩家还是在时间范围内的流失玩家（“硬” vs. “放松”流失窗口）。在第一个问题定义 PI 中，如果玩家在特定日期后没有返回，我们就检测到他们。在第二个问题定义中，提出了一种放松的定义 P2，我们在任意时间窗口内分析流失玩家，这种方法灵活，可以根据游戏的具体要求进行调整。具体来说，我们预测玩家是否会在截止日期后的某个时间内返回游戏。

• 我们不是基于游戏特定特征构建预测模型，而是提出了可以用于预测游戏中流失的通用基本和复合 F2P/免费增值行为特征，例如游戏时间、会话时间和会话间时间。

• 最后，我们在五款不同的商业 F2P 游戏（在线/移动）中，对不同的采样和流失定义组合使用不同的预测分类器（例如决策树、朴素贝叶斯），使用决策树获得了高准确率的分数。此外，我们展示了在确定游戏中的流失和非流失玩家时哪些行为特征是重要的，以及这些特征的重要性如何依赖于所分析的游戏。

鉴于游戏分析领域和游戏中行为预测领域的年轻化，有许多潜在的后续工作领域。简而言之，我们计划扩展所提出的模型，包括一种自适应方法来确定放松流失窗口（或软流失窗口）的长度，该方法由行为遥测信息提供，以便窗口长度是游戏特定的，甚至是类型特定的。我们还将使用不同的截止日期进行 M2，并寻求结合不同日期的分类器。此外，我们旨在研究跨游戏分析这一新兴领域，以利用类似游戏的数据对游戏进行推断。即，我们将研究免费增值游戏之间的相似性度量，以便对刚刚发布且没有足够用户进行预测分析的游戏进行早期预测。最后，在这里基于完整树构建预测模型之后，我们还计划研究当我们基于剪枝树构建模型时，预测结果将如何表现。

VII. 致谢

我们感谢 GameAnalytics 提供的数据集。本文的工作是在由 Fraunhofer ICON 计划资助的 Fraunhofer 和南安普顿大学研究项目 SoFWIReD 内进行的。

REFERENCES

[1] EI-Nasr, M.S. and Drachen, A. and Canossa, A., Game Analytics:
Maximizing the Value of Player Data. Springer, 2013.

[2] T. Fields and B. Cotton, Social Game Design: Monetization Methods
and Mechanics. Morgan Kaufmann, 201l.

[3] w. Luton, Free-to-Play: Making Money From Games You Give Away.
New Riders, 2013.

[4] T. Mutanen, J. Ahola, and S. Nousiainen, “Customer Churn PredictionA Case Study in Retail Banking,” in Proc. of ECMUPKDD Workshop
on Practical Data Mining, 2006, pp. 13-19.

[5] “The playtime principle: Large-scale cross-games interest modeling,” in
Proc. IEEE CIG, 2014.

[6] A. Drachen, C. Thurau, J. Togelius, G. Yannakakis, and C. Bauckhage,
“Game Data Mining,” in Game Analytics: Maximizing the Value of
Player Data, M. EI-Nasr, A. Drachen, and A. Can ossa, Eds. Springer,
2013.

[7] M. Mozer, R. Wolniewicz, D. Grimes, E. Johnson, and H. Kaushansky,
“Predicting Subscriber Dissatisfaction and Improving Retention in the
Wireless Telecommunications Industry,” IEEE Trans. on Neural Networks, vol. 11, no. 3, pp. 690-696, 2000.

[8] G. Dror, D. Pelleg, O. Rokhlenko, and I. Szpektor, “Churn Prediction
in New Users of Yahoo! Answers,” in Proc. of the 21st international
conference companion on World Wide Web, 2012.

[9] “Churn prediction for high-value players in casual social games,” in
Proc. IEEE CIG, 2014.

[10] G. Yannakakis, “Game AI Revisited,” in Proc. of ACM Computing
Frontiers Conference, 2012, pp. 285-292.

[11] C. Thurau, T. Paczian, and C. Bauckhage, “Is Bayesian Imitation
Learning the Route to Believable Gamebots?” in Proc. GAME-ON NA,
2005.

[12] R. Sifa and C. Bauckhage, “Archetypical Motion: Supervised Behavior
Learning Using Archetypal Analysis,” in Proc. IEEE CIG, 2013.

[13] W. Feng, D. Brandt, and D. Saha, “A Long-term Study of a Popular
MMORPG,” in Proc. of the 6th ACM SIGCOMM Workshop on Network
and System Support for Games, 2007.

[14] C. Chambers, W. Feng, S. Sahu, and D. Saha, “Measurement-based
Characterization of a Collection of On-line Games,” in Proc. of ACM
SIGCOMM Conf. on Internet Measurement, 2005.

[15] Z. Borbora, J. Srivastava, K.-w. Hsu, and D. Williams, “Churn Prediction in MMORPGS Using Player Motivation Theories and an Ensemble
Approach,” in Proc. of IEEE International Coriference on Social Computing, 2011, pp. 157-164.

[16] J. Kawale, A. Pal, and J. Srivastava, “Churn Prediction in MMORPGs:
A Social Influence Based Approach,” in Proc. of the 2009 International
Conference on Computational Science and Engineering, 2009.

[17] K. Morik and H. Kopcke, “Analysing Customer Churn in Insurance
Data-A Case Study,” in PKDD, 2004, pp. 325-336.

[18] J. Ferreira, M. Vellasco, M. Pacheco, R. Carlos, and H. Barbosa,
“Data Mining Techniques on the Evaluation of Wireless Churn,” in
Proc. of European Sym. on Artificial Neural Networks, Computational
Intelligence and Machine Learning, 2004, pp. 483-488.

[19] H. Hwang, T. Jung, and E. Suh, “An LTV Model and Customer
Segmentation Based on Customer Value: A Case Study on the Wireless
Telecommunication Industry,” Expert systems with applications, vol. 26,
no. 2, pp. 181-188, 2004.

[20] S. Yoon, J. Koehler, and A. Ghobarah, “Prediction of Advertiser Churn
for Google Adwords,” in Proc. of JSM, 2010.

[21] C. Bauckhage, K. Kersting, R. Sifa, C. Thurau, A. Drachen, and
A. Canossa, “How Players Lose Interest in Playing a Game: An
Empirical Study Based on Distributions of Total Playing Times,” in
Proc. IEEE CIG, 2012.

[22] B. Weber, M. John, M. Mateas, and A. Jhala, “Modeling Player
Retention in Madden NFL 11,” in IAAl, 201l.

[23] D. Pittman and C. GauthierDickey, “Characterizing Virtual Populations
in Massively Multiplayer Oline Role-playing Games,” in Proc. of the
16th Int. Conf. on Advances in Multimedia Modeling, 2010, pp. 87-97.

[24] R. Quinlan, C4.5: Programs for Machine Learning. San Mateo, CA:
Morgan Kaufmann Publishers, 1993.

[25] E. B. Seufert, Freemium Economics: Leveraging Analytics and User
Segmentation to Drive Revenue. Elsevier, 2014.