课程作业原地址:CS231n Assignment 1
作业及整理:@林凡莉 && @Molly && @寒小阳
时间:2018年1月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/79139395
1 任务
在这个练习里,我们将实现一个完全连接的神经网络分类器,然后用CIFAR-10数据集进行测试。
2 知识点
2.1 神经元
要讲神经网络就得先从神经元开始说起,神经元是神经网络的基本单位,它的结构如下图所示:
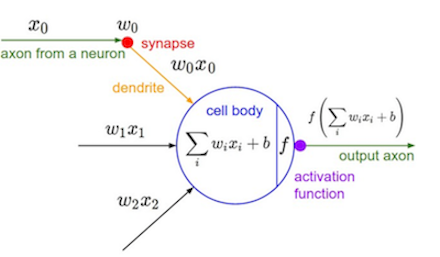
神经元不管它的名字有多逼格,它本质上不过是一个函数。就像每个函数都有输入和输出一样,神经元的输入是一个向量,里面包含了很多个 xi (图左边),输出的是一个值(图右边)。神经元在这个过程中只做了两件事:一是对输入向量做一次仿射变换(线性变化+平移, scaling+shift),用公式表示就是
∑iwixi+b
二是对仿射变换的结果做一次非线性变换,即
f(∑iwixi+b)
这里的f就叫做激活函数。权值
wi
和偏置项
b
是神经元特有的属性,事实上,不同神经元之间的差别主要就三点:权重值,偏置项,激活函数。总的来说,神经元的工作就是把所有的输入项
激活函数有很多种,下面介绍一个叫sigmoid的激活函数:
这个函数很有意思,它把任何一个属于值域R的实数转换成0到1之间的数,这使得概率的诠释变得可能。但是在训练神经网络的时候,它有两个问题,一是当输入的仿射变换值太大或者太小的时候,那f关于x的梯度值就为0,这不利于后面提到的反向传播算法中梯度的计算。第二个问题在于它的值不是中心对称的,这也导致梯度更新过程中的不稳定。Sigmoid的函数图像大概长下面这样:
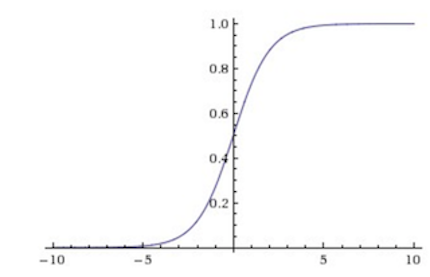
如果现在我们把实数1也放进输入的向量中得到 x⃗ ,把偏置项放进权值向量中得到 w⃗ ,那么包含sigmoid激活函数神经元的工作就可以简洁地表示为:
y=sigmoid(w⃗








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 2088
2088











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








