巴特沃斯数字低通滤波器的设计步骤

Hello，欢迎来到我的博客~~~

1 低通滤波器性能指标

低通滤波器的主要性能指标有四个：

1. 通带截止频率：通带内幅值下降至一定程度时对应的频率，单位为：Hz或角频率
2. 阻带截止频率：阻带内幅值高于一定程度时对应的频率，单位为：Hz或角频率
3. 通带纹波（衰减）：通带中最大幅值和最小幅值之间的差值，单位为：dB
4. 阻带衰减：阻带中最大幅值和通带最大幅值的差值，单位为：dB

幅值单位：dB，计算方式：$20{\log }_{10}A$
示例：

1. 假如幅值响应是100，那么相当于$20{\log }_{10}100=40$ dB
2. 假如通带最大幅值是100，阻带最大幅值是10，那么阻带衰减就是$20{\log }_{10}10-20{\log }_{10}100=-20$ dB

2 巴特沃斯模拟低通滤波器设计步骤

2.1 巴特沃斯低通滤波器的传递函数

极点形式：
$$H(s)=G_0\prod _{k=1}^n\frac{1}{s-{\omega }_c{s}_k},s_k=\exp \frac{j(2k+n-1)}{2n},k=1,2,3,...,n$$
其中，${\omega }_c$就是-3dB截止频率，$n$是滤波器阶数，$G_0$是直流增益，一般取1。
多项式形式：
$$H(s)=\frac{G_0}{{\sum }_{k=0}^n{a}_k(s/{\omega }_c{)}^k},a_k=\prod _{\mu =1}^k\frac{\cos ((\mu -1)\gamma )}{\sin (\mu \gamma )},a_0=1,\gamma =\frac{\pi }{2n},k=1,2,3,...,n$$
对应于不同阶数的滤波器，$s_k$和$a_k$的值都是可以事先计算好，然后查表得到的，如下示例：

2.2 频率响应

根据巴特沃斯滤波器的传递函数，可以推得其频率响应为：
$$|H(j\omega ){|}^2=\frac{G_0^2}{1+(\frac{\omega }{{\omega }_c}{)}^{2n}}$$

根据上述的频率响应，很容易分析得到当$\omega$趋于0时，频率响应趋于$G_0^2$，当$\omega$趋于无穷时，频率响应趋于0。

2.3 设计步骤

1. 给定通带截止频率${\omega }_p$，阻带截止频率${\omega }_s$，通带纹波${\alpha }_s$和阻带衰减${\alpha }_p$，计算滤波器阶数N

计算两个辅助变量：$k_{sp}=\sqrt{\frac{10^{0.1{\alpha }_s}-1}{10^{0.1{\alpha }_p}-1}}$, ${\lambda }_{sp}=\frac{{\omega }_s}{{\omega }_p}$

计算阶数（向上取整）：$N=\frac{\lg k_{s}p}{\lg {\lambda }_{sp}}$

2. 根据滤波器阶数，通过查表得到滤波器传递函数的系数

如上文所示，从表格中找出对应阶数滤波器的系数值：$a_k$
3. 计算3 dB截止频率${\omega }_c$
${\omega }_c={\omega }_p(10^{0.1a_p}-1{)}^{-\frac{1}{2N}}$

4. 代入系数和${\omega }_c$，得到最终的滤波器传递函数

$H(s)=\frac{G_0}{{\sum }_{k=0}^n{a}_k(s/{\omega }_c{)}^k}$

3 巴特沃斯数字低通滤波器设计步骤（IIR实现）

1. 选择一个归一化的模拟滤波器（确定巴特沃斯低通滤波器的阶数）
2. 确定数字滤波器的3 dB截止频率
3. 利用公式计算模拟滤波器的3 dB截止频率

$f_a=\frac{f_s}{\pi }\tan \frac{\pi f_d}{f_s}$
$f_s$是采样频率，$f_d$是数字滤波器截止频率

4. 将模拟截止频率${\omega }_c=2\pi f_a$带入模拟滤波器传递函数$H(s)$
5. 用双线性变换，把模拟滤波器传递函数中的$s$替换为$z$，得到$H(z)$

双线性变换：$s=2f_s(\frac{z-1}{z+1})$

4 巴特沃斯高通、带通、带阻数字滤波器的设计

要设计高通、带通、带阻等数字滤波器，有两种思路。

1. 低通模拟滤波器 =》=》高通、带通、带阻模拟滤波器 =》=》高通、带通、带阻数字滤波器
2. 低通模拟滤波器 =》=》高通、带通、带阻数字滤波器

这里主要介绍的是第二种思想，方法如下图所示：

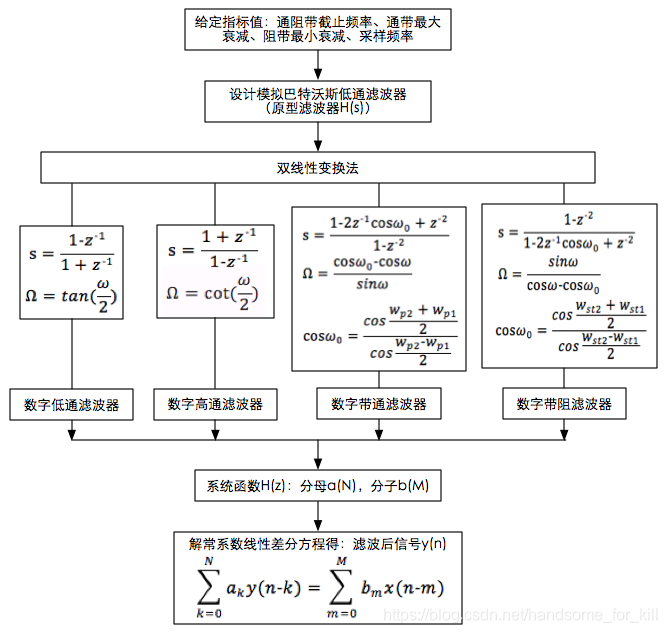
4.1 变量说明

• $\omega =\frac{2\pi f_p}{f_s}$，其中，$f_p$是数字通带截止频率
• $\Omega =\frac{2\pi F_p}{f_s}$，其中，$F_p$是模拟通带截止频率（注意这里的符号和上文有差异，不要混淆）
• ${\omega }_{p1}=\frac{2\pi f_{p1}}{f_s}$，其中，$f_{p1}$是数字下通带截止频率（带通滤波器）
• ${\omega }_{p2}=\frac{2\pi f_{p2}}{f_s}$，其中，$f_{p2}$是数字上通带截止频率（带通滤波器）
• ${\omega }_{st1}=\frac{2\pi f_{st1}}{f_s}$，其中，$f_{st1}$是数字下阻带截止频率（带阻滤波器）
• ${\omega }_{st2}=\frac{2\pi f_{st2}}{f_s}$，其中，$f_{st2}$是数字上阻带截止频率（带阻滤波器）

4.2 设计步骤

根据上图，设计步骤可以描述如下：

1. 选定巴特沃斯滤波器的阶数，可以得到一个归一化的巴特沃斯低通滤波器，形式如下：
   $$H(p)=\frac{1}{{\sum }_{k=0}^N{a}_k{p}^k}$$

2. 针对不同的滤波器形式，利用图中公式计算出$\Omega$，并在$H(p)$中带入$p=\frac{s}{\Omega }$，得到$H(s)$

3. 针对不同的滤波器形式，利用图中公式，将$H(s)$公式中的$s$用$z$变量替换，得到$H(z)$

注意事项：
上图中对应低通、高通、带通、带阻都有$s$和$\Omega$的计算方法
需要注意的是，
对于低通和高通而言，$\omega$一般指的都是通带$3$ dB截止频率
对于带通和带阻而言，$\omega$一般指的都是上通带或上阻带$3$ dB截止频率

4.3 设计示例

4.3.1 巴特沃斯数字高通滤波器

给定条件：滤波器阶数为1，数字滤波器通带截止频率为30 Hz，采样频率为100 Hz
第一步：查表，得到归一化巴特沃斯低通滤波器形式：
$$H(p)=\frac{1}{p+1}$$
第二步：计算$\omega$和$\Omega$，在$H(p)$中带入$p=\frac{s}{\Omega }$
$$\omega =\frac{2\pi \ast 30}{100}=0.6\pi ,\Omega =\cot \frac{\omega }{2}=0.7265$$
$$H(s)=\frac{0.7265}{s+0.7265}$$
第三步：将$H(s)$公式中的$s$用$z$变量替换
$$H(z)=\frac{0.7265}{\frac{z-1}{z+1}+0.7265}=\frac{0.7265z-0.7265}{1.7265z+0.2735}=\frac{0.4208z-0.4208}{z+0.1584}$$
以上是设计得到的巴特沃斯数字高通滤波器，利用Matlab可以验算结果，和公式计算的完全一致。

Matlab命令：
fc = 30; fs = 100; [a,b]=butter(1, fc/(fs/2), ‘high’)
结果：
a = [0.4208, -0.4208] % 分子多项式系数
b = [1.0000, 0.1584] % 分母多项式系数

4.3.2 巴特沃斯数字带阻滤波器

给定条件：滤波器阶数为2，数字滤波器上阻带截止频率为15 Hz，下阻带截止频率为10 Hz，采样频率为100 Hz
第一步：查表，得到归一化巴特沃斯低通滤波器形式：
$$H(p)=\frac{1}{p^2+1.4142p+1}$$
第二步：计算$\omega$，${\omega }_{st1}$，${\omega }_{st2}$和$\Omega$，在$H(p)$中带入$p=\frac{s}{\Omega }$
$$\begin{array}{rl}& {\omega }_{st1}=\frac{2\pi \ast 10}{100}=0.2\pi ,{\omega }_{st2}=\frac{2\pi \ast 15}{100}=0.3\pi ,\\ & \cos {\omega }_0=\frac{\cos \frac{{\omega }_{st2}+{\omega }_{st1}}{2}}{\cos \frac{{\omega }_{st2}-{\omega }_{st1}}{2}}=\frac{\cos \frac{0.3\pi +0.2\pi }{2}}{\cos \frac{0.3\pi -0.2\pi }{2}}=0.7159,\\ & {\Omega }_{st1}=\frac{\sin {\omega }_{st1}}{\cos {\omega }_{st1}-\cos {\omega }_0}=\frac{\sin 0.2\pi }{\cos 0.2\pi -0.7159}=6.3123,\\ & {\Omega }_{st2}=\frac{\sin {\omega }_{st2}}{\cos {\omega }_{st2}-\cos {\omega }_0}=\frac{\sin 0.3\pi }{\cos 0.3\pi -0.7159}=-6.3148,\\ & \Omega ={\Omega }_{st1}\end{array}$$
$$H(s)=\frac{6.3123^2}{s^2+6.3123s+6.3123^2}=\frac{39.8451}{s^2+6.3123s+39.8451}$$
第三步：将$H(s)$公式中的$s$用$z$变量替换
$$\begin{array}{rl}H(z)& =\frac{39.8451}{(\frac{z^2-1}{z^2-2\cos {\omega }_{0}z+1}{)}^2+6.3123\frac{z^2-1}{z^2-2\cos {\omega }_{0}z+1}+39.8451}\\ & =\frac{39.8451(z^2-1.4318z+1{)}^2}{(z^2-1{)}^2+6.3123(z^2-1)(z^2-1.4318z+1)+39.8451(z^2-1.4318z+1{)}^2}\\ & =\frac{39.8451(z^4-2.8636z^3+4.0501z^2-2.8636z+1)}{47.1574z^4-123.1384z^3+159.3747z^2-105.0625z+34.5328}\\ & =\frac{0.8449z^4-2.4196z^3+3.4221z^2-2.4196z+0.8449}{z^4-2.6112z^3+3.3796z^2-2.2279z+0.7323}\end{array}$$
以上是设计得到的巴特沃斯数字高通滤波器，利用Matlab可以验算结果，和公式计算的基本一致。

Matlab命令：
fst1 = 10; fst2 = 15; fs = 100; [a,b]=butter(2,[fst1/(fs/2),fst2/(fs/2)],‘stop’)
结果：
a = [0.8006, -2.2926, 3.2425, -2.2926, 0.8006] % 分子多项式系数
b = [1.0000, -2.5494, 3.2024, -2.0359, 0.6414] % 分母多项式系数

5 参考资料

参考链接：从模拟滤波器到数字滤波器
数字信号处理公式变程序（四）——巴特沃斯滤波器（上）
数字信号处理教程（超浓缩版）