用于机载STAR-RIS辅助通信的双Actor DDPG算法

大家读完聚德有帮助记得关注和点赞！！！

摘要​

本研究摒弃了当前机载同时透射反射可重构智能表面（STAR-RIS）研究中普遍假设的透射和反射系数（TRC）相互独立的做法。相反，我们探索了一种新颖的多用户下行链路通信系统，该系统利用搭载在无人机（UAV）上的STAR-RIS（空中STAR，Aerial-STAR），并采用了一种耦合的TRC相移模型。我们的主要贡献包括联合优化无人机轨迹、基站的主动波束成形向量以及无源RIS的TRC，以在考虑无人机能量约束的同时提升通信效率。我们将TRC设计为离散和连续动作的组合，并提出了一种新颖的双Actor深度确定性策略梯度（DA-DDPG）算法。该算法依赖两个独立的Actor网络来处理高维混合动作空间。我们还提出了一种基于新颖调和平均指数（HFI）的奖励函数，以确保用户间的通信公平性。为了进行全面分析，我们研究了RIS尺寸对无人机空气动力学的影响，表明它会增加阻力和能量需求。仿真结果表明，所提出的DA-DDPG算法在累积奖励方面分别优于传统的DDPG和基于DQN的解决方案24%和97%。三维无人机轨迹优化相比二维和高度优化实现了28%的通信效率提升。基于HFI的奖励函数相比其他基准提供了41%更低的QoS拒绝率。移动的Aerial-STAR系统显示出优于固定部署对应方案的性能，其中耦合相位的STAR-RIS优于双透射/反射RIS（T/R-RIS）和传统RIS设置。这些发现突显了Aerial-STAR系统的潜力以及我们提出的DA-DDPG方法在优化其性能方面的有效性。

关键词​

6G网络，同时透射反射RIS，无人机，双Actor，强化学习

​1 引言​

在追求超越5G（B5G）和第六代（6G）网络的下一代进展过程中，对高频谱效率、高能效、超低延迟和广泛覆盖的迫切需求是主要驱动力[1]。作为这些需求的衍生技术，可重构智能表面（RIS）以及无人机在无线网络中日益增多的应用，已成为塑造无线通信未来格局的前沿技术[2]。可重构智能表面（RISs）是由能够动态改变电磁波相位的无源元件组成的创新结构。这些表面充当“智能镜子”，可以操纵无线信号的传播环境。通过调整反射波的相位，RIS可以增强信号强度，减轻干扰，并在发射器和接收器之间建立有效的通信链路[3]。

虽然传统的RIS技术在增强无线通信方面显示出潜力，但其服务范围仅限于反射空间[4]。STAR-RIS通过实现同时透射和反射克服了这一限制，从而提供360°覆盖[5]并缓解了RIS朝向问题。STAR-RIS技术代表了无线通信系统的范式转变，与传统RIS相比具有优势，包括扩展的服务覆盖范围、增加的波束成形灵活性以及提供360°覆盖的能力[6]。这种变革潜力增强了在下一代无线网络中采用STAR-RIS解决方案的吸引力。

此外，STAR-RIS实现中采用的相移模型的选择显著影响系统性能。使用实用的耦合相移模型[7]而非独立相移模型会由于透射和反射系数的相互依赖性而降低性能，但被认为是两者中更现实的一个[7]，并提高了解决方案的可靠性。这种方法确保了STAR-RIS赋能网络的整体解决方案的可靠性。

尽管STAR-RIS具有优势，但其在固定位置部署时的有效性可能会受到限制，特别是在有移动用户或动态环境的场景中。通过将STAR-RIS安装在无人机上，我们可以将STAR-RIS技术的优势与无人机的机动性和促进视距（LoS）传输的能力相结合[8]。使用无人机进行空中通信可以促进高效的资源分配和网络优化[9]。这种Aerial-STAR方法允许RIS动态定位，潜在地改善视距条件并实时适应变化的用户分布。

搭载RIS的无人机系统在平衡通信性能与能量约束方面面临独特挑战。为了最大化通信效率，我们提出了一个联合优化框架，考虑Aerial-STAR轨迹、基站的主动波束成形向量和无源RIS TRC。据我们所知，这是首个在无人机通信中包含STAR-RIS实用相移模型的研究。该框架还考虑了无人机的能量限制以及STAR-RIS相关的空气动力学效应。

这项工作的主要贡献¹如下：

• 我们提出了一种新颖的双Actor深度确定性策略梯度（DA-DDPG）算法，该算法具有两个独立的Actor网络，旨在有效管理为STAR-RIS实现实用相移设计时出现的复杂动作空间。具体来说，DA-DDPG解决了Aerial-STAR所需的高维连续和离散动作组合所带来的挑战。

• 我们引入了一种新的公平性度量，称为调和公平指数（HFI）。基于调和平均数，HFI旨在通过允许更公平的资源分配来帮助所有用户达到最低数据速率。

• 仿真结果²表明，DA-DDPG算法表现出色，它为连续和离散动作提供了专业化处理，在累积奖励方面超越了传统的单Actor DDPG（24%）和DQN（97%）算法。基于DA-DDPG的Aerial-STAR相比传统RIS和双透射/反射（T/R）RIS提供了22%的效率提升。此外，Aerial-STAR的三维轨迹优化优于STAR RIS的固定部署和其他轨迹配置。在奖励函数中融入HFI被证明能在所比较的方法中提供最大的用户公平性。

​2 相关工作与动机​

​2.0.1 无人机使能的RIS通信​

无人机因其经济性、卓越的机动性和促进视距（LoS）传输的能力而在无线网络中得到广泛采用[10]。这些特性可以与STAR-RIS的能力相结合以提供更好的覆盖。[11]提出在无人机网络中的建筑物外墙上安装固定的STAR-RIS，通过优化无人机位置和STAR RIS TRC来最大化无人机-用户和速率。类似地，[12]联合优化波束成形向量、无人机轨迹和功率分配，以使用固定STAR-RIS最大化和速率。

尽管无人机为固定STAR-RIS的通信提供了一些增加的自由度，但这并不能缓解RIS与移动用户之间非视距（NLoS）信道高概率的问题。[13]中提出了搭载在无人机上的RIS的概念，表明移动RIS由于强LoS信道可以增强通信体验。在[14]中，证明了引入搭载在无人机上的RIS可以显著改善中断性能，无论该RIS是静止还是移动的。所有这些研究工作都集中在仅反射的RIS搭载在无人机上。这个概念最近扩展到无人机搭载的STAR-RIS[15]，该研究提出优化任务卸载、无人机轨迹、RIS TRC和发射功率以最大化能量效率（原文为consumption，但结合上下文，更可能是efficiency）。

然而，在这两种情况下，无论STAR-RIS是作为无人机网络中的地面辅助设备还是直接安装在无人机上，一个普遍的假设盛行——透射和反射的相移系数可以独立调整。这个假设暗示了在任意改变相应的电感和磁感阻抗方面具有不切实际的灵活性。这个假设可能不适用于无源STAR-RIS配置，因为其可行的电感和磁感阻抗仅限于纯虚数[16]，这构成了我们工作的动机。

​2.0.2 RIS辅助网络中的强化学习（RL）​​

最近的研究表明，RL能够智能地管理RIS和无人机轨迹[17, 18, 19]。[17]引入了一种DQN算法，旨在通过优化无人机轨迹和无源相移RIS系数来增强能量效率。类似地，[18]提出了一种双延迟DDPG（TD3）算法，通过联合优化RIS相移和波束成形向量来满足服务质量（QoS）约束。然而，这些方法存在仅提供180°覆盖的限制。另一方面，[19]和[20]使用STAR RIS实现360°覆盖，但利用了双DQN（Double-DQN）。DQN的缺点在于其无法输出适用于RIS相位和无人机轨迹设计的连续动作。考虑连续/混合动作空间的解决方案通常要么设置静态RIS[21]，要么设置独立相移[22]，这两者都遭受了先前讨论的局限性。

​2.0.3 针对离散/连续动作空间的基于RL的解决方案​

对于STAR RIS系统，优化透射和反射系数至关重要，其动作空间可以建模为连续和离散动作的组合（在第4节讨论）。一些工作研究了管理连续和离散动作空间。例如，[23]证明了多Actor集中式评论家框架可以有效地处理协调挑战，并提高在连续和离散动作空间中的学习稳定性。[24]证明了使用专门的输出分支处理离散和连续动作，在视频游戏AI中比传统的单输出方法能更好地处理混合动作空间。同样，[25]开发了一种混合Actor-Critic算法，具有专门的离散和连续动作输出，用于机器人控制任务，取得了优于依赖动作空间近似或专家启发式方法的结果。为了处理类似问题，[26]提出了动作分支架构，表明针对不同动作类型的独特网络分支增强了在混合动作空间中的性能。这些例子说明了使用专门架构组件优化STAR-RIS的潜在优势，突出了它们如何有效处理连续和离散动作，同时通过共享状态表示保持协调。

​2.0.4 动机​

对文献的分析揭示了现有研究工作中的几个局限性。虽然许多工作集中于使用传统的仅反射RIS[27, 14, 10]，其服务区域有限，仅限于反射空间，但一些工作通过采用STAR-RIS[28, 29]克服了这一限制。然而，它们通常假设存在预先安装的支持基础设施，而这可能并不总是可用。另一个挑战来自固定的RIS安装，它们可能并不总是与移动用户有视距（LoS）信道，尤其是在城市场景中。无人机搭载的STAR-RIS被提出来解决这些问题[22, 14]，但大多数研究假设任意的相位系数，这对于无源RIS来说是不切实际的。由于相互依赖性，STAR-RIS的耦合透射和反射波束成形的有效设计具有挑战性。这种复杂性需要一个允许集成连续和离散动作的控制方案——这是现有相关算法难以满足的要求，因为这些算法是为相对较小的动作空间设计的[24]，由于RIS涉及的大动作维度[21]。此外，通过专门的网络分别处理这些动作可能会带来改进的性能。考虑到现有研究的局限性和所涉及的挑战，我们提出了一种DA-DDPG算法，具有两个专门的Actor，每个Actor设计用于独立处理连续和离散动作。这种方法利用混合Actor-Critic方法的最新进展来解决高维动作空间。

​3 系统模型​

​3.1 系统描述​

我们考虑一个下行链路通信网络，包括一个位于 (x_b, y_b, z_b)^T 的 M 天线基站和一个位于 T_s = (x_s, y_s, z_s)^T 的具有 N 个元件的 Aerial-STAR，如图 1 所示。STAR-RIS 工作在能量分割（ES）模式，将每个元件入射信号的能量分割给透射和反射区域。在透射和反射区域分别有 𝒯 和 ℛ 个单天线用户。J 是用户总数，满足 J = P + Q，其中 P 和 Q 分别表示 ℛ 和 𝒯 用户的数量，它们位于 (x_j, y_j, z_j)^T。

β_n^ℛ 和 β_n^𝒯, n=1,2,…,N 分别代表每个元件对 ℛ 和 𝒯 用户的幅度响应。反射和透射相移表示为 θ_n^ℛ, θ_n^𝒯 ∈ (0,2π]。每个元件的 TRC 表示为 β_n^𝒯 e^{j θ_n^ℛ} 和 β_n^R e^{j θ_n^R}，并且需要为无源波束成形进行优化，这是非平凡的，因为每个元件的 TRC 由其阻抗控制。对于一个无源无耗 RIS [7]，能量守恒定律要求 β_n^ℛ = √(1 - (β_n^𝒯)²)。相移通过关系 cos(θ_n^ℛ - θ_n^𝒯) = 0 耦合，并遵循

一个 N 元件 STAR-RIS 的 TRC 矩阵 𝚽 表示为

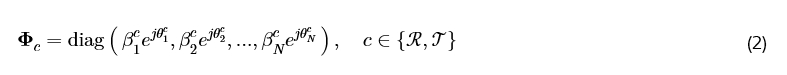
因此，基于 ES 的 STAR-RIS 可以为 ℛ 用户和 𝒯 用户支持 N 条多径。然而，如前所述，增强的多径增益优势是以配置 TRC 的灵活性有限为代价的，这些系数不能任意或独立地调整。

​3.2 信道和信号模型​

在我们的系统中，我们考虑需要精确建模的多个无线信道。这些包括 Aerial-STAR 和基站之间的信道 (H_bs ∈ ℂ^{M×N})，从 BS 到 ℛ (H_bℛ ∈ ℂ^{M×P})，BS 到 𝒯 用户 (H_b𝒯 ∈ ℂ^{M×Q}) 的信道，以及从 Aerial-STAR 到 ℛ (H_sℛ ∈ ℂ^{N×P}) 和 𝒯 用户 (H_s𝒯 ∈ ℂ^{N×Q}) 的信道。这里 N 是 Aerial-STAR 中的元件数量，M 是 BS 天线数量，P 是反射用户数量，Q 是透射用户数量。对于每个特定用户，这些信道可以表示为 h_bu ∈ ℂ^{M×1}, h_su ∈ ℂ^{N×1}，其中 u ∈ p,q。

所有信道都使用准静态块衰落方法建模，其中衰落系数在每个时隙 (t) 内保持恒定，但可能根据 Aerial-STAR、基站和用户的当前位置从一个时隙变化到下一个时隙。Aerial-STAR 和 BS 之间的信道 H_bs 被建模为莱斯衰落信道，同时考虑视距（LoS）和非视距（NLoS）分量：

​

​图 1: Aerial-STAR 辅助网络的系统模型。​​

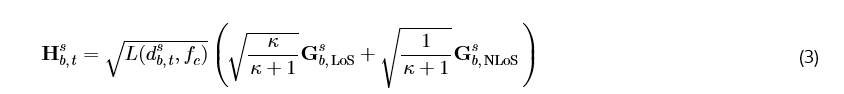
其中 L(d{b,t}^s, f_c) 表示路径损耗，κ 是莱斯因子，G{b,NLoS}^s ∈ ℂ^{N×M} ∼ 𝒞𝒩(0,1) 表示散射路径带来的增益，G_{b,LoS}^s ∈ ℂ^{N×M} 是 STAR-RIS 和 BS 之间的 LoS 链路。其定义为

其中 a_b ∈ ℂ^{M×1} 和 a_s ∈ ℂ^{N×1} 分别是 BS 和 Aerial-STAR 的天线阵列响应向量。θ, ϕ, 和 ψ 表示到达/离开的方位角和仰角[30]。根据[19]，对于 BS 的线性阵列和 STAR-RIS 的均匀平面阵列，阵列响应向量由下式给出：

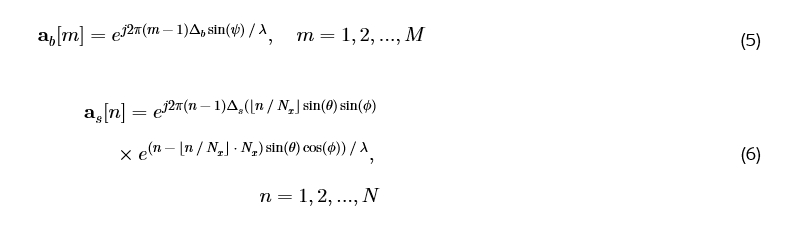
其中 Δ_b 和 Δ_s 分别是天线和元件间距，N_x 是 RIS 每行的元件数量。

​3.3 路径损耗模型​

我们采用 3GPP 规范 TR 38.901 [31] 的城市传播模型来求路径损耗 L。以 d 作为源和目的地之间的距离，载波频率 f_c，LoS 链路的路径损耗由下式给出

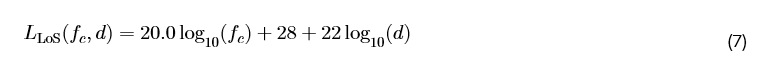
对于 NLoS 路径：

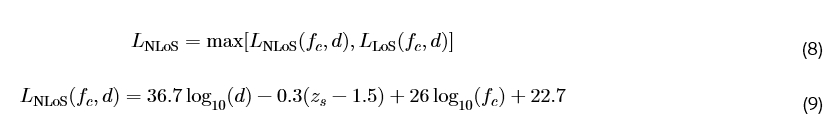
所有其他信道，即 H{b,t}^ℛ, H{b,t}^𝒯, H{s,t}^ℛ, H{s,t}^𝒯，被建模为瑞利衰落 (κ=0)，因为它们的 LoS 传播不能保证。

​3.4 信号模型​

BS 处的波束成形矩阵由 W_B(t) 给出。令 s_j(t) 和 v_j(t) ∈ ℂ^{M×1} 分别表示用户 j 在 BS 处的信息序列和主动波束成形向量。BS 在时隙 t 发射的信号为：

经过高斯噪声 n_0 后，到达 Aerial-STAR 的信号为：

反射用户 p 和透射用户 q 的接收信号为：

信干噪比（SINR），噪声功率为 σ²，对于单个用户由下式给出：

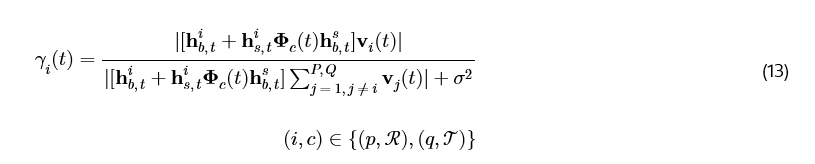
每个用户的数据速率为

其中 B 是系统带宽。

​3.5 Aerial-STAR 能量模型​

Aerial-STAR 能量消耗包括无人机推进所需的能量和克服 STAR-RIS 所经历阻力所需的能量。我们使用[32]提出的用于水平运动的无人机能量模型。无人机的总功耗 P_UAV 可以描述为：

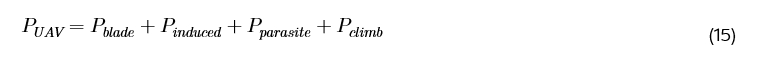
其中 P_blade 指的是叶片轮廓功率，用于补偿转子叶片中的粘性阻力损失，P_induced 是诱导功率，用于克服转子叶片上的诱导阻力所需的能量。此外，P_parasite 是克服无人机机身阻力所需的寄生功率，而 P_climb 是在爬升或下降过程中改变势能所需的功率。这些项的数学表示为：

在这些表达式中，ρ, δ, Ω, A, s, 和 r 分别代表空气密度、轮廓阻力系数、转子角速度、转子面积、实度（solidity）和转子半径。乘积 r Ω 代表叶片尖端速度。同时，V, T, v_i, 和 d_0 分别代表空速、推力、诱导速度和机身阻力系数。\dot{h} 是爬升或下降速率。应注意，对于恒定的爬升/下降速率，T 等于无人机的重量。

我们的模型通过特别纳入克服由 STAR-RIS 引起的阻力所需的能量，弥补了现有文献中的一个关键空白。在先前的研究中，当改变 RIS 元件数量来计算能量效率时，这个因素经常被忽略[33, 34, 35, 36]。

鉴于 RIS 工作在 f_c，波长是 λ = c / f_c。典型的 RIS 元件间距可以是 λ/μ，其中 μ ∈ (2,8) [37]。因此，对于一个每行有 N_x 个元件的方形 RIS，其表面积由下式给出

克服 RIS 阻力所需的功率为

其中 ρ 是空气密度，C_d 是 RIS 阻力系数（对于近方形表面通常为 2.1 [38]），V_⟂ 是速度垂直于 RIS 平面的分量。

那么时隙 t 的总功率由下式给出

系统在时隙 t 的通信效率定义为

通过纳入由 RIS 引起的阻力的能量消耗并使用详细的元件间间距模型，我们更准确地表示了 RIS 使能系统中的无人机能量动力学³。从这些方程中可以注意到，A_RIS 以及随之而来的 P_RIS-drag 随 N_x 呈二次方增长。因此，更多的 RIS 元件可能会导致更高的系统和速率，但由于更高的能量消耗，不一定能提高系统的能量效率，如图 2 所示。这个模型对于优化无人机-RIS 配置可能很有价值，并可以在解决实际部署挑战中发挥作用。

​3.6 问题表述​

我们的目标是通过联合优化无人机轨迹 T、STAR-RIS TRC 𝚽 和 BS 处的波束成形向量 W_B 来最大化系统的能量效率。该问题表述为

​​

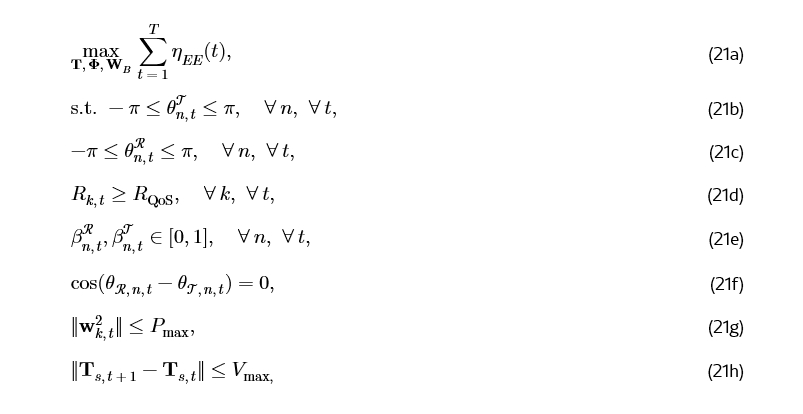
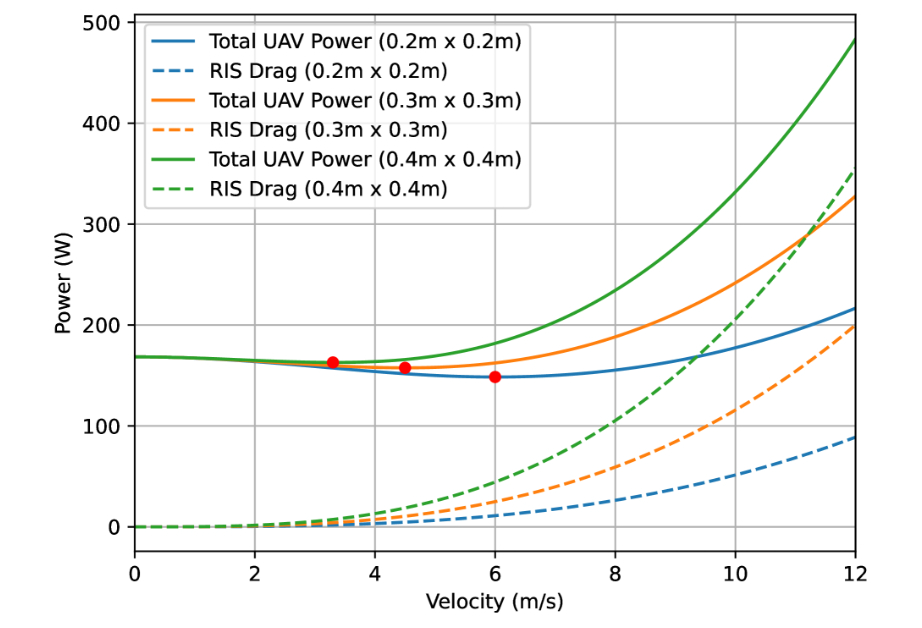
​图 2: 更大的 RIS 表面导致更高的阻力，特别是在更高速度下导致功耗增加，红色标记指示了每种情况下最节能的速度。该图表明，包含由 Aerial-STAR 引起的空气动力阻力非常重要，尤其是在面积和速度值较高时。​​

其中 (21a) 表示最大化能量效率的目标函数，(21b) 和 (21c) 是 TRC 相移的范围约束，(21d) 表示最低数据速率约束。(21e) 将幅度响应限制在合法范围内，(21f) 规定了透射和反射系数之间的耦合约束，(21g) 是最大功率约束，(21h) 约束了 Aerial-STAR 系统的最大速度。

应注意，耦合约束 (21f) 在联合优化 TRC 时增加了一层额外的挑战。该要求意味着只有一个，要么是 θ_n^ℛ 要么是 θ_n^𝒯，可以具有连续域。另一个将与第一个偏离 +π/2 或 -π/2。因此，相移的二元选择用离散动作而不是连续动作来处理可能更有效。

​4 提出的解决方案​

为了解决我们 STAR-RIS 系统中的优化挑战，我们在 DRL 框架内将问题表述为一个马尔可夫决策过程（MDP），从而能够应用深度强化学习技术。在这个表述中，每个时隙 t ∈ T 代表过程中的一个离散步骤。

​4.0.1 状态和动作​

在我们的案例中，智能体是一个网络控制器，可以放置在 Aerial-STAR 上以降低延迟并实时采取动作，或者可以是与 Aerial-STAR 有 LoS 链路的基站，这有助于减少 UAV 的计算量。智能体观察当前状态 s_t ∈ S，其中 S 表示状态空间。基于这个状态观察，智能体从动作空间 A 中选择一个动作 a_t ∈ A。对于每个 t，s_t 具有维度 (3 + 2 M N + 2 M J + 2 N J)，并包含关于 Aerial-STAR 位置和信道信息的信息，由下式给出：

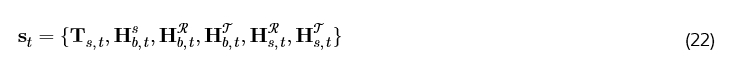
DA-DDPG 算法利用两个独立的 Actor 网络：一个用于连续动作，一个用于离散动作。这些网络并行运行，但通过评论家网络联合训练。状态被输入到连续和离散 Actor 网络，这些网络输出连续 (a_t^c) 和离散 (a_t^d) 动作：

分别是。a_t^c 的大小是 3 + 2 N + 2 M J，而 a_t^d 的大小是 N。

执行所选动作 a_t 后，系统根据底层信道动态和用户移动模式转换到新状态 s{t+1}。这个转换可以表示为元组 (s_t, a_t, r_t, s{t+1})，其中 r_t 表示作为动作结果收到的奖励。

​

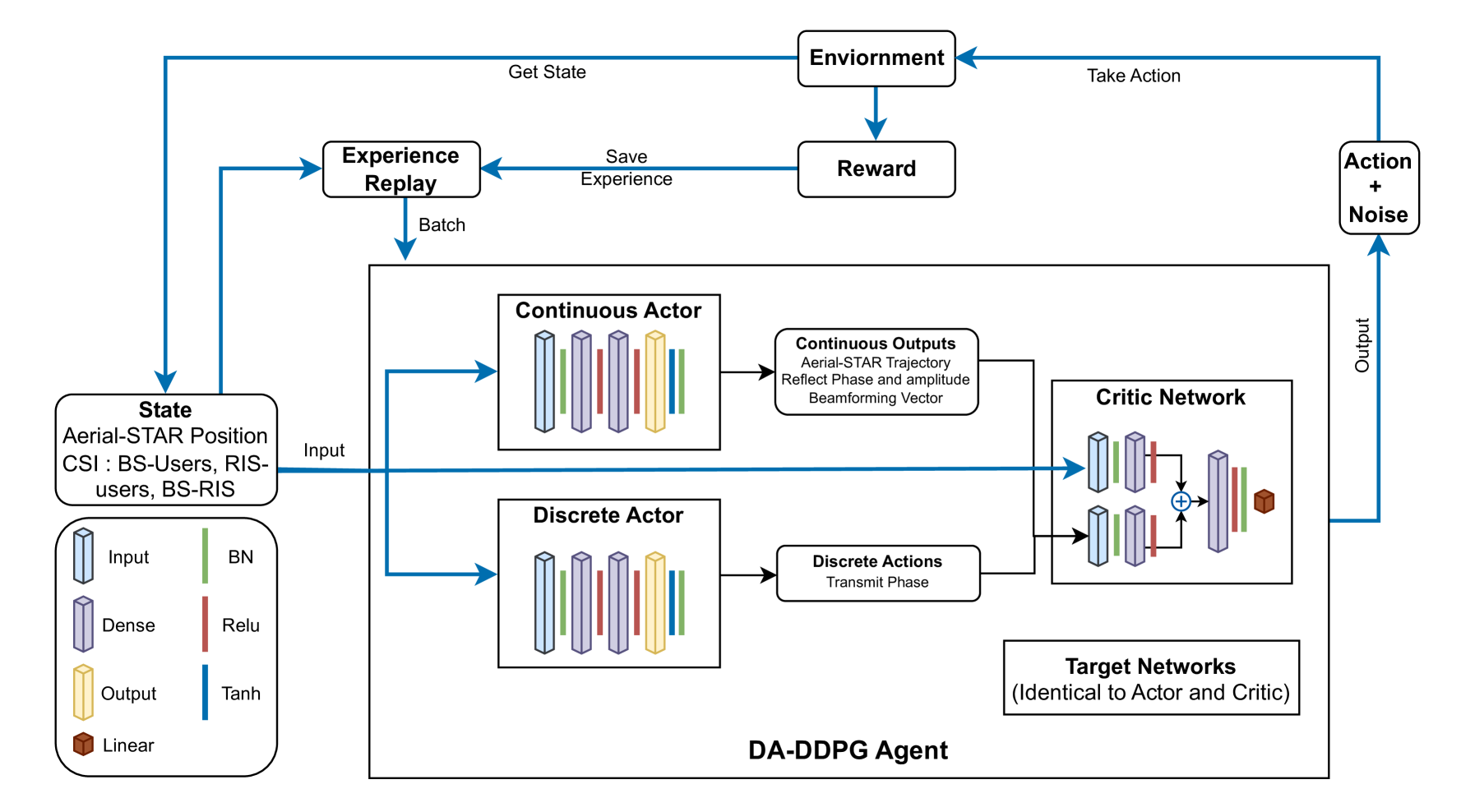
​图 3: 提出的 DA-DDPG 算法架构，具有用于连续和离散输出的独立 Actor 网络​

4.1 DA-DDPG 学习过程​

DA-DDPG 算法旨在最大化从每个状态 ​st开始的期望累积奖励。这是通过为每个状态 ​st确定最优动作 {at^c, ​at^d} 来实现的。具体来说，该算法寻求找到能最大化期望回报的动作，即从状态 ​st开始的折现未来奖励之和。数学上，目标是最大化价值函数 Q_μ( ​st, {at^c, ​at^d} )，它表示在状态 ​st下采取动作 {at^c, ​at^d} 并 thereafter 遵循最优策略的期望累积奖励，使用贝尔曼方程表示：

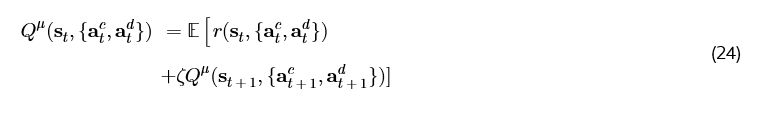
其中 ζ 是范围在 [0,1] 内的折扣因子，μ 代表将 ​st映射到 ​at的动作策略，r(⋅) 是收到的奖励。最优动作 ​at^* 表示为

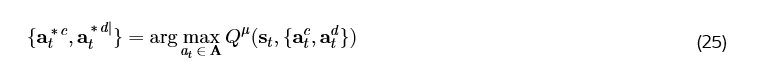
我们的方法使用两个参数化的 Actor 函数 μ_c( ​s​ | ω_μ^c ) 和 μ_d( ​s​ | ω_μ^d )，以及一个 Critic 函数近似器 Q( ​s, {ac, ​ad} | ω_Q )。我们通过最小化以下损失函数来训练 DA-DDPG 智能体：

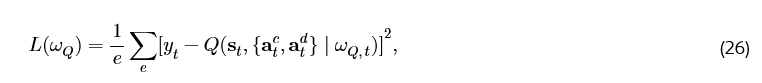
其中 L( ω_Q ) 是 Critic 网络的损失函数，ω_Q 是 Critic 网络的参数，e 代表采样的转移（transitions）数量。

目标 Q 值 y_t 由目标网络提供：

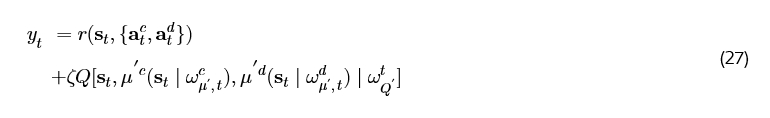
其中 ω_μ'^c, ω_μ'^d, ω_Q' 分别是连续和离散目标 Actor 网络以及 Critic 网络的参数。

我们使用从 Critic 网络导出的策略梯度来训练 Actor 网络，如 (28) 所示，其中 ∇{ω_μ^c} J 和 ∇{ω_μ^d} J 分别是连续 Actor μ_c 和离散 Actor μ_d 的策略梯度，​se 和 ​ae 代表从经验回放缓冲区中采样的状态和动作。

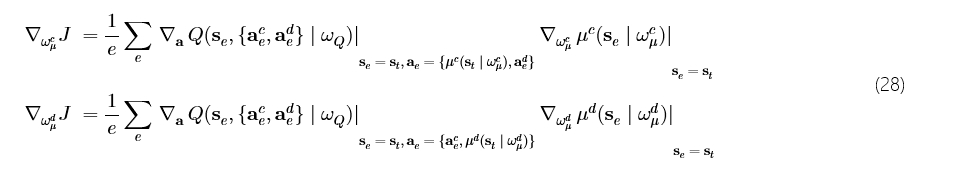
​4.2 动作空间与策略映射​

我们的连续 Actor 在时间 t 的动作表述为：

其中 𝒩OU( 0, σ^2 ) 是 OU 噪声 [39]，均值为 0，方差为 σ^2，被添加以鼓励在连续动作空间中进行探索。随着训练的进行，噪声会衰减以利于利用（exploitation）。然后，​at^c 被映射到智能体要执行的动作 (23a)。Aerial-STAR 轨迹包括 {V, θT, φT}，这是在约束 (21g) 下的行进距离，以及俯仰角和方位角上的运动角度，满足 -π/2 ≤ θT​ ≤ π/2 和 0 ≤ φT​ ≤ 2π。​at^{𝚽^ℛ}, ​at^{𝜷}, ​at^{wt} 中其他连续输出的映射分别按照 (21c), (21e) 和 (21g) 进行。

类似地，离散 Actor 策略输出动作，其中阈值处理过程将连续输出映射到离散值 [21]：

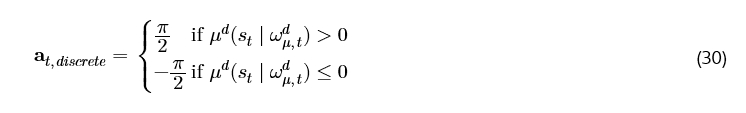
然后我们使用 epsilon-greedy 策略进行探索。

探索率 ϵ 随时间衰减，以在智能体学习时减少探索。那么，对于 STAR-RIS 元件 n，在时间 t 具有离散动作 a{n,t}^d ∈ ​at^d，有：

​4.3 奖励结构​

​4.3.1 通过基于调和公平指数（HFI）的奖励函数增强公平性​

在无线网络中，公平性度量通常用于衡量资源分配的均匀程度。最常用的度量是 Jain 公平指数（JFI），由 [40] 引入，其定义为：

然而，当用户吞吐量差异很大时，JFI 对公平性的敏感性有限。由于 JFI 依赖于算术平均，即使在用户之间存在显著性能差距的场景下，它也可能产生相对较高的公平性分数，这对于吞吐量较低的用户可能是不利的 [41]。在 RIS 辅助的网络中，由于障碍物、无人机距离和干扰等因素，用户吞吐量可能变化很大，JFI 对差异的宽容可能导致在具有挑战性条件下的用户的资源分配欠佳。

为了解决这些局限性，我们引入了调和公平指数（HFI）作为一种新颖的度量，用于评估资源分配中的公平性，特别是在无人机-RIS 辅助的网络中。调和平均数，作为毕达哥拉斯平均之一 [42]，计算为倒数之和的逆平均值。我们将 HFI 定义为用户吞吐量的调和平均数与算术平均数之比：

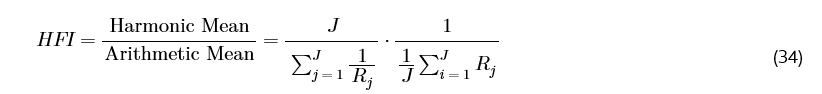
​4.3.2 HFI 与 JFI 的比较​

虽然 HFI 和 JFI 都提供了介于 0 和 1 之间的公平性度量（1 表示完全公平），但 HFI 对服务不足的用户提供了增强的敏感性。这是由于调和平均数的特性，即受数据集中较小值的强烈影响。JFI 在高吞吐量差异的场景中往往更宽容。

​

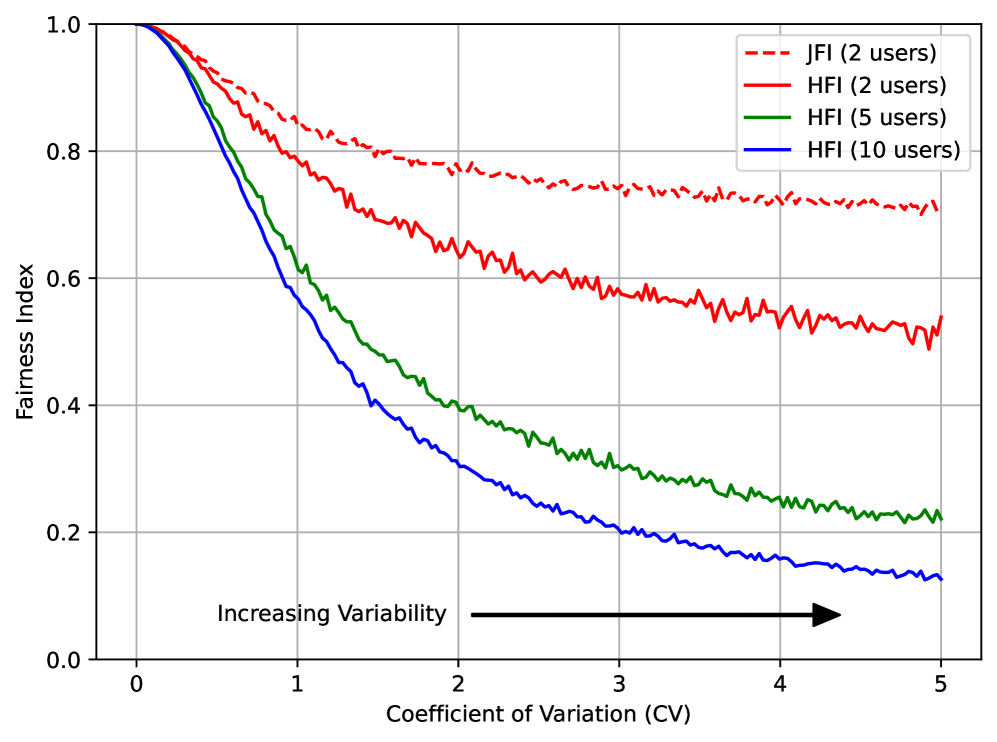
​图 4：HFI 和 JFI 随不同变异系数（CV）变化的比较。与 JFI 相比，HFI 对相同的用户输出更低的公平性指数。此外，对于相同的 CV，HFI 的惩罚随着用户数量的增加而增加。​​

图 4 说明了 HFI 和 JFI 在不同变异系数（CV）下的行为。CV 是吞吐量标准差与其均值的比率，这为我们提供了吞吐量差异的归一化度量。随着 CV 增加，两个指数都下降，但 HFI 表现出更陡峭的下降。这证明了 HFI 对吞吐量变化具有更高的敏感性，使其更适用于优先考虑所有用户最低数据速率的场景。HFI 的敏感性随着用户数量的增加而增加，促进了在更大网络中更公平的资源分配⁴。

在无人机-RIS 系统中，由于无人机距离、障碍物和干扰等因素，网络条件可能发生显著变化，HFI 增强的敏感性特别有益。将 HFI 纳入优化目标有助于在最大化总吞吐量的同时实现公平的资源分配。HFI 随着 CV 增加而迅速下降，鼓励在高差异场景中进行更积极的负载平衡和资源重新分配，从而产生更动态的无人机定位和 RIS 配置策略。这使 HFI 能够在整个网络中提供更公平的用户体验，如第 5 节所示。

我们无人机-RIS 系统的奖励函数旨在最大化用户公平性和总速率，并最小化总功耗。

其中 α 和 β 是缩放因子。第一项促进了用户间的公平性和高的总速率。通过将系统总速率与对低性能用户敏感的 HFI 相乘，我们确保系统不仅在每个时间间隔内最大化总数据传输量，而且 across all users 保持公平的服务（即保持可比的数据速率）。第二项引入了对过高功耗的惩罚，推动系统朝向节能运行。通过调整比率 β/α，我们可以微调公平性、总速率和能耗之间的权衡，允许灵活适应 Aerial-STAR 系统中的各种操作优先级和约束。在我们的实验中，我们选择 β/α 的值在 0.1-0.2 之间，以优先考虑更好的网络性能而不是节省能源。然而，最佳比率可能根据系统的特定场景（例如，用户的数量和分布、无人机能量约束）和优先级（数据速率与能量）而变化。

​4.4 DA-DDPG 架构​

DA-DDPG 网络的结构，包括两个 Actor 网络（连续和离散）和一个 Critic 网络，是根据问题表述（第 3 节）中讨论的离散和连续动作之间的耦合关系精心设计的。Actor 网络包括一个接受状态输入的输入层，带有批归一化（batch normalization），后面是密集层（dense layers），每个都使用 ReLU 激活函数。输出层使用 tanh 激活函数来产生连续动作。离散 Actor 网络与连续 Actor 具有相似的结构，但其输出层对应于离散动作的数量。Critic 网络的结构有两个输入分支：一个用于状态，一个用于动作，每个都有一个批归一化层，如图 3 所示。状态分支由密集层和 ReLU 激活组成。结合了连续和离散动作的动作输入通过一个具有 ReLU 激活的密集层。这些分支然后被连接（concatenated）起来，后面跟着具有 ReLU 激活的密集层。所有网络中隐藏层的大小是根据状态和动作的维度确定的，这可能因特定问题领域而异。

1 初始化环境

2 使用 Actor 网络 ω_μ^c, ω_μ^d, Critic 网络 ω_Q, 目标 Actor 网络 ω_μ'^c, ω_μ'^d, 目标 Critic 网络 ω_Q' 初始化 DA-DDPG

3 初始化经验回放

4 for episode=1 → 最大 episode 数 do

5 设置环境到 ​s_t=0

6 for t=0 → T do

7 观察 ​s_t

8 根据 (29), (23b) 选择动作 {at^c, ​at^d}

9 执行 {at^c, ​at^d}

10 观察 ​rt 和下一个状态 ​st+1

11 将转移（transition） {st, {at^c, ​at^d}, ​rt, ​s_t+1} 存储到经验回放中

12 从经验回放中随机采样转移 {se, {ae^c, ​ae^d}, ​re, ​s_e+1}

13 根据 (27) 设置目标

14 使用最小化损失 (26) 更新 Critic Q( ​s_t, ω_Q,t )

15

16 使用 (28) 更新 Actor 策略 μ_c( ​st, ω_μ,c^t ) 和 μ_d( ​st, ω_μ,d^t )

17 更新目标网络：ω_μ',t^i ← (1-τ) ω_μ',t^i + τ ω_μ',t^i, for i∈{c,d} 且 ω_Q't ← (1-τ) ω_Q't + τ ω_Q'_t

18

19 ​st ← ​st+1

20 end for

21

22 end for

​算法 1 DA-DDPG 算法​

​4.5 复杂度分析​

复杂度分析涉及计算通过这些网络一次前向传播所需的浮点运算次数。我们假设 Actor 和 Critic 网络有 I 层，每层有 θ_i 个节点。θ_t, θ_r 和 θ_b 分别表示 tanh、ReLU 和 BN（批归一化）层中的节点数，这些层分别需要 6、1 和 5 次浮点运算 [43]。我们的离散 Actor 的复杂度由下式给出：

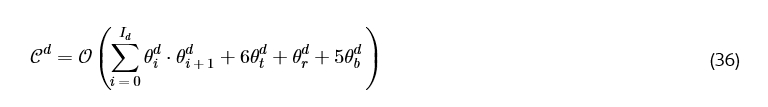
类似地，𝒞c 和 𝒞Q 分别表示连续 Actor 和 Critic 网络的复杂度。两个 Actor 接受相同的输入并且并行操作（独立的前向传播和梯度计算），因此复杂度由更复杂的网络主导。因此，双 Actor 的复杂度由 𝒪( max(𝒞c, 𝒞d) ) 给出。因此，总复杂度由 𝒪( max(𝒞c, 𝒞d) + 𝒞Q ) 给出。应注意，由于连续 Actor 网络的大动作空间，𝒞c 几乎总是高于 𝒞_d。

对于一个有 e 个训练周期（epoch）和 T 个时间步长的传输周期，总复杂度可以计算为：

应注意，在传统的 DDPG 中，使用单一网络，动作空间将包含所有 ​at^c + ​at^d 个动作。使用与 DA-DDPG 相同的 Actor 架构，传统 DDPG Actor 的复杂度会更高，因为 max( |ac|, |ad| ) ≤ ( |ac| + |ad| )。

​5 结果与分析​

我们在配备 3.2 GHz CPU、16 GB RAM、macOS Ventura 13.2.1 的 Apple M1 Pro 上进行仿真。TensorFlow 2.5 用于在具有 16 个核心的 M1 Pro GPU 上的 JupyterLab 中。我们假设用户随机分布在 ℛ 或 𝒯 区域。基站距离 Aerial-STAR 1 公里，Aerial-STAR 通过停留在 ℛ 和 𝒯 区域之间来操作。我们假设每个 episode 持续 30 秒，无线信道每秒更新一次。使用 Adam 优化器进行训练，默认学习率设置为 0.0001。Actor 网络有 2 个 ReLU 和 1 个 Tanh 激活函数，每个有 256-512 个神经元（取决于 RIS 元件数 N），而 Critic 网络有 3 个具有 ReLU 激活函数的密集层以及一个连接层（concatenation layer）。表 1 列出了所有重要参数的值。用于无人机参数的大多数符号和值参考自 [32, 44]。

​表 1：仿真参数​

参数	符号	数值	参数	符号	数值
载波频率	f_c	5 GHz	批量大小 (Batch size)	e	64
STAR RIS 元件数	N	16	总转子盘面积	A_r	0.503 m²
BS 天线数	M	4	叶片角速度	Ω	300 rad/sec
信道带宽	B	1 MHz	轮廓阻力系数	δ	0.012
用户数	J	4	机身阻力比	d_0	0.6
噪声功率谱密度	σ	-95 dBm/Hz	转子诱导速度	v_i	4.028 m/s
发射功率	P_max	29 dBm	转子实度	s	0.05
莱斯因子	κ	5	叶片尖端速度	r ⋅ Ω	120 m/s
QoS 要求	R_QoS	200 kb/s	Aerial-STAR 重量	W	25 N
学习率	lr	0.0005	空气密度	ρ	1.225 kg/m³
折扣因子	ζ	1	最大 Aerial-STAR 速度	V_max	10 m/s

​​

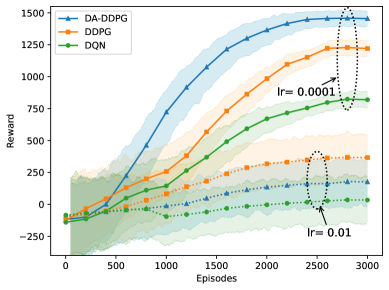
​图 5：在不同学习率设置下，DA-DDPG、DDPG 和 DQN 的比较奖励图。​​

​5.0.1 DA-DDPG 与相关 RL 算法的比较​

图 5 比较了三种不同 RL 解决方案在 3000 个 episode 中的奖励累积情况。选择 DDPG 和 DQN 作为基准，因为它们是基础性的，并且在文献中广泛用于优化 RIS 系数和无人机轨迹。对于学习率 0.0001，DA-DDPG 收集的奖励分别比 DDPG 和 DQN 高 24% 和 97%。标准的 DDPG 使用单一的 Actor 网络处理两种动作类型，性能明显优于 DQN，但效率低于 DA-DDPG。DDPG 具有与 DA-DDPG 相似的架构，但使用单一的 Actor 网络来处理离散和连续（阈值化后的）动作。虽然更简单的架构可能使其更容易训练，但 DDPG 难以处理混合动作空间的复杂性。DQN 仅限于离散输出，在三种算法中表现最差。这些改进突显了 DA-DDPG 分离的 Actor 网络方法在处理混合动作空间方面的显著优势，有效地平衡了连续和离散动作的学习。图 5 也说明了学习率的影响，lr=0.01 作为更大的步长，对于我们这个复杂的问题收敛到更低的奖励。

​

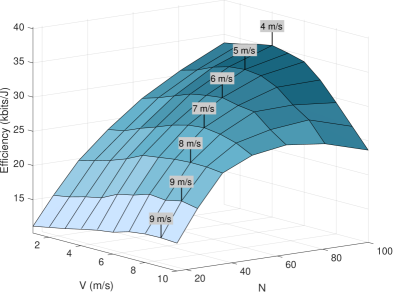
​图 6：通信效率随 Aerial-STAR 速度和元件数量的变化。​​

​5.0.2 STAR-RIS 尺寸与无人机速度的权衡​

图 6 揭示了 N（Aerial-STAR 的元件数量）、Aerial-STAR 在 3D 轨迹中的最大速度 V_max 与通信效率之间复杂的关系。该图表明，效率并不随 N 单调增加。在相同速度下，增加 N 会使效率先增加到最大值然后下降。这是因为，尽管吞吐量随着 RIS 元件数量的增加而增加，但 RIS 尺寸以及 consequently Aerial-STAR 系统所经历的阻力也增加（与天线尺寸的平方成正比 (18)），从而增加了功耗并降低了通信效率。该图还显示，随着 V_max 增加，最佳速度（对应于最大效率）出现在更低的 N 值。该分析展示了 N、V_max 和整体通信效率之间存在权衡，必须在设计时仔细考虑。

​5.0.3 部署策略比较​

图 7 描绘了各种 Aerial-STAR 部署策略的奖励收敛情况，而图 8 有助于根据用户移动可视化所有轨迹。3D 轨迹策略通过优化 2D 位置和高度，始终获得最高的奖励（比次优策略提高了约 28%），从而最大化吞吐量和公平性。最优 2D 轨迹策略表现出较低的性能，可能是由于增加了天线阻力而没有高度优化带来的增加吞吐量的好处。最优高度策略虽然能够调整高度，但无法优化 2D 位置，导致性能欠佳，原因是增加了垂直移动的功率，而没有水平重新定位以优化吞吐量的补偿效益。固定部署最初由于功耗较低而表现良好，但最终以最低的奖励水平收敛。这突显了节能与通过重新定位适应变化条件和优化吞吐量的能力之间的权衡。这些结果强调了在 Aerial-STAR 系统中 3D 定位的显著优势，其中每个自由度都有助于整体系统效率。

​

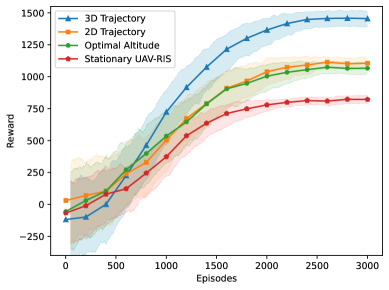
​图 7：不同 Aerial-STAR 轨迹的奖励。​​

​

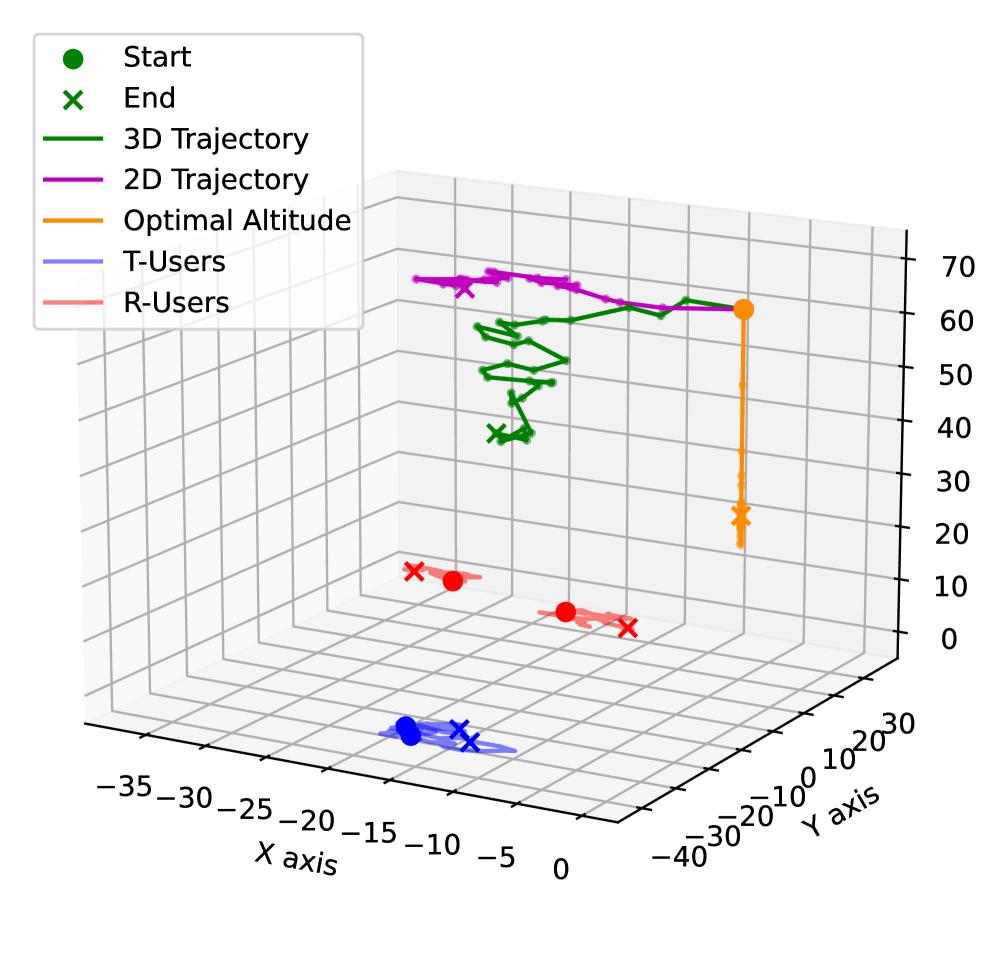
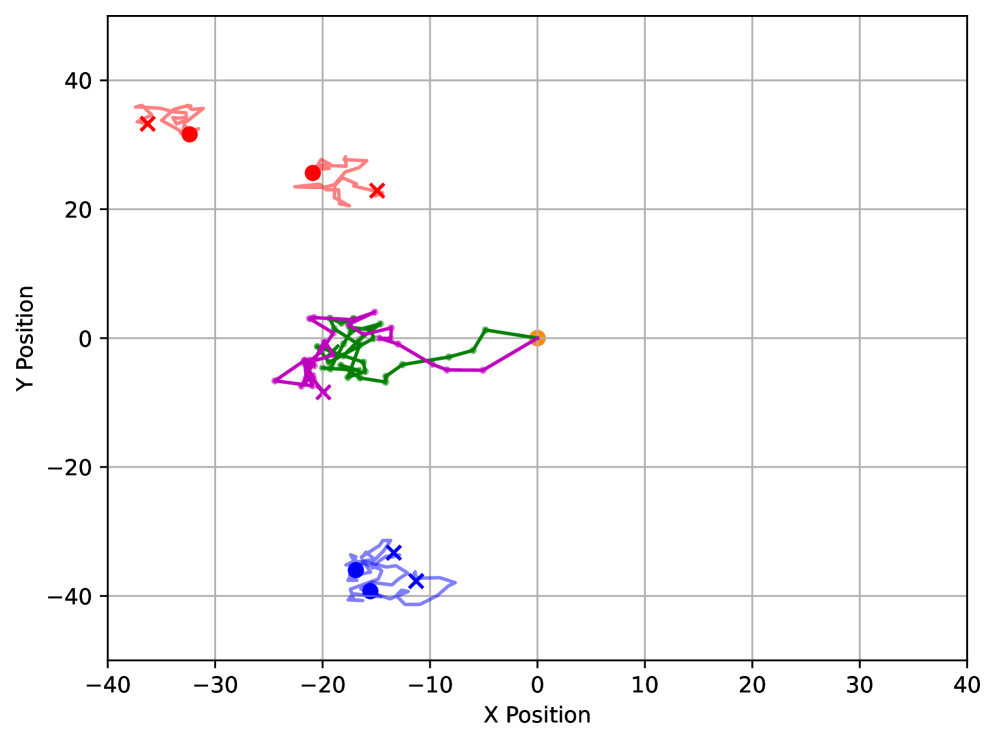
​​(a) 场景 1: 3D (右) 2D (左) 轨迹​

​​

 

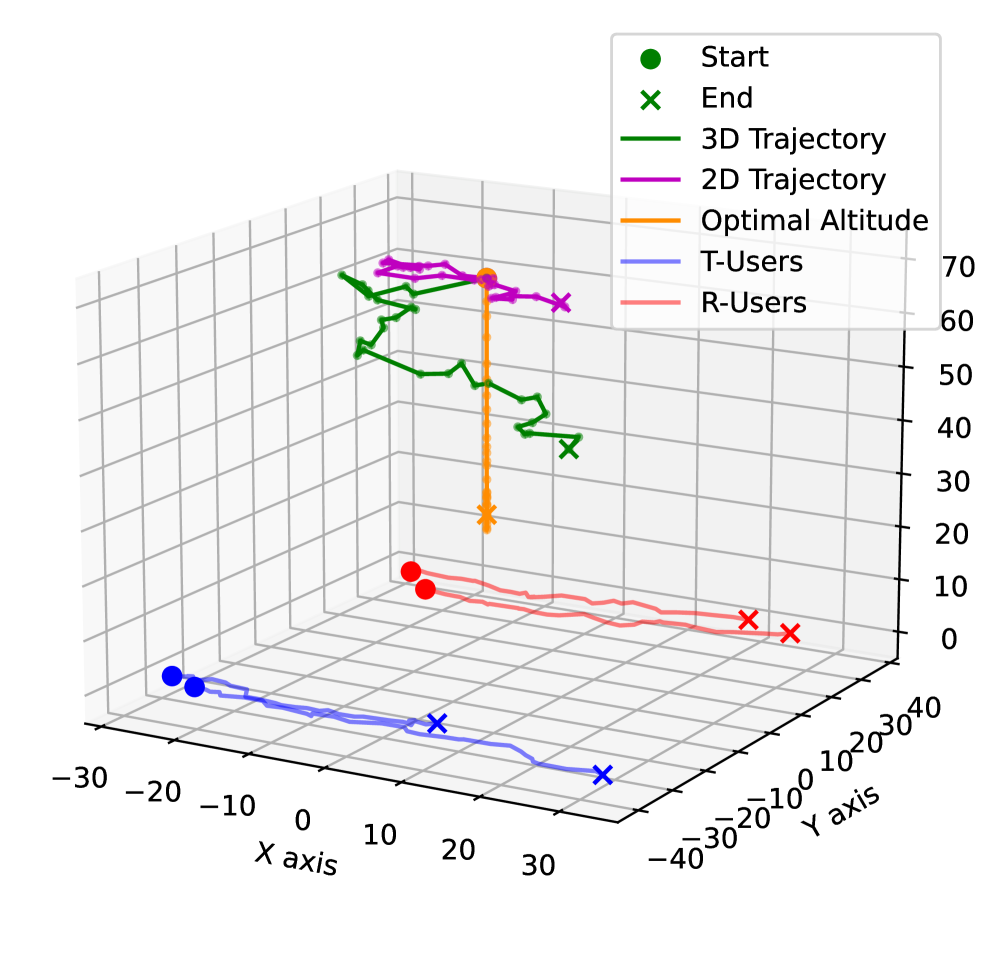
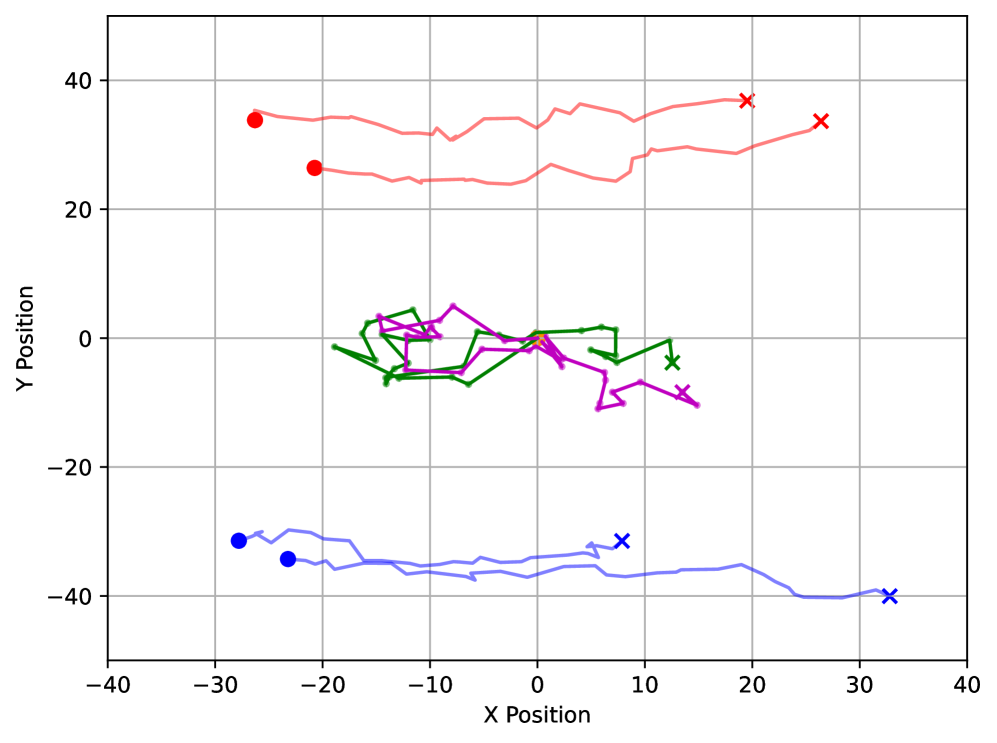
​​(b) 场景 2: 3D (右) 2D (左) 轨迹​

​图 8：在 3 种不同用户移动场景下 Aerial-Star 轨迹的可视化 - a) 随机移动和 b) 高度定向移动。可以观察到，3D 优化允许 Aerial-STAR 在 2D 平面上紧密跟随用户的大致移动方向，并优化高度，同时为 𝒯 和 ℛ 用户组保持最佳覆盖。​​

​

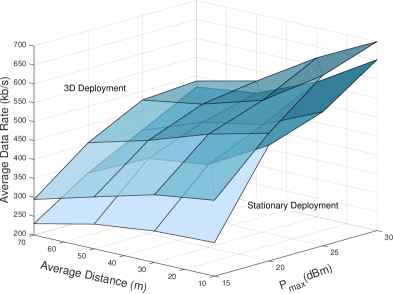
​图 9：不同 P_max 和 Aerial-STAR 与用户在水平面上平均距离下的每用户平均数据速率。​​

​5.0.4 发射功率和用户距离的影响​

图 9 揭示了搭载在无人机上的 STAR-RIS 与其固定部署的对应方案在变化的 P_max 和 STAR-RIS 与用户之间的平均距离下的通信性能差异。尽管图 7 已经讨论了 3D 部署在奖励累积方面的优越性，但重要的是要注意奖励函数包含了无人机功耗。实际上，固定的 STAR-RIS 很可能安装在固定架构上，因此有必要将其与无人机功耗脱钩。我们的分析强调了奖励改进中有多少可归因于卓越的通信性能。在用户距离和基站最大发射功率的各种场景下，3D 部署由于其能够在三维空间中优化位置而始终优于固定部署。对于增加的 P_max 和平均距离值，3D 部署保持其优越性。对于最低距离和功率组合，3D 部署的性能比固定部署高 38%。应注意，这种性能差距在更高功率和更大距离下会缩小——对于最高距离和功率组合，仅缩小到 4%。在后一种场景中，Aerial-STAR 微小位置调整的影响相对于较大的用户-无人机距离变得不那么明显，高度优化成为主要区别因素。此外，随着发射功率增加，固定部署 RIS 的扩展范围进一步最小化了两种方法之间的性能差异。可以得出结论，Aerial-STAR 部署可能优于固定部署，特别是当 ℛ 和 𝒯 区域的用户距离不是非常远时。

​

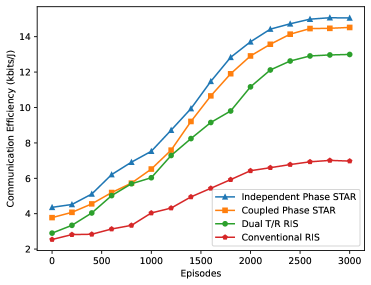
​图 10：STAR-RIS、双 T/R RIS 和传统反射 RIS 训练时的通信效率图。​​

​5.0.5 采用各种 STAR-RIS 类型的 Aerial-STAR 性能​

各种 RIS 方案的比较如图 10 所示。独立相位 STAR RIS 作为理想场景，由于后者在相位控制方面的实际限制，以微小优势优于耦合相位 STAR RIS。然而，耦合相位 STAR RIS 显示出比双 T/R RIS 有 22% 的改进，这得益于它能够同时服务 𝒯 和 ℛ 用户。相比之下，双 T/R RIS 被配置为 2 个 RIS，每个服务 ℛ 和 𝒯 区域，元件总数与 Aerial-STAR 相同以进行公平比较。双 T/R RIS 作为一个‘模式切换’RIS，具有固定的 T/R 元件比率，缺乏 STAR-RIS 的灵活性，使得 STAR-RIS 在动态环境中更有效。传统的仅反射 RIS 仅支持 ℛ 用户，无法协助另一侧的 𝒯 用户，导致效率最低。

​5.0.6 将 HFI 加入奖励函数的效果​

将公平性指数纳入奖励函数的影响如图 11 所示。它比较了不同奖励公式下的最低数据速率 QoS 约束违反率。图表显示，基于 HFI 和 JFI 的奖励都显著优于没有考虑公平性的基线奖励。值得注意的是，基于 HFI 的奖励始终实现最低的 QoS 约束违反率，在前 500 个 episode 内迅速下降到 0.10 以下，并且与基于 JFI 的奖励函数相比，最终改进了 41%。这是因为在高用户数据速率差异的场景中，HFI 比 JFI 施加了更高的惩罚，JFI 显示出类似的趋势但始终保持略高的违反率。这些结果强调了在奖励函数中纳入公平性度量的有效性。我们证明 HFI 能够以最低数据速率 QoS 约束服务更多用户，从而在所有用户中带来更一致的网络性能。

​

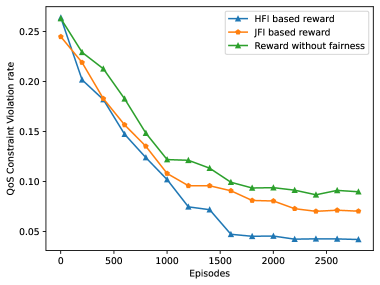
​图 11：比较 HFI 和 JFI 的最低数据速率 QOS 违反率图。​​

​6 结论​

本研究分析了在无人机上部署耦合相移模型的 STAR RIS 对下行链路通信的影响。优化无人机轨迹、基站波束成形向量和耦合的 TRC 是一个具有挑战性的问题，因为它需要离散和连续值的输出。为此，我们提出了一种 DA-DDPG 算法，该算法具有两个 Actor 网络（分别用于离散和连续动作）以优化 Aerial-STAR 系统的通信效率。我们还提出了一种新的调和公平指数（HFI），并表明将其纳入我们的奖励函数可以提高用户间的公平性。结果表明：1) DA-DDPG 的性能分别优于 DDPG 和 DQN 算法 24% 和 97%，2) 3D 部署在其他部署策略中产生最高的奖励，3) 耦合相位 STAR 的性能优于双 T/R RIS 和传统 RIS，4) 增加无人机部署的 RIS 中的元件数量不一定会提高通信效率。

在未来网络（设想如图 12 所示）中，多个第三方 Aerial-STAR 可以同时提供服务，基站独立运营。这种场景需要在服务之间建立稳健的握手机制，这与欧盟 6G 研究计划 Hexa-X [45] 和 Next G Alliance 的“6G 路线图”[46] 报告中强调的作为未来网络架构关键推动因素的 Open RAN 概念相一致。在这种设置中，扩展版本的 DA-DDPG 智能体可以集成到与 Open RAN 兼容的基站架构中，例如爱立信的 Cloud RAN 解决方案，该方案预计将支持 O-RAN 前传接口 [47]。基站可以通过管理更广泛的 Aerial-STAR 定位来提供高级控制，通过标准化的 Open RAN 接口最大化覆盖范围，而每个无人机集群的低级控制可以由专有的第三方软件在本地管理。这些原则也反映在 3GPP 的技术报告 TR 38.801 [48] 中，该报告概述了支持无线接入网中功能分割的架构。这种分层方法使得在一个开放的多供应商生态系统内能够进行灵活且稳健的网络优化，允许高效协调多个 Aerial-STAR 系统。

​

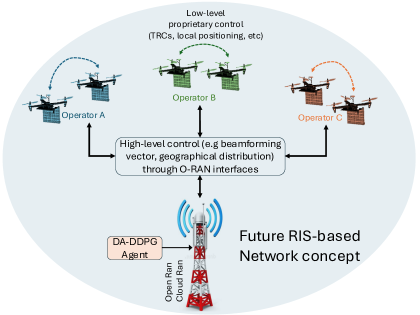
​图 12：促进多供应商 Aerial-RIS 使能网络的 Open Ran 操作模型。​