智能优化算法（源码）-沙丘猫群优化（SCSO）

获取更多资讯，赶快关注上面的公众号吧！

沙丘猫群优化算法（Sand Cat swarm optimization，SCSO）是土耳其学者Amir Seyyedabbasi于2022年最新提出的一种模拟沙丘猫生存行为的元启发式算法。扫码关注公众号，后台回复"沙丘猫"或"SCSO"获取源码和原文。

灵感来源

沙丘猫是猫科动物中的一种，属于哺乳动物家族。它们生活在沙质和石质沙漠的恶劣环境中，如中亚撒哈拉沙漠、非洲撒哈拉沙漠和阿拉伯半岛。沙丘猫虽然和家猫在外形上差别不断，但在捕食和生存方面有着不同的生活行为。它们能够探测低于2kHz的低频，也具有难以置信的挖掘猎物的能力。作者提出的沙丘猫算法就是受这两种特性的启发，也包括两个阶段：搜索和攻击，此外，还提出一种用于平衡探索和利用的机制。

数学模型和优化算法

沙丘猫群优化模拟了沙丘猫的两个主要行为：搜寻猎物和攻击猎物。由于自然界中的沙丘猫是独立生活的，那么在提出的算法中，为了提出种群智能的概念，作者假设沙丘猫是群体性的。

初始化种群

对于$d$维优化问题，沙丘猫就是一个$1\times d$维的表达问题解的数组，如图2。

每个变量值$\left(x_1,x_2,\dots ,x_d\right)$都是浮点型，且每个$x$都必须处于上下边界之间（$\forall x_i\in [$ lower, upper $]$）。

算法运行时首先根据问题的规模$\left(N_{\text{pop }}\times N_d\right),($ pop $=1,...,n$)利用沙丘猫群创建一个候选矩阵，然后就目标函数对每个沙丘猫进行适应度评估，选择出其中最优的个体，其他的个体都朝向该个体移动。

搜索猎物（探索）

沙丘猫的猎物搜索机制依赖于低频噪声发射。每只沙丘猫的解表达为$X_i=\left(x_{i1},x_{i2},x_{i3},\dots ,x_{id}\right)$。SCSO算法得益于沙丘猫在低频探测方面的听觉能力，这样就声明了每只猫的敏感范围，前面提到，沙丘猫可以感知低于2kHz的低频，在数学模型中，根据算法的工作原理，这个值（$\overrightarrow{r_G}$）将随着迭代过程的进行从2线性地降低为0，以逐渐靠近猎物而不会丢失或跳过。因此为了搜索猎物，假设沙丘猫的敏感范围为2kHz到0（等式1），$S_M$模拟了沙丘猫的听觉特性，其假设为2（当然对于不同问题可以适当调整以确定代理行为的速度）。值得一提的是，控制探索和利用之间转换的主要参数是$R$,其是根据等式2获得的向量。
$$\overrightarrow{r_G}=s_M-\left(\frac{2\times S_M\times {\text{ iter }}_{\mathrm{c}}}{{\text{ iter }}_{\mathrm{M}\mathrm{a}\mathrm{x}}+{\text{ iter }}_{\max }}\right)\text{\hspace{1em}(1)}$$

$$\vec{R}=2\times \overrightarrow{r_G}\times \mathrm{rand}(0,1)-\overrightarrow{r_G}\text{\hspace{1em}(2)}$$
搜索空间在定义的边界之间随机初始化。在搜索步骤中，每个当前搜索代理的位置更新都是基于一个随机位置。这样，搜索代理就能够在搜索空间中探索新的空间。为避免陷入局部最优，每只沙丘猫的灵敏度范围是不同的，如等式3。因此，$\overrightarrow{r_G}$表示常规的灵敏度范围（从2线性下降到0），而$\vec{r}$是每只猫的灵敏度范围。此外，$\vec{r}$用于探索或利用阶段的操作，而$\overrightarrow{r_G}$用于导引参数$R$以实现在这些阶段间转移控制。

$$\vec{r}=\overrightarrow{r_G}\times \mathrm{rand}(0,1)\text{\hspace{1em}(3)}$$

其中${\text{ iter }}_{\mathrm{c}}$为当前迭代，${\text{ iter }}_{\mathrm{M}\mathrm{a}\mathrm{x}}$为最大迭代次数。

每只沙丘猫会根据最优解（$\overrightarrow{{\mathrm{Pos}}_{bc}}$）、自己当前位置（$\overrightarrow{{\mathrm{Pos}}_c}$）和其灵敏度范围（$\overrightarrow{r}$）更新自己的位置。因此沙丘猫能找到其他最好的猎物位置（等式4），该等式使得算法可以找到新的局部最优，因此新的位置位于当前位置和猎物位置之间，同时随机性保证了算法的运行成本低和复杂度低。

$$\overrightarrow{\mathrm{Pos}}(t+1)=\vec{r}\cdot \left(\overrightarrow{{\mathrm{Pos}}_{bc}}(t)-\mathrm{rand}(0,1)\cdot \overrightarrow{{\mathrm{Pos}}_c}(\mathrm{t})\right)\text{\hspace{1em}(4)}$$

攻击猎物（利用）

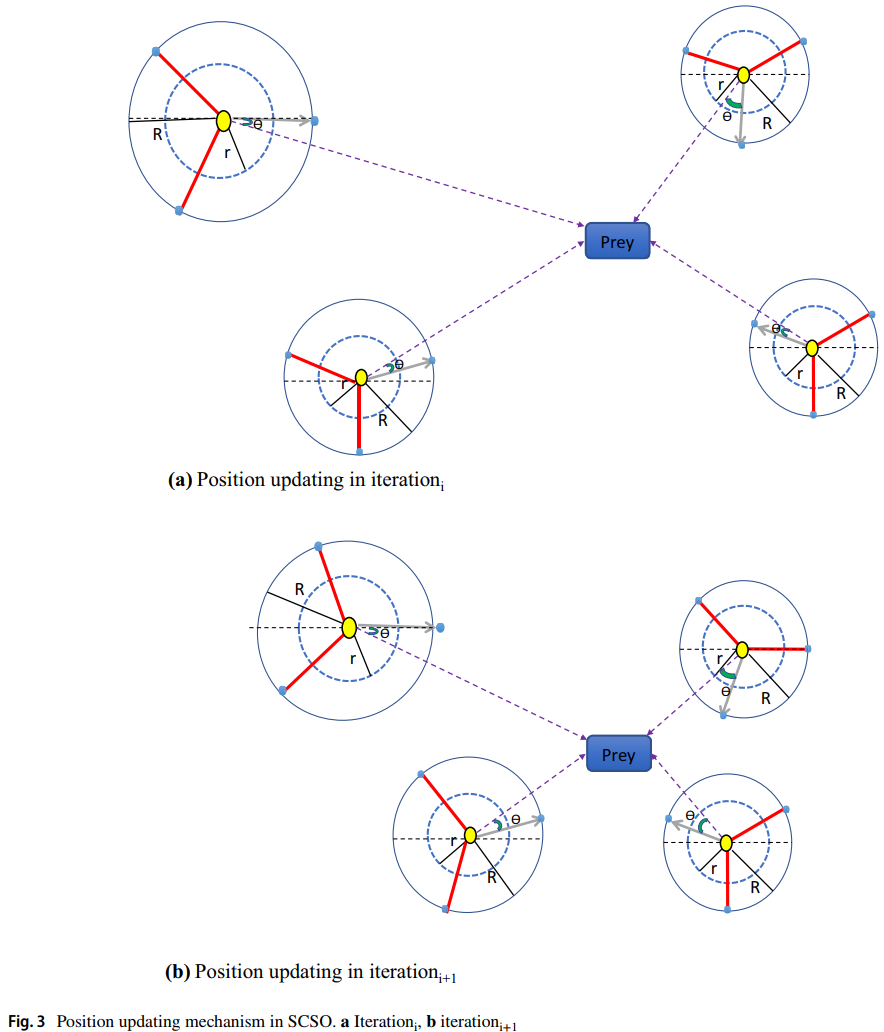
为了表达SCSO的攻击阶段，最优位置$\overrightarrow{{\mathrm{Pos}}_b}$与当前位置（$\overrightarrow{{\mathrm{Pos}}_c}$）的距离根据等式5计算得到。同时假设沙丘猫的灵敏度范围是一个圆，这样移动的方向就可以通过圆上的一个随机角度（$\theta$）确定。由于所选的随机角度在0到360之间，其值将在−1到1之间。这样，群体中的每个成员都能够在搜索空间中沿着不同的圆周方向移动。SCSO利用轮盘选择算法为每只沙丘猫选择一个随机角度。用这种方法，沙丘猫可以接近狩猎位置，为避免陷入局部最优，采用了随机角度。SCSO两次连续迭代的位置更新过程如图3所示。

$$\begin{array}{rl}& \overrightarrow{{\mathrm{Pos}}_{\mathrm{r}\mathrm{n}\mathrm{d}}}=\left|\mathrm{rand}(0,1)\cdot \overrightarrow{{\mathrm{Pos}}_b}(t)-\overrightarrow{{\mathrm{Pos}}_c}(\mathrm{t})\right|\\ & \overrightarrow{\mathrm{Pos}}(t+1)=\overrightarrow{{\mathrm{Pos}}_b}(t)-\vec{r}\cdot \overrightarrow{{\mathrm{Pos}}_{\mathrm{r}\mathrm{n}\mathrm{d}}}\cdot \cos (\theta )\end{array}\text{\hspace{1em}(5)}$$

探索和利用

探索和利用是通过自适应的$r_G$和$R$保证的，这些参数允许SCSO在两个阶段之间无缝切换。由于参数$R$取决于$r_G$,其波动范围也会变小。$R$是区间$[-2r_G,2r_G]$的随机值，而$r_G$线性从2下降到0。当R的随机值为[-1,1]时，沙丘猫的下一个位置可以是当前位置与狩猎位置之间的任意位置。SCSO算法在$R$小于或等于1时强制搜索代理进行利用，否则强制搜索代理进行探索和寻找猎物，如等式6。

$$\vec{X}(t+1)=\{\begin{array}{cl}\overrightarrow{{\mathrm{Pos}}_b}(t)-\overrightarrow{{\mathrm{Pos}}_{\text{rnd }}}\cdot \cos (\theta )\cdot \vec{r}& |R|\le 1;\text{ exploitation }\\ \vec{r}\cdot \left(\overrightarrow{{\mathrm{Pos}}_{bc}}(t)-\mathrm{rand}(0,1)\cdot \overrightarrow{{\mathrm{Pos}}_c}(\mathrm{t})\right)& |R|>1;\text{ exploration }\end{array}\text{\hspace{1em}(6)}$$

SCSO算法